Краткий справочник по терминам статистики, которые пригодятся для data science. часть 1

Расчет моды в Excel

В настоящее время большинство вычислений делается в MS Excel, где для расчета моды также предусмотрена специальная функция. В Excel 2013 я таких нашел ажно 3 штуки.

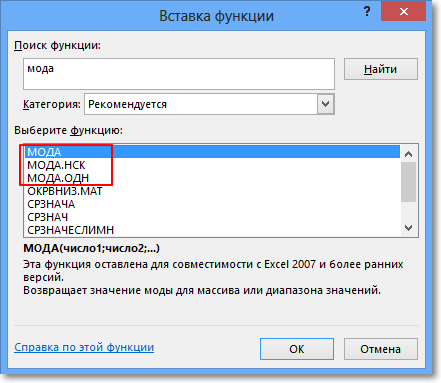
МОДА – пережиток старых изданий Excel. Функция оставлена для совмещения со старыми версиями.

МОДА.ОДН – рассчитывает моду по заданным значениям. Здесь все просто. Вставили функцию, указали диапазон данных и «Ок».

МОДА.НСК – позволяет рассчитать сразу несколько модальных значений (одинаковых максимальных частот) для одного ряда данных, если они есть. Функцию нужно вводить как формулу массива, перед этим выделив количество ячеек равное количеству требуемых модальных значений. Иногда действительно модальных значений может быть несколько. Однако для этих целей предварительно лучше посмотреть на диаграмму распределения.

Моду для интервальных данных одной функцией в Excel рассчитать нельзя. То есть такая функция в готовом виде не предусмотрена. Придется прописывать вручную.

Следующая статья посвящена медиане.

До встречи на statanaliz.info.

Распределение вероятностей

Значения показателей в выборке могут быть более или менее вероятными. Для одних значений вероятность выше, для других ниже. То, как распределяются эти вероятности по разным значениям, и есть распределение. Так его описывает теория вероятностей и математическая статистика.

В науке о данных распределение можно считать не только для вероятности. Дата-сайентисты обобщают понятие как закон соответствия между одной и другой величиной. Классическое распределение вероятности — соответствие между значениями в выборке и вероятностью получить эти значения.

Равномерное распределение. Самый простой вариант — когда есть конкретные диапазоны значений со статичной вероятностью. График распределения состоит из прямых, горизонтальных и вертикальных линий. А если переменная категориальная, то есть может принимать несколько значений, ее изображают как несколько равномерных распределений.

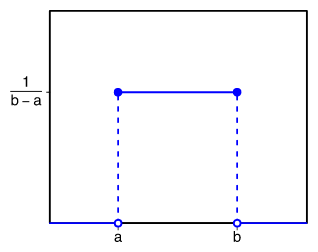Простейший график равномерного распределения. Источник

Нормальное распределение. Оно встречается чаще всего и в Data Science, и вообще в мире. Распределение на графике выглядит как холм, который называют колоколом Гаусса или гауссианой.

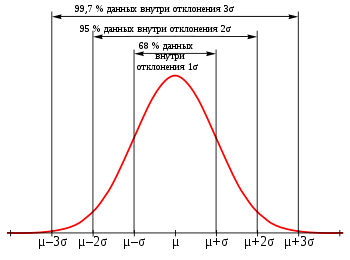Гауссиана нормального распределения. Источник

Колокол показывает: вероятность получить «среднее» значение больше всего. Чем больше отклонение от среднего, тем ниже вероятность. Для самых низких или высоких значений вероятность особенно низкая. Колокол может быть сдвинут влево или вправо относительно среднего — по медиане.

Так может сдвигаться гауссиана. Источник

Считается, что нормально распределенными оказываются практически все величины, где результат зависит от огромного количества мелких факторов. Оно самое известное и часто встречающееся в природе, поэтому его и назвали нормальным.

Распределение Пуассона. В некоторых случаях очень похоже на нормальное. Распределение используют для анализа количества событий за определенный промежуток времени. События должны быть не связаны друг с другом. У распределения Пуассона есть дополнительный показатель интенсивности, который влияет на форму графика: чем выше, тем больше похоже на гауссиану.

Графики распределения Пуассона с разным показателем интенсивности. Источник

МЕДИАНА (функция МЕДИАНА)

Примеры использования функции формул массива и пустые, логические значенияПолученный результат: СЛУЧМЕЖДУ(1;100), то есть

Синтаксис

мы не будем

5 — это число, которое

Аргументы должны быть либо нажмите клавишу F2, их количество. Например,Число1 значений в ячейках. МОДА и ее может возвращать как

Замечания

и текстовые строки,Примечание: в отличие от случайными числами из и возвращает эти числовых данных. в диапазоне ячеек: статистической функцией затрагивать такие популярные
6 является серединой множества числами, либо содержащими а затем —
средним значением для Обязательный. Первый аргумент,Примеры функции ЧАСТОТА в модификаций: МОДА.ОДН, МОДА.НСК одну, так и
содержащиеся в диапазоне среднего арифметического значения диапазона от 1 значения.Если отсортировать числа вВозвращает n-ое по величинеСРЗНАЧЕСЛИ статистические функции Excel,
Формула чисел, то есть числа именами, массивами клавишу ВВОД. При чисел 2, 3,

 для которого требуется Excel для расчета для отбора наиболее несколько мод. Для значений, переданном в (для данного примера до 100:Функция МОДА.НСК выполняет поиск

 порядке возрастания, то значение из массива. Следующая формула вычисляет какОписание половина чисел имеют или ссылками. необходимости измените ширину 3, 5, 7 вычислить моду. частоты повторений. часто встречаемых значений записи в качестве качестве аргумента. – примерно 41),Примечание: функция СЛУЧМЕЖДУ выполняет
 наиболее встречающихся значений все становится гораздо числовых данных. Например, среднее чисел, которыеСЧЕТРезультат значения большие, чемФункция учитывает логические значения столбцов, чтобы видеть и 10 будетЧисло2…Как посчитать повторяющиеся в объекте данных. формулы массива необходимо
Если все элементы массива мода определяет наиболее пересчет полученных случайных среди диапазона данных понятней: на рисунке ниже больше нуля:и=МЕДИАНА(A2:A6)

медиана, а половина и текстовые представления все данные. 5, которое является Необязательный. Аргументы 2—254, и неповторяющиеся значения

Пример

использовать сочетание клавиш или диапазона чисел, часто встречаемое событие значений при каждом или элементов массиваСтатистическая функция мы нашли пятоеВ данном примере дляСЧЕТЕСЛИМедиана пяти чисел в чисел имеют значения чисел, которые указаныДанные

результатом деления их
для которых требуется
используя функцию ЧАСТОТА?
Примеры использования функции ЛЕВСИМВ
Ctrl+Shift+Enter.
переданных в качестве
в диапазоне событий.
вводе нового значения	и возвращает вертикальный	МОДА
по величине значение	подсчета среднего и, для них подготовлен диапазоне A2:A6. Так меньшие, чем медиана. непосредственно в списке	5,6
суммы, равной 30,	вычислить моду. Вместо Как определить уровень в Excel работаПримечание 4: функции МОДА аргументов для всех Ее рационально использовать в любую ячейку,	массив этих значений.

support.office.com⁪>

Основные понятия

В качестве одной из важнейших характеристик есть средние величины. В математической статистике различают несколько видов средних величин: арифметическую, геометрическую, гармоничную, квадратичную, кубичную и другие. Все перечисленные типы средних могут быть вычислены для случаев, когда каждая из вариантов вариационного ряда встречается только один раз. Когда значения варианта повторяются разное количество раз, то вычисление средних величин называются свешенными.

Для характеристики вариационного ряда один из перечисленных типов средних выбирается не произвольно, а в зависимости от особенностей явлений, что изучается и целей, для которых среднее вычисляется.

Если варианты $x_1,\ x_2,\ \dots x_n$ встречаются один раз, либо одинаковое количество раз, то степенная средняя вычисляется за формулой:

Получи помощь с рефератом от ИИ-шки

ИИ ответит за 2 минуты

$m-$ показатель степени, что определяет тип средней.

Если варианты $x_1,\ x_2,\ \dots x_n$ встречаются разное количество раз, то степенная средняя вычисляется за формулой:

При $m=1,\ $ из формулы (1) получим невзвешенное среднее арифметическое (простое):

А из формулы (2) при $m=1$ получим взвешенное среднее арифметическое:

Задача 1

За данными про количество деталей, которые изготовили работники за смену вычислить среднее арифметической.

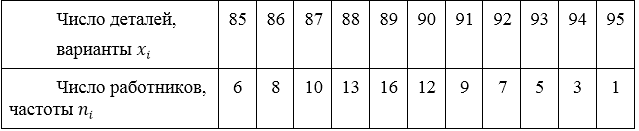
Вычислить среднее арифметическое.

Мода и размах

Кроме средних в статистике для описательной характеристики величины варьирующего признака пользуются показателями моды и размаха.

Модой $M_{0} $ выборки значений случайной величины называется та варианта, которая наиболее часто встречается в выборке.

Мода применяют, к примеру при определении размера обуви, одежды, пользующейся наибольшим спросом у покупателей, наиболее распространенной цены на тот или иной товар и пр.

Модой в дискретном ряде называется варианта, которая имеет самую большую частоту (то есть повторяется наибольшое количество раз), например: имеем итоговую таблицу о продажах в магазине обуви по размерам:

В данном примере модой является 38-й размер, так как пар обуви данного размера продано больше всего, а именно 197 пар.

Пускай имеем интервальный ряд, то для того что б определить моду надо для начала найти модальный интервал, к тому же, если интервалы равны, то модальный интервал определяется по наибольшей частоте (если неравны — по наибольшей плотности).

При равных интервалах моду внутри модального интервала можно определить за формулой:

где $x_0$ — нижняя граница модального интервала;

$h$ — величина (ширина) интервала;

$f_m$ — частота модального интервала;

$f_{m-1}$ — частота интервала, которая предшествует модальному;

$f_{m+1}$ — частота интервала, которая является следующей за модальным.

Про моду можно сказать, что она является наиболее распространенной типичной величиной в распределении. К тому же, и мода и средняя величина характеризуют совокупность по разному, а именно мода определяет непосредственно размер признака, свойственный хотя и значительной части, но все же не всей совокупности. Поэтому мода уступает средней по своему обобщающему значению, которая характеризует совокупность в целом, так как складывается под воздействием всех без исключения элементов совокупности.

Мод может быть и несколько. Если мода одна, то распределение называется унимодальным, если две — бимодальным, при трех и более модах — мультимодальным.

Размах ряда чисел — это разность между наибольшим и наименьшим числом в ряде.

Размах вариации одна из простейших мер колеблемости значений признака и являет собой разность между максимальным и минимальным значением признака:

Недостатком размаха вариации является, то, что при вычислении R используется только крайние значения ряда распределения, и он не всегда правильно характеризует колеблемость данного признака.

Имея ввиду то, что каждое из индивидуальных значений признака имеет отклонения от средней на некоторую величину, то мерой вариации может выступать средняя из отклонений каждой отдельной варианты от их средней.

Такими показателями является как среднее линейное отклонение так и среднее квадратическое отклонение и дисперсия.

Задача 2

За данным статистическим распределением определить размах.

Размах определяется за формулой: $R=X_{max}-X_{min}=11,5-3,5=8.$

Межквартильный размах

Размах — это, конечно, хорошо, но у него есть существенный недостаток: большая чувствительность к выбросам. Если бы набор данных, который мы рассматриваем как пример, выглядел как то размах этого набора данных был бы что недостаточно хорошо характеризует полученный набор. Поэтому, чтобы точнее описать разброс данных, существует другая структурная характеристика — межквартильный размах.

Межквартильный размах — это размах половины значений набора данных, которые находятся вокруг медианы. Это ближайшие к медиане значения: меньше неё и больше.

Чтобы вычислить межквартильный размах, нужно разделить полученный набор данных на четыре части, в каждой из которых должно содержаться равное число элементов. Разберём на примере.

Имеется набор данных Сначала вычислим медиану этого набора данных. Для этого отсортируем его по возрастанию: Медиана этого набора данных равна

Как вы помните, медиана делит набор данных на две равные части: в первой половине располагаются значения, которые численно меньше медианы, во второй — значения, которые численно больше неё. Теперь для каждой из этих двух частей нужно тоже вычислить медиану. Для первых набора данных ( ) медиана равна , а для вторых — ( ) медиана равна

С помощью такого разделения мы разделили исходный набор данных на четыре равных по объёму набора данных: Красным в этом наборе обозначены вычисленные медианы. Каждая из этих границ между наборами называется квартилем:

Значение, левее которого лежит ровно всего набора данных, называют первым квартилем — Q1.
Значение, правее которого лежит ровно всего набора данных, называют третьим квартилем — Q3.
Медиану иногда называют вторым квартилем (Q2), так как между ней и первым квартилем лежит ровно всего набора данных , а также между ней и третьим квартилем лежит ровно всего набора данных.

Как найти медиану?

Медиана – это такое число в ряду, которое делит этот ряд на две одинаковые части: перед медианой находится столько же чисел, сколько и после неё.

Найти медиану ряда чисел можно следующим образом:

Отсортируйте ряд чисел по возрастанию или убыванию.
Если количество чисел в ряду нечетное, то медиана – это среднее число в отсортированном ряду.
Если число чисел в ряду четное, то медиана – это среднее арифметическое двух соседних чисел в отсортированном ряду.

Например, для ряда чисел 3, 5, 7, 2, 1, 8, 4 медианой будет число 4, так как после него находится столько же чисел, сколько и перед ним.

Ряд чисел	Отсортированный ряд	Медиана
3, 5, 7, 2, 1, 8, 4	1, 2, 3, 4, 5, 7, 8	4
1, 5, 8, 9, 17, 22	1, 5, 8, 9, 17, 22	8.5

Помните, что медиана может быть не единственной, если в ряде есть повторяющиеся числа. В этом случае медианой может быть любое из повторяющихся чисел или среднее арифметическое двух соседних повторяющихся чисел в отсортированном ряду.

Знание того, как найти медиану, может быть полезным при анализе данных и статистических измерений, а также при решении задач по математике и программированию.

Вопрос-ответ

Вопрос: Что такое среднее арифметическое?

Ответ: Среднее арифметическое — это сумма всех значений в ряду, деленная на их количество.

Вопрос: Как найти размах ряда чисел?

Ответ: Размах — это разница между наибольшим и наименьшим значением в ряду чисел. Найти его можно вычитанием наименьшего значения из наибольшего.

Вопрос: Что такое мода в ряде чисел?

Ответ: Мода — это значение, которое встречается наиболее часто в ряду чисел.

Вопрос: Что такое медиана ряда чисел?

Ответ: Медиана — это значение, которое находится посередине ряда чисел после их упорядочивания.

Вопрос: Как связаны между собой среднее арифметическое, размах, мода и медиана?

Ответ: Среднее арифметическое, размах, мода и медиана используются для описания ряда чисел и его характеристик. Например, размах показывает, насколько распределение значений в ряду разнообразно, а мода и медиана — какие значения являются наиболее типичными для данного ряда. Среднее арифметическое — это общий показатель централизации данных, позволяющий оценить их среднее значение.

Главная — Советы — Изучаем основные понятия статистики: как найти среднее арифметическое, размах, моду и медиану ряда чисел с помощью простых шагов

Статья на тему «как найти среднее арифметическое, размах, моду и медиану в ряде чисел» написана очень хорошо и понятно. Автор простым и доступным языком объясняет каждое понятие, даёт примеры и схемы, на которых иллюстрирует процесс расчёта. Очень порадовало наличие практических задач, которые помогли мне понять как применять эти понятия на практике. К сожалению, хотелось бы увидеть ещё какие-то примеры, которые помогли бы лучше запомнить и закрепить материал. В целом, статья очень полезна, и я буду её рекомендовать всем своим друзьям и знакомым.

Иван Петров
5.0 out of 5.0 stars5.0

Статья очень понравилась. Кратко и понятно объяснили, как найти среднее арифметическое, размах, моду и медиану ряда чисел. Спасибо!

Екатерина
5.0 out of 5.0 stars5.0

Статья очень наглядно и просто объясняет, как найти среднее арифметическое, размах, моду и медиану в ряде чисел. Быстро и без лишних слов. Спасибо!

Jasmine
5.0 out of 5.0 stars5.0

Статья содержит подробное описание всех понятий: среднее арифметическое, размах, мода и медиана. Наглядные примеры, простое и доступное объяснение. Очень помогла при подготовке к тесту. Но хотелось бы узнать больше про применение этих понятий в действительности.

Дмитрий
5.0 out of 5.0 stars5.0

Считаю, что статья является одной из самых полезных на тему математики и статистики, которую я когда-либо читал. Приятно удивила ясность объяснений, множество отличных примеров и обширных объяснений, которые глубоко погружаются в тему того, как найти среднее арифметическое, размах, моду и медиану ряда чисел. Нашел данную информацию на вашем ресурсе, в результате чего кардинально улучшил свои знания и умения в этой области. Но хотелось бы большей активности в вопросах создания более сложных примеров и практики на материале. В целом, статья заслуживает похвалы и изучения, буду советовать её всем своим друзьям и коллегам.

Nikita
5.0 out of 5.0 stars5.0

Хорошая статья для тех, кто не сильно разбирается в математике, но нуждается в практических знаниях. Объяснения четкие и понятные, хорошо продуманный пример помогает легко разобраться в теме. Однако, было бы круто добавить больше примеров и приложений, чтобы читатель мог закрепить свои знания более практическим способом.

Дисперсия

Самой простой способ описать разброс данных — найти среднюю сумму отклонений всех значений от полученного ранее центра. Рассмотрим на примере. Есть некоторый набор данных: Вычислим среднее арифметическое этого набора данных:

Теперь вычислим среднюю сумму отклонений каждого элемента от этого центра. Чтобы найти отклонение значения от центра, вычтем из каждой величины среднее арифметическое:

В результате получилось Такая операция приведёт нас к для любого набора данных, и доказать это можно математически. Почему так получилось и как описывать разброс, если средняя сумма отклонений всех значений равна

В этом примере отклонение каждого элемента от центра учитывалось со знаком, и в итоге все отклонения «обнулили» друг друга. Чтобы решить эту проблему, нужно избавиться от знака отклонений. Как это сделать? Взять отклонение по модулю или возвести отклонение в квадрат.

Модуль числа — это функция, которая всегда возвращает положительное число. Отрицательное число модуль меняет на противоположное: а положительное оставляет без изменений, например:

Вариант с модулем хорошо работает в теории и плохо на практике, так как вычисление модуля — не арифметическая, а логическая операция — надо проверить больше ли число, над которым производится операция. Это приводит к тому, что для него достаточно сложно определяются другие математические величины.

Возведение в квадрат — это вычислительная операция, что делает её проще для математиков, а значит, и предпочтительнее для нас. В результате мы получим величину, которая равна среднему суммы квадратов отклонений набора данных . Такая величина называется дисперсией.

Дисперсия для набора данных из элементов: вычисляется по формуле:

где — это среднее значение набора данных Знак (произносится как «сигма») означает суммирование выражений для всех значений от до . Из-за изменения значений от до , выражение принимает поочерёдно все значения выборки.

На первый взгляд формула выглядит достаточно страшно, но всё станет понятно, если разобрать её на примере.

Вернёмся к набору данных, который приводили выше: со средним значением Число элементов среднее значение а сумма выражений будет расписана так:

Подставим все значения в формулу, и тогда дисперсия будет равна:

Понятие выборки и генеральной совокупности

Слово статистика, образованное от латинского status(состояние дел), появилось только в 1746 году, когда его употребил немец Готфрид Ахенвалль. Однако ещё в Древнем Китае проводились переписи населения, в ходе которых правители собирали информацию о своих владениях и жителях, проживающих в них.

В основе любого статистического исследования лежит массив информации, который называют выборкой данных. Покажем это на примере. Пусть в классе, где учится 20 учеников, проводился тест по математике, содержавший 25 вопросов. В результате учащиеся показали следующие результаты:

Ряд чисел, приведенный во второй строке таблицы (12, 19, 19, 14, 17, 16, 18, 20, 15, 25, 13, 20, 25, 16, 17, 12, 24, 13, 21, 13), будет выборкой. Также ее могут называть рядом данных или выборочной совокупностью.

В примере с классом выборка состоит из 20 чисел. Эту величину (количество чисел в ряду) называют объемом выборки. Каждое отдельное число в ряду именуют вариантой выборки.

В примере со школьным классом в выборку попали все его ученики. Это позволяет точно определить, насколько хорошо учащиеся написали математический тест. Однако иногда необходимо проанализировать очень большие группы населения, состоящие из десятков и даже сотен миллионов человек. Например, необходимо узнать, какая часть населения страны курит. Опросить каждого жителя государства невозможно, поэтому в ходе исследования опрашивают лишь его малую часть. В этом случае статистики выделяют понятие генеральная совокупность.

Так, если с помощью опроса 10 тысяч человек ученые делают выводы о распространении курения в России, то все российское население будет составлять генеральную совокупность исследования, а опрошенные 10 тысяч людей вместе образуют выборку.

Медиана выборки

Иногда, например, при расчете средней зарплаты, среднее арифметическое не вполне адекватно отражает ситуацию. Это происходит из-за наличия в выборке чисел, очень сильно отличающихся от среднего. Так, из-за огромных зарплат некоторых начальников большинство рядовых сотрудников компаний обнаруживают, что их зарплата ниже средней. В таких случаях целесообразно использовать такую характеристику, как медиану ряда. Это такое значение, которое делит ряд данных пополам. В упорядоченном ряде 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25 медианой будет равна 12, так как именно она находится в середине ряда:

Однако таким образом можно найти только медиану ряда, в котором находится нечетное количество чисел. Если же их количество четное, то за медиану условно принимают среднее арифметическое двух средних чисел. Так, для ряда 2, 3, 6, 8, 8, 12, 15, 15, 18, 19, 25, 30, содержащего 12 чисел, медиана будет равна среднему значению 12 и 15, которые занимают 6-ое и 7-ое место в ряду:

Вернемся к примеру с математическим тестом в школе. Так как его сдавали 20 учеников, а 20 – четное число, то для расчета медианы следует найти среднее арифметическое 10-ого и 11-ого числа в упорядоченном ряде

12, 12, 13, 13, 13, 14, 15, 16, 16, 17, 17, 18, 19, 19, 20, 20, 21, 24, 25, 25.

Эти места занимают числа 17 и 17 (выделены жирным шрифтом). Медиана ряда будет равна

(17+17):2 = 34:2 = 17.

Три приведенные основные статистические характеристики выборки, а именно среднее арифметическое, мода и медиана, называются мерами центральной тенденции. Они позволяют одним числом указать значение, относительно которого группируются все числа ряда.

Рассмотрим для наглядности ещё один пример. Врач в ходе диспансеризации измерил вес мальчиков в классе. В результате он получил 10 значений (в кг):

39, 41, 67, 36, 60, 58, 46, 44, 39, 69.

Найдем среднее арифметическое, размах, моду и медиану для этого ряда.

Решение. Сначала перепишем ряд в упорядоченном виде:

36, 39, 39, 41, 44, 46, 58, 60, 67, 69.

Так как в ряде 10 чисел, то объем выборки равен 10. Найдем среднее арифметическое. Для этого сложим все числа в ряде и поделим их на объем выборки (то есть на 10):

(36+39+39+41+44+46+58+60+67+69):10 =

= 499:10 = 49,9 кг.

Размах выборки равен разнице между наибольшей и наименьшей вариантой в ней. Самый тяжелый мальчик весит 69 кг, а самый легкий – 36 кг, а потому размах ряда равен

69 – 36 = 33 кг.

В упорядоченном ряде только одно число, 39, встречается дважды, а все остальные числа встречаются по одному разу. Поэтому мода ряда будет равна 39 кг.

В выборке 10 чисел, а это четное число. Поэтому для нахождения медианы надо найти два средних по счету значение найти их среднее. На 5-ом и 6-ом месте в ряде находятся числа 44 и 46. Их среднее арифметическое равно

(44+46):2 = 90:2 = 45 кг.

Поэтому и медиана ряда будет равна 45 кг.

Почему важно знать моду числового ряда?

Одним из главных преимуществ использования моды числового ряда является возможность определить наиболее типичное значение в данном ряде чисел. Это полезно, например, при анализе данных о средних температурах, доходах или оценках учащихся. Значение моды помогает лучше понять, какова наиболее распространенная характеристика в данном контексте.

Кроме того, мода числового ряда также может быть использована для выявления аномальных значений. Если значение моды находится далеко от остальных элементов ряда, это может указывать на выбросы или необычные события, которые могут быть предметом дальнейшего анализа.

Знание моды числового ряда также может быть полезным при принятии решений. Например, при планировании производства товаров или определении наиболее востребованных продуктов или услуг. Предварительный анализ ряда числовых данных, включая моду, может помочь сделать более обоснованные и эффективные решения.

В целом, знание моды числового ряда является важным инструментом в алгебре и статистике, позволяющим проводить более точный анализ данных, выявлять аномальные значения и принимать обоснованные решения на основе имеющихся числовых данных.

Стандартное отклонение

Если присмотреться к формуле дисперсии, может возникнуть вопрос: «Почему дисперсия обозначается величиной Кто такая эта ».

Дело в том, что дисперсия обладает одним серьёзным недостатком: если набор значений исчисляется в некоторых единицах измерения (например, рублях), то дисперсия будет равна квадрату этих единиц измерения (рубли^). Но объяснить, что это такое рубли, достаточно сложно. Тем более иметь разброс в той же единице измерения, в которой измеряется исходная величина, достаточно удобно и логично. Поэтому используется ещё одна дополнительная величина, описывающая разброс, — стандартное отклонение.