Формулы приведения, их доказательство, примеры

История и происхождение числа Пи

Пи – это математическая константа, представляющая отношение длины окружности к ее диаметру. Это одно из самых важных и известных математических понятий, и его значение изучалось на протяжении тысячелетий. Символом числа пи является греческая буква ?, и это иррациональное число, которое продолжается бесконечно, не повторяясь.

Самое раннее известное вычисление числа пи было сделано древним вавилонским математиком около 2000 г. до н.э. Они обнаружили, что число пи равно 3,125.
Первое точное приближение числа пи было сделано греческим математиком Архимедом в 3 веке до нашей эры. Он использовал метод, называемый «описанием и вписыванием», когда он рисовал многоугольники вокруг и внутри круга, чтобы оценить его окружность и диаметр.
Символ ? впервые был использован для обозначения этого отношения валлийским математиком Уильямом Джонсом в 1706 г., а позже он был популяризирован швейцарским математиком Леонардом Эйлером в 18 веке.

На протяжении веков многие математики внесли свой вклад в изучение числа пи, в том числе китайские, индийские и персидские. ученые. Первая десятичная аппроксимация числа пи была вычислена английским математиком Уильямом Броункером в 1655 году, а затем уточнена многими другими.

Сегодня число пи является фундаментальной константой в математике и естественных науках и встречается в бесчисленных уравнения и формулы. Его значение было вычислено с помощью компьютеров до триллионов знаков после запятой, и оно продолжает очаровывать и бросать вызов математикам по всему миру.

Год	Значение числа Пи	Метод расчета
2000 г. до н.э.	3,125	Неизвестно
3 век до н.э.	3.1418	Метод Архимеда
1655	3.1415927	Метод Броункера
2021	3.141592653589793238	Компьютерный расчет

Несмотря на долгую историю числа пи, об этом загадочном и увлекательном числе еще многое предстоит узнать. От своего древнего происхождения до современных расчетов число Пи продолжает вызывать любопытство и удивление у людей всех возрастов и слоев общества.

Роль пи минус альфа в технических и инженерных областях

Понятие пи минус альфа имеет важное значение в различных технических и инженерных областях. Пи минус альфа представляет собой разность между числовым значением пи и углом альфа

В аэродинамике пи минус альфа используется для расчета и анализа динамического поведения летательного аппарата. Это понятие играет особую роль при определении аэродинамических характеристик, таких как аэродинамическое подъемное сопротивление и момент вокруг продольной оси. Значение пи минус альфа позволяет инженерам прогнозировать и оптимизировать работу летательных аппаратов в различных условиях полета.

Во многих областях инженерии, таких как механика, электротехника и тепловые науки, пи минус альфа используется для моделирования и анализа систем. Знание данной величины позволяет инженерам предсказывать и управлять поведением системы в различных условиях. Например, в механике пи минус альфа может быть использовано для определения траектории движения объекта или расчета сил, действующих на него.

Также в области сигнальной обработки и телекоммуникаций пи минус альфа играет важную роль. Оно может использоваться для компенсации и коррекции искажений сигналов при передаче данных. Знание значения пи минус альфа позволяет инженерам проводить точную обработку сигналов и повышать качество передачи информации.

Итак, пи минус альфа имеет большое значение в различных технических и инженерных областях, где оно используется для моделирования, анализа и оптимизации систем. Понимание этого понятия позволяет инженерам разрабатывать и улучшать технологии, повышать эффективность работы систем и обеспечивать высокое качество продукции и услуг.

Другие математические открытия

Древние цивилизации также сделали другие математические открытия, основанные на их понимании числа пи. Египтяне, например, использовали приближение пи для вычисления площади круга и объема цилиндра. Они также использовали теорему Пифагора и золотое сечение в своих построениях.

Вавилоняне имели глубокое понимание геометрии и могли вычислять площади треугольников, прямоугольников и трапеций, используя основные алгебраические методы. Они также разработали концепцию нуля и имели элементарные знания об алгебраических уравнениях.

Цивилизация	Приближение числа Пи	Математика Открытия
Египтяне	4/3	Теорема Пифагора, золотое сечение, площадь & объем цилиндра
Вавилоняне	3 1/8 или 3,125	Геометрия, ноль, алгебраические уравнения, лунный календарь
Китайский	355/113	Алгебра, десятичные дроби, тригонометрия

Возможно, у древних цивилизаций не было такой строгой математической основы, как у современных стран, но их вклад в математику и науку неизмерим. Они заложили основу для современных открытий и будут продолжать вдохновлять будущие поколения.

Формулы приведения. Как запомнить?

Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.

Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.

Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:

задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.

И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.

Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?

Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов

Формулы приведения:

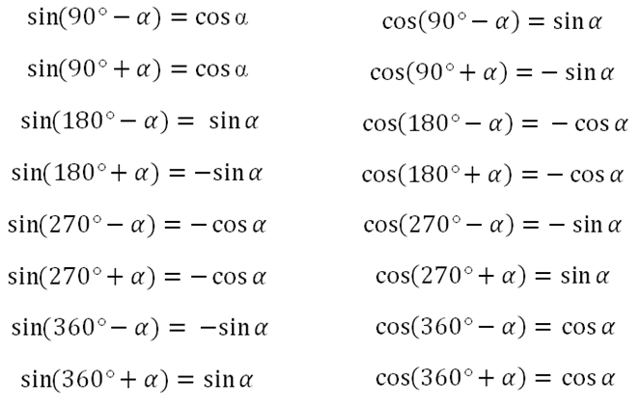
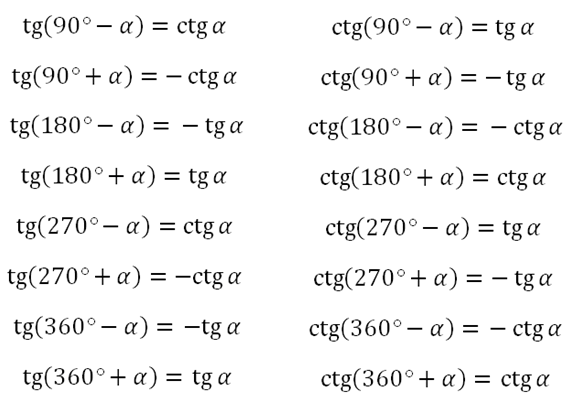
Угол альфа лежит пределах от 0 до 90 градусов.

Итак, необходимо уяснить «закон», который здесь работает:

Определите знак функции в соответствующей четверти.

Напомню их:

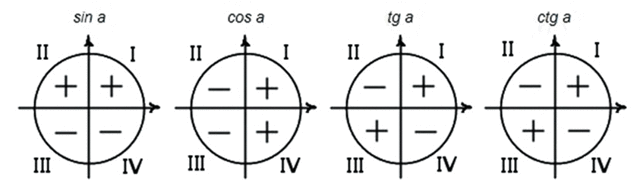
Запомните следующее:

Функция изменяется на кофункцию

Функция на кофункцию не изменяется

Что означает понятие — функция изменяется на кофункцию?

Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.

Теперь по представленному закону запишем несколько формул приведения самостоятельно:

Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:

Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов.
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов.
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов.

Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.

В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.

И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения.

Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.

В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!

Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.

Символы вероятности и статистики

Символ	Название символа	Значение / определение	пример
P ( А )	функция вероятности	вероятность события A	P ( A ) = 0,5
P ( A ⋂ B )	вероятность пересечения событий	вероятность того, что событий A и B	P ( A ⋂ B ) = 0,5
P ( A ⋃ B )	вероятность объединения событий	вероятность того, что событий A или B	P ( A ⋃ B ) = 0,5
P ( A \| B )	функция условной вероятности	вероятность события A данное событие B произошло	P ( A \| B ) = 0,3
f ( x )	функция плотности вероятности (pdf)	P ( a ≤ x ≤ b ) = ∫ f ( x ) dx
F ( х )	кумулятивная функция распределения (cdf)	F ( х ) = Р ( Х ≤ х )
μ	Средняя численность населения	среднее значение совокупности	μ = 10
E ( X )	ожидаемое значение	ожидаемое значение случайной величины X	E ( X ) = 10
E ( X \| Y )	условное ожидание	ожидаемое значение случайной величины X с учетом Y	E ( X \| Y = 2 ) = 5
var ( X )	отклонение	дисперсия случайной величины X	var ( X ) = 4
σ 2	отклонение	дисперсия значений совокупности	σ 2 = 4
std ( X )	стандартное отклонение	стандартное отклонение случайной величины X	std ( X ) = 2
σ _X	стандартное отклонение	значение стандартного отклонения случайной величины X	σ _X = 2
	медиана	среднее значение случайной величины x
cov ( X , Y )	ковариация	ковариация случайных величин X и Y	cov ( X, Y ) = 4
корр ( X , Y )	корреляция	корреляция случайных величин X и Y	корр ( X, Y ) = 0,6
ρ _{X , Y}	корреляция	корреляция случайных величин X и Y	ρ _{X , Y} = 0,6
∑	суммирование	суммирование — сумма всех значений в диапазоне ряда
∑∑	двойное суммирование	двойное суммирование
Пн	Режим	значение, которое чаще всего встречается в популяции
MR	средний диапазон	MR = ( x _макс + x _мин ) / 2
Мкр	медиана выборки	половина населения ниже этого значения
Q ₁	нижний / первый квартиль	25% населения ниже этого значения
₂ квартал	медиана / второй квартиль	50% населения ниже этого значения = медиана выборки
₃ квартал	верхний / третий квартиль	75% населения ниже этого значения
х	выборочное среднее	среднее / среднее арифметическое	х = (2 + 5 + 9) / 3 = 5,333
с 2	выборочная дисперсия	оценщик дисперсии выборки населения	s 2 = 4
с	стандартное отклонение выборки	Оценка стандартного отклонения выборки населения	s = 2
z _x	стандартная оценка	z _x = ( x — x ) / s _x
X ~	распределение X	распределение случайной величины X	X ~ N (0,3)
N ( μ , σ 2 )	нормальное распределение	гауссово распределение	X ~ N (0,3)
U ( а , б )	равномерное распределение	равная вероятность в диапазоне a, b	Х ~ U (0,3)
ехр (λ)	экспоненциальное распределение	f ( x ) = λe — λx , x ≥0
гамма ( c , λ)	гамма-распределение	f ( x ) = λ cx c-1 e — λx / Γ ( c ), x ≥0
χ 2 ( к )	распределение хи-квадрат	f ( x ) = x k / 2-1 e — x / 2 / (2 k / 2 Γ ( k / 2))
F ( k ₁ , k ₂ )	F распределение
Корзина ( n , p )	биномиальное распределение	f ( k ) = _n C _k p k (1 -p ) nk
Пуассон (λ)	распределение Пуассона	е ( К ) знак равно λ К е — λ / К !
Геом ( p )	геометрическое распределение	f ( k ) = p (1 -p ) k
HG ( N , K , n )	гипергеометрическое распределение
Берн ( p )	Распределение Бернулли

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает: или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:, Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса ~~болтается как~~ как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси на влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения: – все действительные числа, кроме … , , , … и т. д. или коротко: , где – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси к значению справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси к значению слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Определение знака

Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.

Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.

Дополнительные сведения

Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно).

Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180

Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).

Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).

Построение окружности

Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».

Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:

Координаты заключаются в круглые скобки и разделяются «;».
На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).

Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:

Значения по x и y больше 0 соответствуют первой четверти (I).
II: x<0 и y>0.
III: x<0 и y<0.
IV: x>0 и y<0.

Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям. Рекомендуется отметить для удобства значения углов в радианах рядом с точками пересечения следующим образом:

0 и 2ПИ (0 и 360 градусов) — (1;0).
ПИ/2 (90) — (0;1).
3ПИ/2 (270) — (1;0).

Использование готового инструмента

Однако необязательно самостоятельно чертить единичную окружность для определения знаков. Можно воспользоваться уже готовыми вариантами (например, рис. 1).

Рисунок 1. Пример тригонометрического круга.

Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:

cos(-a) = cos(a).
sin(-a) = -sin(a).
tg(-a) = -tg(a).
ctg(-a) = -ctg(a).

С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:

Определить четверть, в которой находится угол: 240 = 4ПИ/3 соответствует III четверти.
В III четверти величина функции принимает только отрицательные значения. Значит, перед ней следует поставить знак «минус».
Вычислить: cos(4ПИ/3) = — 1/2.

Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.

Часто используемые знаки и символы математики

Δ Σ Ψ Ω α β γ δ ε η θ λ μ ν ξ π ρ σ τ υ φ χ ψ ω

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

a b c d e f g h i j k l m n o p q r s t u v w x y z

основные символы

×знак умножения

⋅умножение ‘точка’

⊗ векторное произведение

⊕ векторная сумма

÷знак деления

⊥ортогонально, перпендикулярно

≤меньше или равно

≥больше или равно

≈приблизительно равно (асимптотически равно)

≠не равно

±плюс-минус

∞знак бесконечность

∑знак суммирования

∂частичный дифференциал

∫интеграл

≅approximately equal to

Греческие заглавныеГреческие строчные Математическиезнаки и символы

Α альфа

Β бета

Γ гамма

Δ дельта

Ε эпсилон

Ζ дзета

Η эта

Θ тета

Ι иота

Κ каппа

Λ лямбда

Μ мю

Ν ню

Ξ кси

Ο омикрон

Π пи

Ρ ро

Σ сигма

Τ тау

Υ ипсилон

Φ фи

Χ хи

Ψ пси

Ω омега

α альфа

β бета

γ гамма

δ дельта

ε эпсилон

ζ дзета

η эта

θ тета

ι иота

κ каппа

λ лямбда

μ мю

ν ню

ξ кси

ο омикрон

π пи

ρ ро

ς сигма (final)

σ сигма

τ тау

υ ипсилон

φ фи

χ хи

ψ пси

ω омега

×знак умножения

÷знак деления

≤меньше или равно

≥больше или равно

≈приблизительно равно (асимптотически равно)

≠не равно

≡тождественно, совпадает с

±плюс-минус

¼одна четвёртая

½одна вторая

¾три четверти

√квадратный корень (радикал)

∞знак бесконечность

∑знак суммирования

∏произведение последовательности — знак произведения

∂частичный дифференциал

∫интеграл

∀для всех

∃существует

∅пустое множество; диаметр **

∇набла

∉ не принадлежит **

∋ содержит

∗оператор ‘звездочка’ **

∝пропорционально

∠угол

∧логическое И — wedge

∨логическое ИЛИ — vee

∩пересечение — cap

∪объединение — cup

∴следовательно

∼знак тильда — ‘изменяется с’ — знак подобия

≅approximately equal to **

⊂является подмножеством

⊃является надмножеством

⊄не является подмножеством **

⊆является подмножеством либо равно

⊇является надмножеством либо равно

⊕плюс в кружке

⊗знак умножения в кружке

⊥ортогонально, перпендикулярно

⋅оператор ‘точка’ **

ƒзнак функции

Рекорды в вычислении числа пи

Число пи — единственная математическая константа, которая столь часто привлекает внимание обычных людей. Во многом это связано с тем, что вычисление пи относится к кругу проблем, которые не могут быть полностью решены

За последние несколько десятилетий были установлены многие рекорды в вычислении пи.

В 2019 году британский инженер Эмма Харукава установила новый мировой рекорд — она вычислила число пи до 31,4 триллиона знаков после запятой. Расчет занял 121 день, и был выполнен на кластере компьютеров в Японии. Предыдущий рекорд был установлен в 2016 году, когда Питер Труфильо довел точность вычисления до 22,4 триллионов знаков.

Другой способ установить рекорд пи состоит в том, чтобы вычислить максимальное количество знаков за определенное время. Такой рекорд установил Джон Макнерни, который смог вычислить более 500 миллионов знаков за 29 часов. Он использовал кластер из 50 компьютеров, которые работали одновременно.

Вычисление пи — это не только результативно, но и довольно занимательно. Вычисление пи содержит множество способов и методов, некоторые из которых имеют древние корни. Предыдущие рекорды показывают, что возможности улучшить результат находятся далеко не на пределах современной вычислительной техники.

Применение минус пи на окружности

Минус пи на окружности, обозначаемое символом π, представляет собой точку на окружности, которая находится на расстоянии π от начальной точки окружности, измеряемого в радианах. Это важная точка, которая широко применяется в математике и физике.

Применение минус пи на окружности:

Геометрия: минус пи на окружности помогает определить положение точки на окружности относительно начальной точки. Если точка находится на минус пи, она располагается на противоположном конце окружности от начальной точки.
Тригонометрия: минус пи на окружности является своеобразным «началом» тригонометрических функций, таких как синус и косинус. Синус и косинус минус пи равны нулю, что позволяет использовать это значение для упрощения расчетов и построений графиков.
Физика: минус пи на окружности используется для определения фаз и сдвигов волны. Для синусоидальных колебаний, минус пи представляет момент, когда колебание достигает своего максимального отрицательного значения.

Использование минус пи на окружности позволяет упростить расчеты и разработку моделей в различных областях, где присутствуют окружности и тригонометрия.

Формулы приведения. Быстро и легко!

Тригонометрия.Формулы приведения.

Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода.

Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.

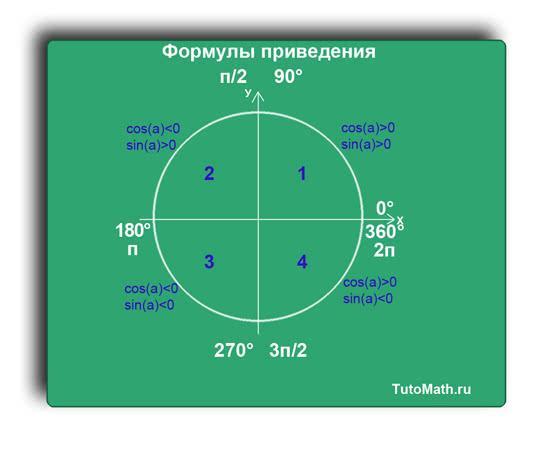
Разберем в каждой четверти функции sin(a) и cos(a). Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.

В первой четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти. И функция cos(a)>0, потому что ось X положительна в этой четверти.

Первую четверть можно описать через градусную меру, как (90-α) или (360+α).

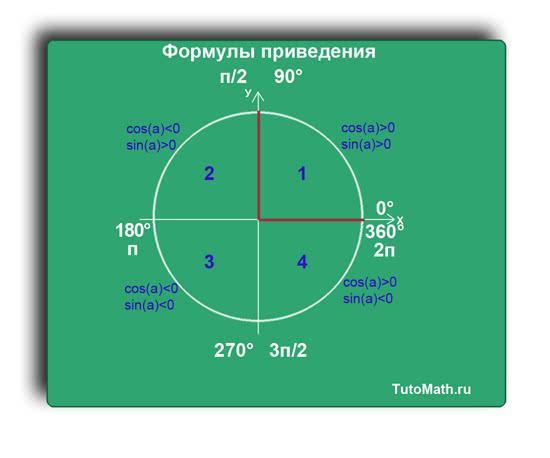
Во второй четверти видно, что функция sin(a)>0, потому что ось Y положительна в этой четверти.
А функция cos(a)

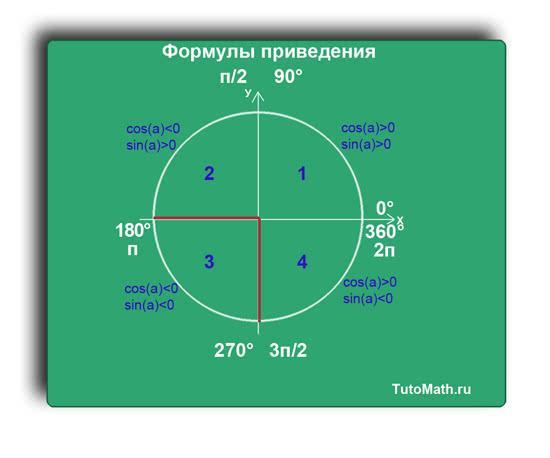
В четвертой четверти видно, что функция sin(a)0, потому что ось X положительна в этой четверти.Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).

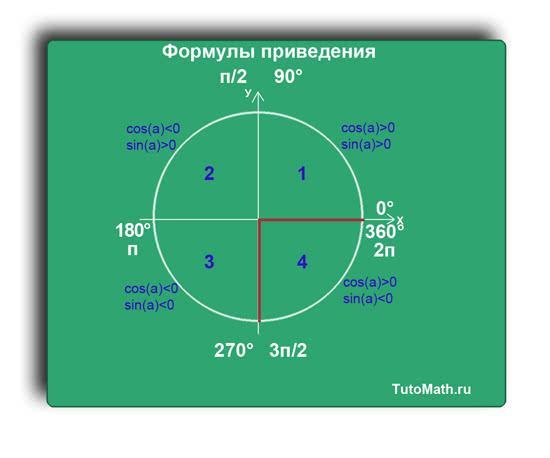
Теперь рассмотрим сами формулы приведения.

Запомним простой алгоритм:

Четверть. (Всегда смотрите в какой вы четверти находитесь).
Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется.

И так начнем разбирать по четвертям данный алгоритм.

Выясни чему будет равно выражение cos(90-α)

Рассуждаем по алгоритму:

Четверть первая.
В первой четверти знак у функции косинуса положительный.
В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.

Будет cos(90-α) = sin(α).

Формулы отрицательных углов

Что такое отрицательный угол и как с ним работать? На самом деле, все просто: чтобы получить отрицательный угол, достаточно поставить перед аргументом минус. Например, sin(-x).

Применять такой угол при решении выражений с тригонометрическими функциями очень неудобно, поэтому от минуса обычно избавляются. Однако делать это нужно по правилам: нельзя просто его не написать.

Чтобы правильно избавиться от минуса, нужно понимать, что отрицательные углы напрямую связаны с графиками тригонометрических функций, а именно с четностью функций. Подробнее про четность функции можно прочесть в статье «Определение и график функции».

Четность функции можно сравнить со снежинкой. Если мы посмотрим на нее под микроскопом и мысленно проведем ось посередине, то окажется, что левая и правая части одинаковые. Единственное их отличие – они отзеркалены.

Также и четные функции: справа и слева они имеют одинаковые отзеркаленные части.

Четная функция – функция, для которой выполняется равенство \(f(x)=f(-x)\).

Повторим, такие функции симметричны относительно оси ординат. Можно представить, что вместо оси у у нас стоит зеркало, в которой график функции отражается.

Если мы вспомним графики тригонометрических функций и проверим их симметричность, то заметим, что четным является только косинус. Этим он выделяется среди других функций.

Синус, тангенс и котангенс – нечетные функции. Для них будет справедливо уравнение \(f(-x)=-f(x)\). Их графики не симметричны относительно оси у.

Таким образом, опираясь на четность функции, мы можем вывести четыре формулы:

\(cos(-x)=cos x\)\(sin(-x)=-sin x\)\(tg(-x)=-tg x\)\(ctg(-x)=-ctg x\)

Пользуясь этими формулами, можно легко избавляться от минуса в аргументах функции.

Итак, мы попробовали изменить аргумент с помощью минуса. А если попробовать поставить перед аргументом коэффициент, например, 2?

График квадратичной, кубической функции, график многочлена

Парабола. График квадратичной функции () представляет собой параболу. Рассмотрим знаменитый случай:

Вспоминаем некоторые свойства функции .

Область определения – любое действительное число (любое значение «икс»). Что это значит? Какую бы точку на оси мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так: . Область определения любой функции стандартно обозначается через или . Буква обозначает множество действительных чисел или, проще говоря, «любое икс» (когда работа оформляется в тетради, пишут не фигурную букву , а жирную букву R).

Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае: – множество всех положительных значений, включая ноль. Область значений стандартно обозначается через или .

Функция является чётной. Если функция является чётной, то ее график симметричен относительно оси . Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции выражается условием . Как проверить любую функцию на чётность? Нужно вместо подставить в уравнение . В случае с параболой проверка выглядит так: , значит, функция является четной.

Функция не ограничена сверху. Аналитически свойство записывается так: . Вот вам, кстати, и пример геометрического смысла предела функции: если мы будем уходить по оси (влево или вправо) на бесконечность, то ветки параболы (значения «игрек») будут неограниченно уходить вверх на «плюс бесконечность».

При изучении пределов функций желательно понимать геометрический смысл предела.

Я не случайно так подробно расписал свойства функции, все вышеперечисленные вещи полезно знать и помнить при построении графиков функций, а также при исследовании графиков функций.

Пример 2

Построить график функции .

В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. Я предлагаю следующий алгоритм построения.

Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю:

Если с производными плохо, следует ознакомиться с уроком Как найти производную?

Итак, решение нашего уравнения: – именно в этой точке и находится вершина параболы. Почему это так, можно узнать из теоретической статьи о производной и урока об экстремумах функции. А пока рассчитываем соответствующее значение «игрек»:

Таким образом, вершина находится в точке

Теперь находим другие точки, при этом нагло пользуемся симметричностью параболы. Следует заметить, что функция – не является чётной, но, тем не менее, симметричность параболы никто не отменял.

В каком порядке находить остальные точки, думаю, будет понятно из итоговой таблицы:

Данный алгоритм построения образно можно назвать «челноком» или принципом «туда-сюда» ~~с Анфисой Чеховой~~.

Выполним чертеж:

Из рассмотренных графиков вспоминается еще один полезный признак:

Для квадратичной функции () справедливо следующее:

Если , то ветви параболы направлены вверх.

Если , то ветви параболы направлены вниз.

Углублённые знания о кривой можно получить на уроке Гипербола и парабола.

Использование

В греческом языке альфа передаёт звук .

Прописная буква альфа не используется как символ, потому что она пишется так же, как и заглавная латинская буква A.

Строчная буква α используется как символ для обозначения:

Плоских углов (вместе с другими греческими буквами);
Углового ускорения и коэффициента теплоотдачи в физике;
Альфа-частицы, альфа-излучения и альфа-распада в физике, а также для обозначения постоянной тонкой структуры;
Коэффициента поглощения в физике;
Альфа-ритма, одного из ритмов, регистрируемых с помощью электроэнцефалограммы.
В астрономии:
- Ярчайшей звезды созвездия (например, Альфа Центавра);
- Прямого восхождения, RA — одной из небесных координат;
В лямбда-исчислении — α-конверсия;
Коволюм пороховых газов во внутренней баллистике;
Бесконечно малая функция/последовательность в математическом анализе.

Свойства тригонометрических функций[]

Функция y = cos x — чётная. Функции: y = sin x, y = tg x, y = ctg x — нечётные, то есть:

sin⁡(−x)=−sin⁡x,{\displaystyle \sin \left( — x \right) = — \sin x\,,}

cos⁡(−x)=cos⁡x,{\displaystyle \cos \left( — x \right) = \cos x\,,}

tg(−x)=−tgx,{\displaystyle \mathop{\mathrm{tg}}\, \left( — x \right) = — \mathop{\mathrm{tg}}\, x\,,}

ctg(−x)=−ctgx.{\displaystyle \mathop{\mathrm{ctg}}\, \left( — x \right) = — \mathop{\mathrm{ctg}}\, x\,.}

Для острых углов α<π2{\displaystyle \alpha < \frac{ \pi}{2}\,\!}
справедливо:

sin⁡(π2−α)=cos⁡α,{\displaystyle \sin \left( \frac{ \pi}{2} — \alpha \right) = \cos \alpha\,,}

cos⁡(π2−α)=sin⁡α,{\displaystyle \cos \left( \frac{ \pi}{2} — \alpha \right) = \sin \alpha\,,}

tg(π2−α)=ctgα,{\displaystyle \mathop{\mathrm{tg}}\, \left( \frac{ \pi}{2} — \alpha \right) = \mathop{\mathrm{ctg}}\, \alpha\,,}

ctg(π2−α)=tgα.{\displaystyle \mathop{\mathrm{ctg}}\, \left( \frac{ \pi}{2} — \alpha \right) = \mathop{\mathrm{tg}}\, \alpha\,.}

Для углов <α<π{\displaystyle 0 < \alpha < \pi \,\!} справедливо:

sin⁡(π−α)=sin⁡α,{\displaystyle \sin \left( \pi — \alpha \right) = \sin \alpha\,,}

cos⁡(π−α)=−cos⁡α,{\displaystyle \cos \left( \pi — \alpha \right) = — \cos \alpha\,,}

tg(π−α)=−tgα,α≠π2.{\displaystyle \mathop{\mathrm{tg}}\, \left( \pi — \alpha \right) = — \mathop{\mathrm{tg}}\, \alpha, \qquad \alpha \ne \frac{ \pi}{2}\,.}

Рассмотрим треугольник ABO (см. Рис. 1). По теореме Пифагора:

(AB)2+(BO)2=(OA)2,{\displaystyle \left(AB \right)^2 + \left(BO \right)^2 = \left(OA \right)^2 \,,}

если OA = 1, то AB = sin α и OB = cos α, то есть

sin2⁡α+cos2⁡α=1.(1){\displaystyle \sin^2 \alpha + \cos^2 \alpha = 1. \qquad \qquad (1)\,}

Если разделить выражение (1) на cos2⁡α,{\displaystyle \cos^2 \alpha \,,} то получим следующее тождество:

1+tg2α=1cos2⁡α.(2){\displaystyle 1 + \mathop{\mathrm{tg}}\,^2 \alpha = \frac{1}{ \cos^2 \alpha}. \qquad \qquad (2) \,}

Если разделить выражение (1) на sin2⁡α,{\displaystyle \sin^2 \alpha \,,} то получим следующее тождество:

1+1tg2α=1sin2⁡α,(3){\displaystyle 1 + \frac{1}{ \mathop{\mathrm{tg}}\,^2 \alpha} = \frac{1}{ \sin^2 \alpha}, \qquad \qquad (3) \,}

или

1+ctg2α=1sin2⁡α.(4){\displaystyle 1 + \mathop{\mathrm{ctg}}\,^2 \alpha = \frac{1}{ \sin^2 \alpha}. \qquad \qquad (4) \,}