Описание изменения величин при помощи целых чисел
Пришло время поговорить о том, для чего вообще нужны целые числа.
Основное предназначение целых чисел заключается в том, что с их помощью удобно описывать изменение количества каких-либо предметов. Разберемся с этим на примерах.
Пусть на складе находится некоторое количество деталей. Если на склад привезут еще, к примеру, 400 деталей, то количество деталей на складе увеличится, а число 400 выражает это изменение количества в положительную сторону (в сторону увеличения). Если же со склада заберут, например, 100 деталей, то количество деталей на складе уменьшится, а число 100 будет выражать изменение количества в отрицательную сторону (в сторону уменьшения). На склад не будут привозить детали, и не будут увозить детали со склада, то можно говорить о неизменности количестве деталей (то есть можно будет говорить о нулевом изменении количества).
В приведенных примерах изменение количества деталей можно описать при помощи целых чисел 400 , −100 и 0 соответственно. Положительное целое число 400 показывает изменение количества в положительную сторону (увеличение). Отрицательное целое число −100 выражает изменение количества в отрицательную сторону (уменьшение). Целое число 0 показывает, что количество осталось без изменения.
Удобство использования целых чисел по сравнению с использованием натуральных чисел заключается в том, что не нужно явно указывать увеличивается количество или уменьшается, — целое число определяет изменение количественно, а знак целого числа указывает направление изменения.
Целые числа также могут выражать не только изменение количества, но и изменение какой-либо величины. Разберемся с этим на примере изменения температуры.
Повышение температуры, скажем, на 4 градуса выражается положительным целым числом 4 . Понижение температуры, например, на 12 градусов можно описать отрицательным целым числом −12 . А неизменность температуры – это ее изменение, определяемое целым числом 0 .
Отдельно нужно сказать о трактовке отрицательных целых чисел как величины долга. Например, если у нас есть 3 яблока, то целое положительное число 3 показывает количество яблок, которыми мы владеем. С другой стороны, если мы должны кому-либо отдать 5 яблок, а у нас их нет в наличии, то эту ситуацию можно описать при помощи отрицательного целого числа −5 . В этом случае мы «обладаем» −5 яблоками, знак минус указывает на долг, а число 5 определяет долг количественно.
Понимание отрицательного целого числа в качестве долга позволяет, например, обосновать правило сложения отрицательных целых чисел. Приведем пример. Если кто-то должен 2 яблока одному человеку и одно яблоко – другому, то общий долг составляет 2+1=3 яблока, поэтому −2+(−1)=−3 .
Источник
Описание[править]
Для того чтобы все результаты вычислений в программе могли быть представлены целочисленными переменными (манипулирование данными целого типа повышает быстродействие программы и является естественным для приложений компьютерной графики), вычисления и сравнения площадей треугольников заменяются вычислениями и сравнениями их удвоенных площадей. Тем самым исключается погрешность округления при программной реализации всего алгоритма, в целом.
Аргументами функции, реализующей проверку принадлежности данной точки данному многоугольнику произвольного вида, являются
указатель на массив пар целочисленных координат вершин многоугольника, а именно, на массив структур вида
struct Point {
int x;
int y;
};
- число вершин многоугольника;
- целочисленное значение координаты X заданной точки;
- целочисленное значение координаты Y заданной точки.
Функция возвращает 1, если точка принадлежит многоугольнику, иначе — 0.
Функция имеет следующий вид.
int IsPointInsidePolygon (Point *p, int Number, int x, int y)
{
int i1, i2, n, N, S, S1, S2, S3, flag;
N = Number;
for (n=0; n<N; n++)
{
flag = 0;
i1 = n < N-1 ? n + 1 : 0;
while (flag == 0)
{
i2 = i1 + 1;
if (i2 >= N)
i2 = 0;
if (i2 == (n < N-1 ? n + 1 : 0))
break;
S = abs (p.x * (p.y - p.y) +
p.x * (p.y - p.y) +
p.x * (p.y - p.y));
S1 = abs (p.x * (p.y - y) +
p.x * (y - p.y) +
x * (p.y - p.y));
S2 = abs (p.x * (p.y - y) +
p.x * (y - p.y) +
x * (p.y - p.y));
S3 = abs (p.x * (p.y - y) +
p.x * (y - p.y) +
x * (p.y - p.y));
if (S == S1 + S2 + S3)
{
flag = 1;
break;
}
i1 = i1 + 1;
if (i1 >= N)
i1 = 0;
break;
}
if (flag == 0)
break;
}
return flag;
}
Декартова система координат.
Фиксируем в пространстве точку \(O\) и рассмотрим произвольную точку \(M\). Радиус-вектором точки \(M\) по отношению к точке \(O\) называется вектор \(\overrightarrow{OM}\). Если в пространстве кроме точки \(O\) выбран некоторый , то точке \(M\) сопоставляется упорядоченная тройка чисел — компоненты ее радиус-вектора.
Определение.
Декартовой системой координат в пространстве называется совокупность точки и базиса.
Точка носит название начала координат. Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат; первая — осью абсцисс, вторая — осью ординат, третья — осью аппликат. Плоскости, проходящие через оси координат, называются координатными плоскостями.
Определение.
Пусть дана декартова система координат \(O\), \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\). Компоненты \(x\), \(y\), \(z\) радиус-вектора \(\overrightarrow{OM}\) точки \(M\) называются координатами точки \(M\) в данной системе координат:
$$
\overrightarrow{OM} = x\boldsymbol{e_{1}} + y\boldsymbol{e_{2}} + z\boldsymbol{e_{3}}.\nonumber
$$
Первая координата называется абсциссой, вторая — ординатой, а третья — аппликатой.
Аналогично определяются координаты на плоскости и на прямой линии. Разумеется, точка на плоскости имеет только две координаты, а на прямой линии — одну.
Координаты точки пишут в скобках после буквы, обозначающей точку. Например, запись \(A(2,\ 1/2)\) означает, что точка \(A\) имеет координаты 2 и 1/2 в ранее выбранной декартовой системе координат на плоскости (рис. 2.1).
Рис. 2.1
Координаты точки, как и компоненты вектора, — величины безразмерные. В частности, они не зависят от выбранной единицы измерения длин. В самом деле, раскладывая векторы в теореме о , мы сводили дело к разложению вектора по коллинеарному с ним ненулевому вектору. А в этом случае компонента равна .
Легко видеть, что при заданной системе координат координаты точки определены однозначно. С другой стороны, если задана система координат, то для каждой упорядоченной тройки чисел найдется единственная точка, имеющая эти числа в качестве координат. Система координат на плоскости определяет такое же соответствие между точками плоскости и парами чисел. Задание системы координат на прямой линии сопоставляет каждой точке вещественное число и каждому числу — точку.
Рис. 2.2
Рассмотрим две точки \(A\) и \(B\), координаты которых относительно некоторой декартовой системы координат \(O\), \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\) соответственно \(x_{1}\), \(y_{1}\), \(z_{1}\) и \(x_{2}\), \(y_{2}\), \(z_{2}\). Поставим себе задачу найти компоненты вектора \(\overrightarrow{AB}\). Очевидно, что \(\overrightarrow{AB} = \overrightarrow{OB}-\overrightarrow{OA}\) (рис. 2.2). Компоненты радиус-векторов \(\overrightarrow{OA}\) и \(\overrightarrow{OB}\) равны (\(x_{1}\), \(y_{1}\), \(z_{1}\)) и (\(x_{2}\), \(y_{2}\), \(z_{2}\)) по определению координат. Из ранее доказанного следует, что \(\overrightarrow{AB}\) имеет компоненты (\(x_{2}-x_{1}\), \(y_{2}-y_{1}\), \(z_{2}-z_{1}\)). Этим доказано следующее утверждение.
Утверждение 1.
Чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала.
Телесный угол
Телесный угол, стянутый поверхностью SSS, относительно начала координат равен по величине площади сферы с единичным радиусом, покрытой проекцией поверхности SSS на эту сферу. В общем случае телесный угол вычисляется как
Ω=∬Sn⃗⋅dSr2,\Omega = \iint\limits_S \frac{\vec{n} \cdot dS}{r^2},Ω=S∬r2n⋅dS,
где dSdSdS — площадь бесконечно малой площадки поверхности, n⃗\vec{n}n — нормаль к площадке поверхности, rrr — расстояние от начала координат до центра площадки.
Телесный угол, стянутый треугольником, относительно начала координат вычисляется как
Ω=2atana⃗⋅(b⃗×c⃗)∣a⃗∣∣b⃗∣∣c⃗∣+∣a⃗∣(b⃗⋅c⃗)+∣b⃗∣(a⃗⋅c⃗)+∣c⃗∣(a⃗⋅b⃗).\Omega = 2 \, \text{atan} \frac{\vec{a}\cdot(\vec{b}\times\vec{c})} {|\vec{a}||\vec{b}||\vec{c}| + |\vec{a}|(\vec{b}\cdot\vec{c}) + |\vec{b}|(\vec{a}\cdot\vec{c}) + |\vec{c}|(\vec{a}\cdot\vec{b})}.Ω=2atan∣a∣∣b∣∣c∣+∣a∣(b⋅c)+∣b∣(a⋅c)+∣c∣(a⋅b)a⋅(b×c).
Используя эту формулу, телесный угол трехмерного многогранника вычисляется как сумма телесных углов всех его граней. Сумма будет равна 4π4\pi4π, если начало координат находится внутри многогранника, 2π2\pi2π, если начало координат находится на одной из граней и нулю, если начало координат находится снаружи многогранника.
Эта формула работает для любых замкнутых многогранников и является обобщением понятия порядка точки относительно кривой на трехмерный случай. Формула используется для определения положения точки относительно многогранника, что полезно для определения факта пересечения двух многогранников.
Теперь у нас есть все необходимое, чтобы вычислить объем затопленного отсека. Однако, наш отсек пересекается плоскостью поверхности воды, и нам нужно вычислить только объем отсека, находящийся под этой плоскостью. Чтобы это сделать, нам надо разбить эту плоскость на треугольники. Тогда эта плоскость заменит верхнюю часть отсека. Конечно, если мы предположим, что многоугольник выпуклый, то мы можем замкнуть все трегольники на центре этого многоугольника, но в общем случае многоугольник может быть невыпуклым, а это означает, что надо использовать полноценный метод триангуляции.
Применение координатных чисел
Координатные числа — это система числовых значений, которая используется для определения позиции точки на плоскости или в пространстве. Применение координатных чисел широко распространено в различных областях, включая математику, физику, географию, инженерию и многое другое.
Математика:
В математике координатные числа используются для решения графических задач, построения графиков функций и анализа геометрических фигур. Например, координатные числа позволяют определить расстояние между двумя точками на плоскости, найти середину отрезка, определить угол между двумя векторами и т.д.
Физика:
В физике координатные числа используются для описания положения, скорости и ускорения движущихся объектов. Координатные числа позволяют выразить законы физики в математической форме и провести анализ движения тела. Например, при описании движения автомобиля на дороге, используются координатные числа для определения его положения на плоскости, скорости и ускорения.
География:
В географии координатные числа используются для определения географического положения местности. Широта и долгота являются координатными числами, которые используются для определения точного местоположения на поверхности Земли. Эта информация необходима для навигации, составления карт, изучения климата и географических особенностей.
Инженерия:
В инженерии координатные числа используются для проектирования, измерения и построения объектов. Например, при строительстве зданий используются координатные числа для определения положения стен, окон и дверей. Координатные числа также используются в компьютерном моделировании для создания трехмерных моделей и визуализации реальных объектов.
Примеры координатных чисел:
- Точка на плоскости с координатами (3, 4) имеет x-координату 3 и y-координату 4.
- Точка в пространстве с координатами (1, 2, 3) имеет x-координату 1, y-координату 2 и z-координату 3.
- Широта и долгота (координаты) определяют географическое положение на поверхности Земли.
- Параметры движения автомобиля, такие как скорость и ускорение, могут быть представлены как координатные числа в зависимости от времени.
- Построение графика функции y = f(x) подразумевает использование координатных чисел для построения точек на плоскости.
- Трехмерная модель здания может быть представлена как набор точек с координатными числами.
Вывод:
Координатные числа играют важную роль в различных областях, где требуется определение позиции и взаимодействия объектов. Они предоставляют систему для анализа и визуализации различных параметров, открывая возможности для более глубокого изучения и понимания окружающего мира.
Приложения
Декартовы координаты — это абстракция, которая имеет множество возможных приложений в реальном мире. Однако для наложения координат на проблемное приложение используются три конструктивных шага. 1) Необходимо выбрать единицы расстояния, определяющие пространственный размер, представленный числами, используемыми в качестве координат. 2) Начало координат должно быть назначено конкретному пространственному положению или ориентиру, и 3) ориентация осей должна быть определена с использованием доступных ориентиров для всех осей, кроме одной.
Рассмотрим в качестве примера наложение трехмерных декартовых координат на все точки на Земле (то есть геопространственное трехмерное изображение). Какие единицы имеют смысл? Километры — хороший выбор, поскольку первоначальное определение километра было геопространственным — 10 000 км равнялись расстоянию на поверхности от экватора до Северного полюса. Где разместить происхождение? Основываясь на симметрии, гравитационный центр Земли предполагает естественный ориентир (который можно обнаружить с помощью спутниковых орбит). Наконец, как сориентировать оси X, Y и Z? Ось вращения Земли обеспечивает естественную ориентацию, тесно связанную с принципом «вверх-вниз», поэтому положительное значение Z может принимать направление от геоцентра к Северному полюсу. Местоположение на экваторе необходимо для определения оси X, а нулевой меридиан выделяется как справочная ориентация, поэтому ось X принимает ориентацию от геоцентра до 0 градусов долготы, 0 градусов широты.
Обратите внимание, что при трех измерениях и двух ориентациях перпендикулярных осей, закрепленных для X и Z, ось Y определяется первыми двумя вариантами. Чтобы подчиняться правилу правой руки, ось Y должна указывать из геоцентра на 90 градусов долготы и 0 градусов широты
Так каковы геоцентрические координаты Эмпайр-стейт-билдинг в Нью-Йорке? С долготы -73,985656 градусов, широты 40,748433 градуса и радиуса Земли 40 000 / 2π км и преобразования из сферических координат в декартовы вы можете оценить геоцентрические координаты Эмпайр-стейт-билдинг, (x, y, z) = (1330,53 км, –4635,75 км, 4155,46 км). GPS-навигация полагается на такие геоцентрические координаты.
В инженерных проектах решающее значение имеет согласование определения координат. Нельзя предполагать, что координаты заранее определены для нового приложения, поэтому знание того, как построить систему координат там, где ее нет, необходимо для применения мышления Рене Декарта.
В то время как пространственные приложения используют одинаковые единицы измерения по всем осям, в деловых и научных приложениях каждая ось может иметь разные единицы измерения (например, килограммы, секунды, фунты и т. Д.).). Хотя четырехмерные и многомерные пространства трудно визуализировать, алгебру декартовых координат можно легко расширить до четырех или больших чисел. (Этот вид алгебраического расширения используется для определения геометрии пространственных пространств.) И наоборот, бывает полезно использовать геометрию декартовых координат в двух или трех часто измерениях, чтобы визуализировать алгебраические отношения между двумя или тремя из многих непространственных пространств.
График функции или отношения — это набор всех точек, удовлетворяющих этой функции или отношению. Для функций одной функции f — это набор всех точек (x, y), где y = f (x) — график функции f. Для функций g двух чисел, множества всех точек (x, y, z), где z = g (x, y) — график функции g. Набросок графика такая функция или отношения будет состоять из всех ее относительных экстремумов, ее вогнутой и точки перегиба, любых точек разрыва и ее конечного поведения. Все эти термины более полно полно в исчислении. Такие графики полезны в исчислении, чтобы понять природу и поведение функции или отношения.
Координаты своими словами для детей
Координаты — это способ описать положение точки на плоскости или в пространстве с помощью чисел. Представь себе, что ты находишься на большом листе бумаги или в комнате со множеством игрушек. Если тебе нужно сказать другу, где находится какая-то игрушка или ты хочешь указать место, где находишься сам, ты можешь использовать координаты.
Для удобства, мы можем представить, что у листа бумаги или комнаты есть оси. Ось X идет горизонтально, а ось Y — вертикально. Точка с координатами (0,0) будет находиться в середине листа бумаги или комнаты. Если ты хочешь указать точку, которая находится правее середины листа бумаги или комнаты, ты используешь положительные числа для координаты X. Если точка находится левее середины, ты используешь отрицательные числа для координаты X. Аналогично, если точка находится выше середины, используются положительные числа для координаты Y, а если точка ниже середины — отрицательные числа.
Таким образом, каждая точка на плоскости или в пространстве имеет свои координаты, которые состоят из чисел. Ты можешь представить, что координаты — это адрес точки, который позволяет нам найти ее местоположение среди других точек. Например, если мы говорим, что точка находится в координатах (3,2), это означает, что она находится на трех шагах вправо от середины листа бумаги или комнаты и на два шага вверх от середины.
Таким образом, координаты позволяют нам описывать положение объектов и точек на плоскости или в пространстве с помощью чисел. Это очень полезно, потому что позволяет нам легко общаться о местоположении и перемещении объектов.
Используемая литература:1. Белова, Т.И. Вычисление неопределенных интегралов. Обыкновенные дифференциальные уравнения. Компьютерный курс: учеб. пособие / Т.И.Белова, А.А.Грешилов, И.В.Дубограй; Ред. А.А.Грешилов. — М.: Логос, 2004. — 184 с. + 1 эл. опт. диск (CD-ROM).2. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2006. — 432 с.3. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие / Г.Н.Берман. — 22-е изд., перераб. — СПб.: Профессия, 2005. — 432 с.4. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. для вузов. В 2 ч. Ч.1 / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 725 с.5. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч. 1. Дифференциальное и интегральное исчисление / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; Ред. В.А.Садовничий. — 3-е изд., испр. — М.: ДРОФА, 2001. — 725 с.6. Виноградова, И.А. Задачи и упражнения по математическому анализу: учеб. пособие для вузов. Ч.2. Ряды, несобственные интегралы, ряды Фурье, преобразование Фурье / И.А.Виноградова, С.Н.Олехник, В.А.Садовничий; ред. В.А.Садовничий . — 3-е изд., испр. — М.: ДРОФА, 2001. — 712 с.7. Голоскоков, Д.П. Уравнения математической физики. Решение задач в системе Maple: учеб. для вузов / Д.П.Голоскоков. — СПб.: Питер, 2004. — 538с.8. Гурова, З.И. Математический анализ. Начальный курс с примерами и задачами: учеб. для втузов / З.И.Гурова, С.Н.Каролинская, А.П.Осипова; Ред. А.И.Кибзун. — М.: Физматлит, 2002. — 351 с.9. Лукьянов, А.В. Обыкновенные дифференциальные уравнения: учеб. пособие по решению задач / А.В.Лукьянов, Ю.Д.Погуляев. — Челябинск: Полиграф-Мастер, 2006.10. Математический анализ в вопросах и задачах: учеб. пособие для вузов / В.Ф.Бутузов, Н.Ч.Крутицкая, Г.Н.Медведев, А.А.Шишкин; Ред. В.Ф.Бутузов . — 5-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 479 с.Значение термина Координаты на academic.ru
Ориентация и рука
В двух измеренийх
правой руки
Фиксация или выбор оси x определяет ось y до направления. А именно, ось y обязательно представляет собой , перпендикуляр оси x через точку, отмеченную 0 на оси x. Но есть выбор, какую из двух половинных линий на перпендикуляре обозначить как положительную, а какую как отрицательную. Каждый из этих двух вариантов определяет различную ориентацию (также называемую хиральностью) декартовой плоскости.
Обычный способ ориентирования плоскости с положительной осью X, направленной вправо, и положительной осью Y, направленной вверх (причем ось X является «первой», а ось Y — «второй» ось) признанной положительной или стандартной ориентацией, также называемой правой ориентацией.
Обычно используемый мнемоник для определения положительной ориентации — это правило правой руки. Поместите несколько сжатую правую руку на плоскость с большим пальцем вверх, указав от оси x к оси y в положительно ориентированной системе координат.
Другой способ ориентировать — это следовать правилам левой руки, положив левую руку на плоскость большим пальцем вверх.
Когда большой палец направлен от начала оси вдоль оси в положительную сторону, кривизна пальцев указывает на положительное вращение вдоль оси.
Независимо от правил, используемой для ориентации плоскости, вращение системы координат сохранит ориентацию. Переключение любых осей изменит ориентацию на обратную, но переключение оставит ориентацию сохранить.
В трех измеренийх
После задания осей x и y они определяют линию , вдоль которой должна лежать ось z, но есть две возможные ориентации для этой линии. Возникающие в результате двух возможных систем координат называются «правая» и «левая». Стандартная ориентация, при которой плоскость xy горизонтальна, а ось z направлена вверх (а ось x и y образуют положительно ориентированную двумерную систему координат в плоскости xy, если смотреть сверху на плоскость xy) называется правосторонней или положительной .
. Название происходит от правой руки. Если указательный палец правой руки направлен вперед, средний палец согнут под прямым углом к нему, а большой палец расположен под прямым углом для обоих пальца указывает относительную ориентацию осей x, y и z в правой системе. Большой палец указывает ось x, указательный палец — ось y, средний палец — ось z. И, если то же самое проделать левой рукой, получится наоборот левосторонняя система.
На рисунке 7 изображены левая и правая системы координат. Отображение трехмерного объекта на двухмерном изображении показано на рисунке. Ось, направленная вниз (и вправо), также есть для направления на наблюдателя, тогда как «средняя» ось для направления в сторону от наблюдателя. Красный круг параллелен горизонтальной плоскости xy и указывает вращение от оси x к оси y (в обоих случаях). Следовательно, красная стрелка проходит перед осью z.
Рисунок 8 — еще одна попытка изобразить правую систему координат. Опять же, возникает неоднозначность, вызванная проецированием трехмерной системы координат на плоскость. Многие наблюдатели видят рисунок 8 как «переворот» между выпуклым кубом и вогнутым «углом». Это соответствует двум возможным ориентациям пространства. Если смотреть на фигуру как выпуклую, это дает левую систему координат. Таким образом увидеть «правильный» способ просмотра рисунка 8 — представить ось x как указывающую в сторону наблюдателя и, таким образом, в изогнутом углу.
Целочисленный вектор
В дальнейшем мы много раз будем работать со структурами, определёнными схожим образом.
Можно было бы унаследоваться от класса квадрата или скруглённого квадрата , но
у него довольно много методов, в рамках обучения проще создать новую структуру ограниченной
системы координат. Такие системы координат помимо базисных векторов-ортов определяются ещё
и диапазоном допустимых значений каждой из координат.
Система координат окна как раз является
ограниченной, если считать, что всё, что выходит за границы окна не отображается.
Чтобы удобнее было работать с такой системой координат, определим в первую очередь класс двумерного
целочисленного вектора .
Подробно разбирать этот класс не будет. Методы в нём довольно тривиальны и задокументированы
Отдельно рассмотрим только конструктор и некоторые неочевидные методы
Я добавил конструктор от событий движка, чтобы из них можно было проще
получать координаты.
Также в методе, возвращающем случайный вектор в заданном диапазоне, используется
метод , обычно его рекомендуют использовать для многопоточных приложений,
но я советую сразу привыкать к нему, т.к. и в однопоточных приложениях он тоже
очень удобен. Чтобы использовать обычный рандом, нужно создавать объект класса и
уже работать с ним.
У части методов в описании добавилось новая команда . С её помощи описывается, что именно
возвращает документируемый метод.
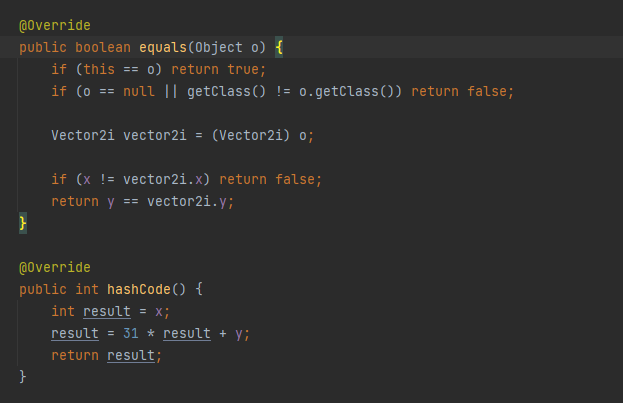
Рассмотрим подробно последние два метода.
отвечает за проверку на равенство двух объектов. Вначале мы проверяем особые случаи,
приводим объект к текущему классу, а потом уже выполняем все проверки.
В аргументах мы передаём объект именно класса , а не текущего, т.к. мы перегружаем
метод , а в родителе, т.е. в классе он определён с аргументом именно
.
Когда вы сами будете писать проверку, сравнивайте не все поля, а только
действительно важные. В данном случае поля всего два и оба важны при проверке на равенство.
Но дальше нам встретятся классы, у которых не нужно сравнивать все поля потому что они
либо служебные, либо определяются через другие поля.
Второй метод возвращает хэш объекта. О хэшах было рассказано в главах Git.
Эти два метода строятся всегда по одной и той же методике, поэтому в idea есть их автогенерация.
Для этого перевидите курсор внутрь класса, но снаружи методов и нажмите .
В появившемся меню выбираем .
В следующем окне нам нужно выбрать схему, согласно которой формируется документация. Мне больше
нравится документация по умолчанию от Intellij, но вы можете выбрать и другую. Они все работают,
а разница для данного проекта несущественна.
В следующем окне мы указываем, какие поля должны быть задействованы в методе
В следующем окне — в методе
сформирует новые методы за нас
Создайте новый коммит и отправьте его на сервер.
Линейные координаты: определение и обозначение
В системе линейных координат ось прямой обозначается как линия, на которой располагаются точки. Обычно, чтобы обозначить точку на оси координат, используются две прямоугольные системы, обозначенные как «х» и «у».
Ось «х» обозначает горизонтальное направление, причем точки, расположенные слева от нулевой точки «0» на оси «х», имеют отрицательные значения координат. Точки, расположенные справа от нулевой точки «0» на оси «х», имеют положительные значения координат.
Ось «у» обозначает вертикальное направление, причем точки, расположенные ниже нулевой точки «0» на оси «у», имеют отрицательные значения координат. Точки, расположенные выше нулевой точки «0» на оси «у», имеют положительные значения координат.
Таким образом, «х» и «у» представляют собой значения, которые выражают положение точки на прямой. Зная значения «х» и «у», можно точно определить положение точки в системе линейных координат.
СК, используемые на практике
Практическими реализациями пространственной геоцентрической земной системы координат являются системы координат WGS-84, ПЗ-90.11 и ГСК-2011.
Система координат WGS-84
WGS-84 (World Geodetic System (Всемирная геодезическая система координат)) – это система геодезических параметров Земли 1984 года, используемая в GPS, в число которых входит система геоцентрических координат).
Система координат ПЗ-90.11
ПЗ-90.11 (общеземная геоцентрическая система координат «Параметры Земли 1990 года») — это государственная система координат, используемая в ГЛОНАСС.
ПЗ-90.11 была установлена постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования в целях геодезического обеспечения орбитальных полетов, решения навигационных задач и выполнения геодезических и картографических работ в интересах обороны Российской Федерации.
Система координат ГСК-2011
ГСК-2011 (геодезическая система координат 2011 года) – это государственная система координат, установленная постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования при осуществлении геодезических и картографических работ на территории Российской Федерации.
Система координат МСК
МСК – это местная система координат субъекта Российской Федерации, установленная для целей обеспечения проведения геодезических и картографических работ при осуществлении градостроительной и кадастровой деятельности, землеустройства, недропользования и иной деятельности.
Каждый субъект имеет свою МСК с номером данного субъекта, например, местная система координат Московской области именуется МСК-50.
Архивные системы координат
Существуют архивные системы координат, которые в настоящее время не используются (не действуют).
Среди них можно выделить:
- СК-42 – система координат 1942 года, введенная постановлением Совета Министров СССР от 7 апреля 1946 года №760 в качестве единой государственной системы координат при выполнении геодезических и картографических работ.
- СК-63 – система координат 1963 года, предназначенная для создания топографических и специальных карт гражданского применения, а также для решения народнохозяйственных задач на территории Советского Союза. Отменена Постановлением ЦК КПСС и СМ СССР от 25 марта 1987.
- СК-95 – система координат 1995 года, установленная постановлением Правительства Российской Федерации от 28 июля 2000 года №568 в качестве единой государственной системы координат при выполнении геодезических и картографических работ.
Альтернативные схемы адресации
Было предпринято несколько попыток разработать эффективные системы координат для гексагональной сетки. Снайдер описывает систему координат, основанную на неортогональных базисах, которая называется системой h2 . Она разработала интересную трехкоординатную систему, в которой используется наклонная плоскость в трехмерном пространстве. По разным причинам оба этих подхода требуют громоздких машинных представлений, что приводит к неэффективным операциям обработки изображений. Общая сбалансированная троичная система (GBT) основана на иерархии ячеек, где на каждом уровне каждая ячейка представляет собой совокупность ячеек с предыдущего уровня. В двух измерениях GBT может использоваться для адресации гексагональной сетки, где каждая точка сетки адресуется строкой из семи цифр, и каждая цифра указывает положение шестиугольника на этом уровне иерархии. Использование GBT и слегка модифицированных версий GBT, таких как HIP и Spiral Architecture, для адресации гексагональных сеток в двух измерениях, широко распространено в литературе. Хотя эти подходы обладают некоторыми интересными математическими свойствами, они не могут быть удобными или эффективными для обработки изображений.
Координатная ось — «фотография» чисел в виде точек на прямой ##
пробa Координатная ось и координатная плоскость нужны для того, чтобы связать местность, точку пространства с числом или упорядоченной парой чисел. Такая связь используется давно. Например, на дороге ставят указатель расстояния до какого-либо объекта, месторасположение которого характеризуется одним числом. Математики разработали модель, удобную для описания любой прямолинейной дороги – это координатная ось.
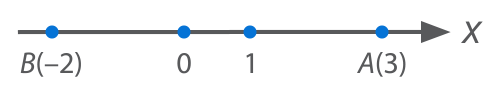
Чтобы из любой прямой получить координатную ось ,необходимо выбрать на ней нулевую точку$0$- это будет началом отсчета ;отметитьточку$1$ — определить единичный отрезок(т.е. выбрать масштаб)инарисовать стрелочку в положительном направлении отсчёта .На координатной оси изображается взаимооднозначные соответствия между точками и числами . Например, числу$3$на координатной прямойсопоставляется единственная точка$A$, точке$B$-единственное число$-2$, такое число назвали координатой.
Координатная прямая — это прямая с указанными на ней началом отсчёта O (0) , направлением и единичным отрезком.
пробa Математиками также была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале), так как известно, что в билете указывается номер ряда и номер места, то есть пара чисел, в которой номера упорядочены. Такая модель получила название координатная плоскость. Мы будем изучать координатную плоскость с прямоугольной системой координат.
Координаты точек на прямой.
пробa Точка$O$разбиваетпрямую$AB$на два луча$OA$и$OB$ . Если примем точку$O$ за начало отсчета , выберем на ней единичный отрезок и положительное направление , то мы превратим эту прямую в координатную ось .Рассмотрим на ней произвольную точку .Как определить ее положение?Для ответа на этот вопрос придумали понятие — координата . Положение любой точки на координатной осизадается её координатой.Чтобы отличить друг от друга координаты , перед числами на левом луче$OA$условились ставить знак «минус », а перед числами на правом луче$OB$-знак«плюс».

Координатысо знаком»$-$»называются отрицательными.Координатысо знаком «+» называютсяположительными .
Точка$O$- начало отсчета илиначало координат , изображает ноль.Само число$0$не является ни положительным ни отрицательным , только отделяет положительные и отрицательные числа друг от друга .
Координата точки — это число , показывающее положение точки на прямой.
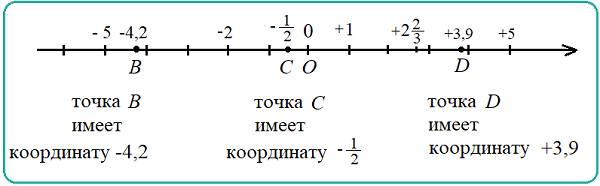
Записывают координаты точек$B$,$C$,$D$следующим образом:$B(-4,2)$,$C\left(-\frac{1}{2}\right)$,$D(3,9)$.
Изображение чисел точками на координатной оси.
Числа на координатной прямой выглядят точками. Для тогочтобыпостроитьточку, соответствующую некоторому числу$a$ , нужно:определить знак этого числа ;от начала координат отложить отрезок , равный$\left|a\right|$вправо , если знак»+»ивлево , еслизнак»-» .
Число$a$в таком случае называют координатой построенной точки .
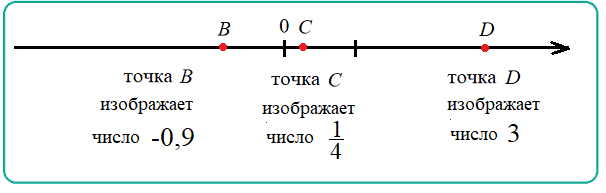
На рисунке числа $3$, $\frac{1}{4}$,$-0,9$изображены соответсвенно точками$B$,$C$,$D$. Числа- это«адреса»точек на координатной прямой.Точки-это»фотографии» чисел.
Введение оси координат:
1) Выбрать на прямой начало координат;
2) Выбрать положительное направление;
3) Выбрать единичный отрезок.
Координаты точки:
Каждой точке можно присвоить свою координату-это расстояние от точки до начала координат с учетом знака: слева от $0$знак $-$ , справа$+$.
Изображение числа : пробa
По любой координате можно восстановить точку.
























