Степени с рациональными показателями
Степени с действительными показателями. Будем, как и в п. 11, рассматривать только корни из положительных чисел. Мы видели, что в случае, когда m делится нацело на n,
Обобщая это правило, можно ввести следующее определение степени с положительным рациональным показателем p/q:
![]()
В случае отрицательного рационального показателя степени —p/q полагают (по аналогии со случаем целого отрицательного показателя степени)
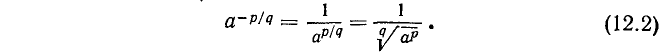
На степени с рациональными показателями распространяются все правила действий над степенями с натуральными и вообще целыми показателями. Для их обоснования достаточно применить правила п. 11 действий над корнями. Докажем, например, свойство
Имеем
Так же получим Отсюда
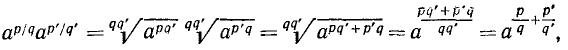
что и требовалось доказать.
Рассматривают также степени положительного числа а при произвольных действительных показателях. В основу определения при иррациональном х кладется последовательное приближение х рациональными числами. Так, например, для следует рассмотреть приближения по недостатку и по избытку для и возводить 3 в соответствующие рациональные степени, записывая
По мере продолжения этого процесса левая и правая части неравенств, выраженные бесконечными десятичными дробями, будут иметь все большее и большее число совпадающих десятичных знаков, которые и будут приниматься за десятичные знаки, определяющие иррациональное число . Более подробно рассматривать этот вопрос мы не можем, но отметим, что имеет действительное вполне определенное значение при а > 0 и любом действительном х.
Замечание:
Извлечение корня нечетной степени возможно и из отрицательного числа. Поэтому выражению при а < 0 также можно приписать смысл с помощью равенства в случае, когда несократимая рациональная дробь p/q имеет нечетный знаменатель. В случае четного q и для иррациональных значений показателя степень отрицательного основания не определяется. Нуль в любой положительной степени равен нулю; нулевая и отрицательные степени нуля не определены.
Пример:
Произвести действия, пользуясь отрицательными и дробными показателями степени: .
Решение:
![]()
Характеристика верхнего индекса в математике
Верхний индекс может использоваться для обозначения степени, порядка, номера или других важных параметров. Он может указывать на количество повторов, множители, величину или другие характеристики, которые являются ключевыми для понимания задачи или формулы.
Например, в математических выражениях верхний индекс может быть использован для обозначения степени числа. Если у нас есть число 2 и верхний индекс 3, это означает, что число 2 возводится в куб.
У верхнего индекса также есть свои правила использования и соглашения. Например, в алгебре и арифметике верхний индекс пишется над основанием без скобок или других разделителей. Это помогает отличить верхний индекс от других символов или операций.
Верхний индекс также может быть использован в сочетании с нижним индексом. В таком случае, верхний индекс указывает на характеристику или свойство, а нижний индекс обозначает элемент или объект, к которому это свойство относится.
Использование верхнего индекса в математике позволяет уточнить и объяснить определенные аспекты выражений, формул и задач. Он делает математические концепции исчерпывающими и ясными, что обеспечивает более точное понимание математических операций и их результатов.
Свойства арифметического квадратного корня
Для упрощения некоторых выражений необходимо использовать особые правила работы с корнями. Сформулируем первое из них:
Математически это правило записывается так:
Например:
Тождество работает для любого количества множителей, а также в обратную сторону:
Однако следующее преобразование недопустимо:
Дело в том, что под знаком радикала не может быть отрицательное число! Слева под двумя радикалами стоят отрицательные числа, а справа под корнем находится уже положительная величина (– 2)•(– 32) = 64. В результате выражение слева не имеет смысл, а справа – имеет, поэтому знака равенства между ними быть не может.
Докажем это правило. Для этого возведем во вторую степень выражение
Получили, что по определению корня можно записать:
Следующее свойство касается дробей:
Символически это выглядит так:
Приведем примеры использования этого свойства:
Теперь докажем это правило. Можно записать, что
Значит, по определению верно равенство
Третье правило помогает извлекать корень из числа, возведенного в степень:
где а –действительное число (в том числе и отрицательное), а k – натуральное число.
Это тождество помогает выполнить следующие действия:
Стоит обратить внимание, что в последнем случае под корнем НЕ стоит отрицательное число, так как на самом деле (– 2)10 – это положительное число. Вообще при возведении любого числа в четную степень получается неотрицательное число
Для доказательства этого факта используем то, что
Зная это, можно выполнить преобразования:
Число перед корнем как стилистическое средство
В русском языке число перед корнем может указывать на количество, интенсивность или степень каких-либо качеств
Оно позволяет усилить выразительность слова и обратить на себя внимание слушателя или читателя
Например, слово «трикратный» становится более эмоционально окрашенным и сильным, чем обычное слово «кратный». Число «три» перед корнем придает ему значение «трехкратный», подчеркивая интенсивность.
Также, число перед корнем может использоваться для создания ритмической и мелодичной структуры фразы или стихотворения. Оно добавляет музыкальности и гармоничности в речь.
Более того, число перед корнем может использоваться в качестве метафорического или символического способа передачи информации. Например, число «сто» перед корнем может олицетворять большое количество чего-либо, а число «тысяча» — еще большее число. Такие слова вносят дополнительные оттенки смысла в текст и вызывают живое восприятие.
Важно отметить, что использование числа перед корнем требует аккуратности и соблюдения стилистической меры. Чрезмерное использование этого средства может привести к банальности или преувеличению смысла
Поэтому важно учитывать контекст и цель речи при его использовании.
В итоге, число перед корнем является важным стилистическим средством, позволяющим усилить эмоциональную нагрузку, создать ритмичность и мелодичность, а также добавить дополнительные оттенки смысла в слово или фразу.
Что такое арифметический квадратный корень
А почему же число \( a\) (число под корнем) должно быть обязательно неотрицательным?
Например, чему равен \( \sqrt{-9}\)?
Так-так, попробуем подобрать. Может, три?
Проверим: \( {{3}^{2}}=9\), а не \( -9\).
Может, \( \left( -3 \right)\)?
Опять же, проверяем: \( {{\left( -3 \right)}^{2}}=9\).
Ну что же, не подбирается?
Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!
Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!
Ведь в определении сказано, что «квадратным корнем из числа\( a\)называется такое неотрицательное число, квадрат которого равен\( a\)».
Но подождите! В самом начале мы разбирали пример \( {{x}^{2}}=4\) и один из ответов был отрицательным числом!
Мы подбирали числа, которые можно возвести в квадрат и получить при этом \( \displaystyle 4\). Ответом были \( \displaystyle 2\) и \( \displaystyle -2\)
А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?
Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.
К примеру, \( \displaystyle {{x}^{2}}=4\) (квадратное уравнение) не равносильно выражению \( x=\sqrt{4}\) (арифмитический квадратный корень).
Из \( {{x}^{2}}=4\) следует, что
\( \left| x \right|=\sqrt{4}\), то есть \( x=\pm \sqrt{4}=\pm 2\) или \( {{x}_{1}}=2\); \( {{x}_{2}}=-2\)
(не помнишь почему так? Почитай тему «Модуль числа»!)
А из \( x=\sqrt{4}\) следует, что \( x=2\).
Конечно, это очень путает, но это необходимо запомнить, что знаки «плюс-минус» являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.
В наше квадратное уравнение подходит как \( 2\), так и \( x=-2\).
Вопрос-ответ:
Что такое корень в математике?
Корень — это одно из основных арифметических действий, которое позволяет найти число, умноженное на себя, равное заданному числу. Например, корень квадратный из 25 равен 5, так как 5 умноженное на 5 дает 25.
Как отличить знак корня от знака деления?
Знак корня имеет форму радикала, который состоит из горизонтальной линии и выступающего из нее вертикального отрезка. Знак деления обозначается чертой, которая проходит непосредственно между числителем и знаменателем.
В каких случаях используют знак корня?
Знак корня используется, когда мы хотим найти значение числа, возведенного в определенную степень. В математике корень часто используется при решении квадратных и других уравнений, в геометрии — для вычисления площади окружности, объема шара и т. д.
Как извлечь корень из отрицательного числа?
Извлечение корня из отрицательного числа не имеет решения в области действительных чисел. В этом случае используются комплексные числа, но их рассмотрение лежит за рамками статьи.
Как найти корень заданного числа?
Для нахождения корня из числа необходимо применить соответствующую математическую операцию. Корень квадратный из числа можно найти путем извлечения из этого числа квадратного корня. Для извлечения корня в MATLAB используется функция sqrt(x), а в Python — math.sqrt(x), где x — число, из которого необходимо извлечь корень.
Чем отличается корень n-ой степени от корня квадратного?
Корень квадратный (n=2) извлекает квадрат числа, а корень n-ой степени (n>2) — его n-ую степень. То есть, если корень квадратный извлекает квадрат числа, то корень кубический уже извлекает куб этого числа. Также, при извлечении корня n-ой степени мы получаем n возможных значений, в то время как корень квадратный имеет всего два значения — положительный и отрицательный.
Можно ли использовать корень в компьютерных программах?
Да, корень — это математическая операция, которая может быть использована в компьютерных программах. В языках программирования, таких как MATLAB и Python, есть соответствующие функции для извлечения корня из числа. Также корень может быть использован для решения уравнений и других задач в области науки и техники.
Поразрядное нахождение значения корня
Мы разобрали несколько методов, которые вы можете выбрать на своё усмотрение. Однако, есть еще один, который может понадобиться в таких ситуациях, когда нужно знать полное значение корня, а число, находящееся под корнем нельзя представить в виде n-ной степени определенного числа.
Для таких случаев существует алгоритм поразрядного нахождения значения корня, который нужно использовать, чтобы получить нужное количество значений определяемого числа.
Пример 1:
Итак, чтобы в этом разобраться, найдем значение квадратного корня из 7:
1. Находим значение разряда единиц, перебирая значения 0, 1, 2, …, 9, в это же время вычисляя их во 2 степени до нужного значения, которое больше подкоренного числа 7. Значение ряда единиц равняется 2 (потому как 2² < 7, а 2³ > 7).
2. Следующий на очереди — разряд десятых. Здесь мы будем возводить в квадрат числа: 2.0, 2.1, 2.2, …, 2.9, сравнивая результат с нужным нам числом 7. Так как 2.6² < 7, а 2.7² > 7, то значение десятых равняется 6.
3. Значение сотых. По аналогии находим приближенное значение к 7.
2.64² = 6,9696 подходит нам, так как 2.65²=7.0225, а это больше 7. Действуя таким же образом, можно и дальше находить значение √7 ≈ 2.64.
Теперь, когда мы разобрались с извлечением корней, перейдем к практике. Специально для вас составлены задания с ответами, чтобы вы попробовали воспользоваться приобретенными знаниями. Решайте без таблиц и калькулятора.
Задания для отработки материала
1 задание
а)√324
б)√900
в)√1369
2 задание
а)³√531,441
б)³√166,375
3 задание
а) ⁵√-14 2471/1024
б) ⁵√-5 1182/3125
4 задание
а)Найдите квадратный корень из 3.
б)Найдите квадратный корень из 5.
в)Найдите квадратный корень из 9.
Ответы с решением
1 задание
а)√324
1)2×2×3×3×3×3=2²×3⁴=√324, а чтобы извлечь, мы умножаем:
2)2×3×3=18. Получается, √324=18.
б)√900
1)2×2×3×3×5×5=2²×3²×5²=√900.
Извлекаем:
2)2×3×5=30. Мы получили √900=30.
в)√1369
1)37×37=37²=√1369.
А здесь мы оставляем 37, так как это единственное число в квадрате. Конечным ответом будет: √1369=37.
2 задание
а)³√531441.
1)3×3×3×3×3×3×3×3×3×3×3×3=3¹²=³√531441.
Разложили на простые множители, а теперь найдем квадратный корень.
2)3¹² это 3×3×3×3, т.к. 3 у нас в 12 степени. Это можно проверить, отняв из 12 столько троек, чтобы вышел 0: 12-3-3-3-3. Так что, 3⁴=81; ³√531441=81.
3)1000=10³.
4)³√531441/³√1000=81/10=8,1.
б)³√166,375.
1) 5×5×5×11×11×11=5³×11³=³√166375.
2)5³×11³=55. Так как числа в кубе – они в степени 1.
3) 1000=10³.
4)³√166375/³√1000=55/10=5,5.
3 задание
а)
1) ⁵√-14 2471/1024 = -⁵√14 2471/1024.
2) -⁵√14 2471/1024= -⁵√16801/1024.
3) -⁵√16801/1024 = — ⁵√16801/⁵√1024.
4) ⁵√16801/⁵√1024 = — ⁵√6⁵/⁵√4⁵ = — 6/4 = — 1,5.
б)
1) ⁵√-5 1182/3125 = -⁵√5 1182/3125.
2) -⁵√5 1182/3125= -⁵√16807/3125.
3) -⁵√16807/3125 = — ⁵√16807/⁵√3125.
4) ⁵√16807/⁵√3125 = — ⁵√7⁵/⁵√5⁵ = — 7/5 = — 1,4.
4 задание
а)√3≈1,73.
б√5≈2,23.
в)√8≈2,82.
Извлечение квадратного корня из большого числа
Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.
Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:
- Определить «сотни», между которыми оно стоит.
- Определить «десятки», между которыми оно стоит.
- Определить последнюю цифру в этом числе.
Извлечь корень из большого числа можно разными способами — вот один из них.
Извлечем корень из √2116.
Наша задача в том, чтобы определить между какими десятками стоит число 2116.
102 = 100
202 = 400
302 = 900
402 = 1600
502 = 2500
Мы видим что, 2116 больше 1600, но меньше 2500.
Это значит, что число 2116 находится между 402и 502.
41, 42, 43, 44, 45, 46, 47, 48, 49.
Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.
Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей
12 = 1
22 = 4
32 = 9
42 = 16 ⇒ 6
52 = 25 ⇒ 5
62 = 36 ⇒ 6
72 = 49 ⇒ 9
82 = 64 ⇒ 4
92 = 81 ⇒ 1
Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.
Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.
Число 43, возведенное в квадрат, даст число, на конце которого — 9.
Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.
Таким образом, у нас остаются два варианта: 442 и 462.
Далее вычисляем: 44 * 44 = 1936.
46 * 46 = 2116.
Ответ: √2116 = 46
Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат.
Еще пример. Извлечем корень из числа √11664
Разложим число 11664 на множители:
11666 : 4 = 2916
2916 : 4 = 729
729 : 3 = 243
243 : 3 = 81
| 11664 | 4 |
| 2916 | 4 |
| 729 | 3 |
| 243 | 3 |
| 81 | 81 |
Запишем выражение в следующем виде:
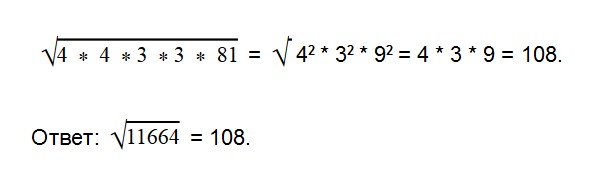
Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.
Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
- Вычислите значение квадратного корня: √36
- Вычислите значение квадратного корня: √64*36
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение квадратного корня:
- Вычислите значение выражения: 4√16 — 12
- Вычислите значение выражения: 5√9 — 8
- Вычислите значение выражения: 7√25 — 10
- Вычислите значение квадратного корня:
- Вычислите значение квадратного уравнения:
- Вычислите значение квадратного уравнения:
- Извлеките квадратный корень из числа √7056 удобным вам способом
Как решаем:7056 4 1764 4 441 3 147 3 49 7 7 7 1 - Вычислите значение квадратного корня √0,81
Ответ: √0,81 = 0,9 - Вычислите значение квадратного корня:
Как решаем:
= 0,09 - Вычислите значение выражения: 8√81 — 20
Как решаем: 8√81 — 20 = 8 * 9 — 20 = 72 — 20 = 52
Ответ: 8√81 — 20 = 52. - Вычислите значение выражения: 13√100 — 15
Как решаем: 13√100 — 15 = 13 * 10 — 15 = 130 — 15 = 115
Ответ: 13√100 — 15 = 115. - Вычислите значение выражения: √16 + 5√4
Как решаем: √16 + 5√4 = 4 + 5 * 4 = 4 + 20 = 24 Ответ: √16 + 5√4 = 24. - Вычислите значение выражения: √36 + 2√9
Как решаем: √36 + 2√9 = 6 + 2 * 3 = 6 + 6 = 12
Ответ: √36 + 2√9 = 12. - Вычислите значение выражения: 2√16 — 3√25
Как решаем: 2√16 — 3√25 = 2 * 4 — 3 * 5 = 8 — 15 = -7
Ответ: 2√16 — 3√25 = -7. - Вычислите значение выражения: 3√81 — 5√9
Как решаем: 3√81 — 5√9 = 3*9 — 5 * 3 = 27 — 15 = 12
Ответ: 3√81 — 5√9 = 12. - Вынесите множитель из-под знака корень: √60
Как решаем: √60 = √15 * √4 = 2√15
Ответ: √60 = 2√15. - Вынесите множитель из-под знака корень: √160
Как решаем: √160 = √16 * √10 = 4√10
Ответ: √160 = 4√10. - Внесите множитель под знак корня: 6√7
Как решаем: √62 * 7 = √36 * √7 = √252
Ответ: 6√7 = √252. - Внесите множитель под знак корня: 8√2
Как решаем: 8√2 = √82 * 2 = √64 * √2 = √128 Ответ: 8√2 = √128. - Внесите множитель под знак корня: 9√5
Как решаем: 9√5 = √92 * 5 = √81 * √5 = √405
Ответ: 9√5 = √405. - Упростите выражение: (5 — √2)2
Как решаем: (5 — √2)2 = 52 — 2 * 5 * √2 + (√2)2 = 25 — 10√2 + 2 = 27 — 10√2.
Ответ: (5 — √2)2 = 27 — 10√2. - Вычислите значение выражения: 3√49 — 3√25
Как решаем: 3√49 — 3√25 = 3 * 7 — 3 * 5 = 21 — 15 = 6
Ответ: 3√49 — 3√25 = 6. - Вычислите значение квадратного корня: √484 * √576
Как решаем: √484 * √576 = 22 * 24 = 528
Ответ: √484 * √576 = 528. - Вычислите значение квадратного корня: √625 * √81
Как решаем: √625 * √81 = 25 * 9 = 225
Ответ: √625 * √81 = 225. - Найдите значение выражения: 3√100 — √144
Как решаем: 3100 — 144 = 3 * 10 — 12 = 18
Ответ: 3√100 — √144 = 18.
Преобразование выражений с квадратными корнями
Изученные правила помогают преобразовывать некоторые выражения. Так, можно вынести множитель из-под знака корня:
Это действие может использоваться для сложения корней, у которых, казалось бы, стоят разные числа под знаком радикала:
![]()
Обратное действие называют внесением множителя под знак корня:
![]()
Пример. Какое число больше
Решение. Внесем множитель под знак корня:
Из двух корней больше тот, у которого больше подкоренное выражение, поэтому
Из этого следует, что
Заметим, что под знак радикала может быть внесен исключительно неотрицательный множитель! Знак минуса должен остаться перед радикалом:
Принято считать, что с дробью, содержащей радикал, проще работать, когда этот радикал находится в числителе, а не знаменателе. В связи с этим стремятся избавиться от иррациональности в знаменателе. В простейшем случае дробь просто домножают на квадратный корень:
Как видим, корень «переехал» из знаменателя в числитель. Несколько сложнее производится освобождение от иррациональности, если в знаменателе стоит сумма или разность корней. В этом случае помогает формула :
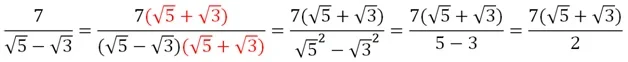
Рассмотрим несколько задач.
Пример. Найдите наибольшее значение выражения
Решение. По формуле разности квадратов можно записать:
Зная это, заменим знаменатель дроби:
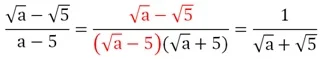
Эта дробь принимает наибольшее значение тогда, когда ее числитель, наоборот, принимает минимальное значение. Это произойдет при а = 0, так как арифметический квадратный корень не может быть отрицательным. Тогда наибольшее значение дроби будет составлять
Пример. Упростите выражение
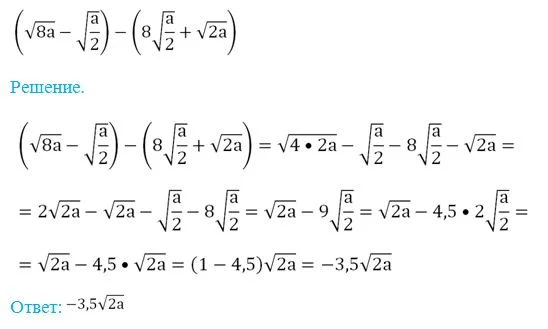
Довольно тяжелым является случай, когда под знаком корня находится другой корень. Выражения вида
называют двойным радикалом.
Существует формула двойного радикала, с помощью которой его можно иногда упростить:
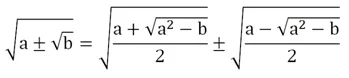
Для доказательства справедливости этого тождества возведем его правую часть в квадрат, используя (х ± у)2 = х2 ± 2ху + у2:
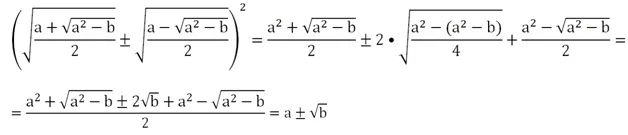
Принципиально важно, что величина а2 – b должна быть неотрицательной. Рассмотрим преобразование двойных радикалов на примере
Пусть надо освободиться от внешнего радикала в выражении
Для этого сначала внесем двойку под знак внутреннего радикала, а потом воспользуемся формулой:
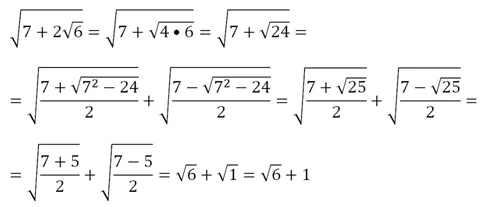
Заметим, что формула двойного радикала полезна в том случае, если выражение а2 – b является полным квадратом.
Квадратные корни
Вторая таблица — это таблица квадратных корней:
| √x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1,41421 | 1,73205 | 2 | 2,23607 | 2,44949 | 2,64575 | 2,82843 | 3 | ||
| 1 | 3,16228 | 3,31662 | 3,4641 | 3,60555 | 3,74166 | 3,87298 | 4 | 4,12311 | 4,24264 | 4,3589 |
| 2 | 4,47214 | 4,58258 | 4,69042 | 4,79583 | 4,89898 | 5 | 5,09902 | 5,19615 | 5,2915 | 5,38516 |
| 3 | 5,47723 | 5,56776 | 5,65685 | 5,74456 | 5,83095 | 5,91608 | 6 | 6,08276 | 6,16441 | 6,245 |
| 4 | 6,32456 | 6,40312 | 6,48074 | 6,55744 | 6,63325 | 6,7082 | 6,78233 | 6,85565 | 6,9282 | 7 |
| 5 | 7,07107 | 7,14143 | 7,2111 | 7,28011 | 7,34847 | 7,4162 | 7,48331 | 7,54983 | 7,61577 | 7,68115 |
| 6 | 7,74597 | 7,81025 | 7,87401 | 7,93725 | 8 | 8,06226 | 8,12404 | 8,18535 | 8,24621 | 8,30662 |
| 7 | 8,3666 | 8,42615 | 8,48528 | 8,544 | 8,60233 | 8,66025 | 8,7178 | 8,77496 | 8,83176 | 8,88819 |
| 8 | 8,94427 | 9 | 9,05539 | 9,11043 | 9,16515 | 9,21954 | 9,27362 | 9,32738 | 9,38083 | 9,43398 |
| 9 | 9,48683 | 9,53939 | 9,59166 | 9,64365 | 9,69536 | 9,74679 | 9,79796 | 9,84886 | 9,89949 | 9,94987 |
Почему число возводится в степень 2?
В математике степень два имеет особое значение и широко используется в различных областях. Возвести число в степень два означает умножить его само на себя. Такая операция называется возведением числа в квадрат и обозначается путем написания числа вверху и ниже над ним цифры 2.
Существует несколько причин, почему число возводится в степень 2. Во-первых, возведение числа в квадрат помогает в изучении и анализе различных моделей и закономерностей. Квадрат числа отражает его увеличение в два раза и позволяет лучше понять его изменения. Это особенно полезно в физике, где квадрат числа может представлять силу, энергию или площадь.
Во-вторых, возведение числа в квадрат широко используется в алгебре и математическом анализе. Например, такая операция может быть применена для нахождения корней уравнений или решения систем уравнений. Возвести число в степень 2 также позволяет производить различные преобразования и упрощения в выражениях, что упрощает их дальнейший анализ.
Кроме того, квадрат числа является неотрицательным значением. Возведение числа в степень 2 позволяет избавиться от отрицательных значений и сделать вычисления более удобными. Также, возведение в квадрат может использоваться для определения расстояний, площадей и объемов в геометрии.
В заключении, возведение числа в степень 2 является важной операцией в математике и наукам и широко используется для анализа, решения уравнений, моделирования и других целей. Квадрат числа отражает его изменение и может быть полезным средством для изучения и анализа различных явлений и закономерностей
Свойство корня как функции
На [0; +∞) можно поставить каждому числу х в соответствие единственное число корень n-степени из x при любом значении n.
То есть это означает, что на множестве [0; +∞) можно говорить о функции корня:
Теперь определим свойства функции корня и построим ее график.
Основные свойства корня как функции:
Промежуток [0; +∞) – является областью определения.
Так как неотрицательное число является корнем n-степени из неотрицательного числа, значит промежуток [0; +∞) будет областью значения функции.
Поскольку симметричным множеством не является область определения функции, поэтому данная функция не является ни нечетной, ни четной.
Операция по извлечению корня вводилась как обратная операция возведения в соответствующую степень.
Значит можно утверждать, что:

Теперь можно построить график функции корня.

Пользуясь графиком, можно записать оставшиеся свойства функции.
На промежутке [0; +∞) функция возрастает.
Сверху функция не ограничена, но она ограничена снизу, например, прямой у, которая = -0,5.
На всей области определения функция выпукла вверх.
У функции наименьшим значением будет являться 0, а наибольшего значения она не имеет.
Если в каждой из точек некоторого промежутка функция дифференцируема, то это значит, что на данном промежутке она непрерывна.
Тогда:
В любой точке промежутка [0; +∞) существует эта производная, исключением является только точка 0.
Поскольку в любой точке промежутка (0; +∞) функция имеет производную, значит на промежутке (0; +∞) функция дифференцируема.
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
 Область поиска арифметического корня — неотрицательные числа
Область поиска арифметического корня — неотрицательные числа
Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. Например, правило возведения в степень:
\{a}=\sqrt{{{a}^{k}}}\]
Обратите внимание: мы можем возвести подкоренное выражение в любую степень и одновременно умножить на эту же степень показатель корня — и в результате получится то же самое число! Вот примеры:
\{5}=\sqrt{{{5}^{2}}}=\sqrt{25} \\ & \sqrt{2}=\sqrt{{{2}^{4}}}=\sqrt{16} \\ \end{align}\]
Ну и что в этом такого? Почему мы не могли сделать это раньше? А вот почему. Рассмотрим простое выражение: $\sqrt{-2}$ — это число вполне нормальное в нашем классическом понимании, но абсолютно недопустимо с точки зрения арифметического корня. Попробуем преобразовать его:
$\begin{align} & \sqrt{-2}=-\sqrt{2}=-\sqrt{{{2}^{2}}}=-\sqrt{4} \lt 0; \\ & \sqrt{-2}=\sqrt{{{\left( -2 \right)}^{2}}}=\sqrt{4} \gt 0. \\ \end{align}$
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Действия с квадратным корнем, правила
При умножении корней важно помнить, что корень произведения равен произведению корней.
В задачах нередко требуется возвести корень в степень. Исходя из определения квадратного корня, при возведении числа, корень которого равен а, в квадрат, получится число а.
Простые задачи на возведение корня в квадрат не вызывают трудности. Чуть сложнее оказывается действие по возведению корня в другую степень. Для решения подобных заданий требуется применять свойства и правила действий со степенями.
Заметим, что вычисления выполнялись с четной степенью. Бывают варианты заданий с нечетными степенями. В таком случае, следует воспользоваться свойствами степени и разложить выражение на множители.
Когда степень больше, чем число 2, нужно вновь использовать свойства степеней.
После рассмотрения действий с корнями можно приступить к занесению чисел под знак корня.
Следует учитывать правило, согласно которому под знак квадратного корня допускается заносить лишь положительные числа.
Корни можно сравнивать. Такой навык пригодится при решении больших выражений, корнями которых являются иррациональные числа. Когда для получения интервала требуется расположить полученные решения на координатной прямой, без калькулятора сделать это сложно.
Рассмотрим последовательность действий для извлечения корней из больших чисел. В процессе необходимо разложить выражение под знаком корня и извлечь корень.
Действия с корнями: основы
Пример 1
650-28+512
Алгоритм действия:
Упростить подкоренное выражение. Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня
Обращаем ваше внимание, что второй множитель заносится под знак корня.
После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений
Нельзя складывать или вычитать подкоренные числа!
Пример 2
Давайте попробуем решить данный пример:
650=6(25×2)=(6×5)2=302. Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 302.
28=2(4×2)=(2×2)2=42. Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 42.
512=5(4×3)=(5×2)3=103. Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 103.
Результат упрощения: 302-42+103
302-42+103=(30-4)2+103=262+103.
Нужна помощь преподавателя?Опиши задание — и наши эксперты тебе помогут!Описать задание
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
Пример 3
(45)+45:
- Упрощаем (45). Раскладываем 45 на множители: (45)=(9×5);
- Выносим 3 из-под корня (9=3):45=35;
- Складываем множители у корней: 35+45=75.
Пример 4
640-310+5:
- Упрощаем 640. Раскладываем 40 на множители: 640=6(4×10);
- Выносим 2 из-под корня (4=2):640=6(4×10)=(6×2)10;
- Перемножаем множители, которые стоят перед корнем: 1210;
- Записываем выражение в упрощенном виде: 1210-310+5;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: (12-3)10=910+5.
Пример 5
95-23-45
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:
(9-4)5-23=55-23.
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.
- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3+(2x)1/2.
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
Интерпретация числа перед корнем
Число, стоящее перед корнем слова, имеет важное значение и может влиять на его толкование и смысл. Если число перед корнем отрицательное, это может указывать на отрицательные или противоположные характеристики, связанные с основным словом
Например, слова с отрицательным числом перед корнем могут быть связаны с негативными эмоциями, неприятными событиями или нежелательными результатами
Если число перед корнем отрицательное, это может указывать на отрицательные или противоположные характеристики, связанные с основным словом. Например, слова с отрицательным числом перед корнем могут быть связаны с негативными эмоциями, неприятными событиями или нежелательными результатами.
Наоборот, положительное число перед корнем может указывать на положительные или желательные характеристики, связанные с основным словом. Такие слова часто имеют связь с позитивными эмоциями, благоприятными событиями или желательными результатами.
Некоторые числа перед корнем могут иметь специальные значения и толкования. Например, число «один» перед корнем может указывать на уникальность, единство или первенство чего-либо. Число «два» может указывать на дуальность, пару или бинарность. Число «три» может быть связано с тройственностью, троичностью или некоторыми особыми свойствами.
Число перед корнем также может быть использовано для определения количества или меры, связанных с основным словом. Например, число «десять» перед корнем может указывать на большое количество, в то время как число «ноль» перед корнем может указывать на отсутствие или ничтожное значение.

























