Линейная регрессия. часть 1

Классификация числовых величин

Точка деления — это индивидуальный критерий, по которому можно заключить деление целого числа на другое значение. Следует отметить, что числа сортируются на два типа.

Для определения первого необходимо использовать три метода: специальные таблицы, вычислительные средства и вычислительные методы. Каждая книга по математике имеет первый номер в качестве приложения. Кроме того, специальные программы можно загрузить из Интернета. Это позволяет определить, находится ли значение в первом числе или нет.

Последний метод называется ручным, так как он требует использования точки разделения для определения принадлежности значения к данной группе. Отличие простой величины от сложной заключается в том, что она может быть разделена только с одной стороны или сама по себе. Комплексные значения включают значения, эквивалентные внешнему множителю единицы.

Эксперты рекомендуют записывать точки деления на специальных картонных карточках. Все правила для двух целых чисел должны быть им понятны. Новичкам, стремящимся преуспеть в этой отрасли, следует найти примеры каждого из них, как в случае с семеркой.

Классические примеры использования

Проверка на четность и нечетность

Одно из классических применений операции деления по модулю — проверка на четность или нечетность. В Python выражение n % 2 вернет 0, если число n четное, и 1, если оно нечетное.

Определение дня недели

Для определения дня недели можно использовать формулу Цонига — Гаусса: w = (d + 2*m + 3*(m+1)/5 + y + y/4 — y/100 + y/400 + 1) % 7, где d — день месяца, m — номер месяца (январь — 1, февраль — 2 и так далее), y — год (например, 2021). Результат деления по модулю на 7 даст номер дня недели (0 — воскресенье, 1 — понедельник и так далее).

Циклический сдвиг строки

Для циклического сдвига строки на k позиций можно использовать следующий код:

k = 3

s = s + s

print(s)

# выведет «efgabcd»

Здесь мы используем срез, чтобы разбить строку на две части — сдвинутую и оставшуюся. Затем мы склеиваем их в обратном порядке.

Поиск остатка от деления

Одно из главных применений деления по модулю — поиск остатка от деления (например, 7 % 3 = 1 или 10 % 4 = 2). Это дает возможность эффективно решать многие задачи, связанные с арифметикой и математикой в целом.

Проверка на четность и нечетность

В Python проверить, является ли число четным или нечетным, очень просто. Для этого используется оператор деления по модулю %, который возвращает остаток от деления двух чисел. Если число делится на 2 без остатка, то оно четное, в противном случае — нечетное.

Для проверки на четность можно использовать следующий код:

x % 2 == 0

— вернет True, если x четное

Для проверки на нечетность можно использовать следующий код:

x % 2 == 1

— вернет True, если x нечетное

Также можно использовать функцию divmod, которая возвращает результат деления и остаток в виде кортежа:

divmod(x, 2) == 0	— вернет True, если x четное
divmod(x, 2) == 1	— вернет True, если x нечетное

Важно учитывать, что оператор деления по модулю и функция divmod работают только с целыми числами, поэтому перед использованием необходимо привести число к целому типу, например:

x = int(input(«Введите число: «))

Также можно проверить четность и нечетность всех чисел в списке или кортеже, используя цикл:

for x in list:
 if x % 2 == 0:
  print(x, » — четное»)
 else:
  print(x, » — нечетное»)

Вывод на экран будет зависеть от того, какие числа содержатся в списке или кортеже и какая из проверок будет выполнена.

Вычисление контрольной суммы

Контрольная сумма — это целочисленное значение, которое вычисляется по определенному алгоритму на основе данных. Она используется для проверки целостности данных и обнаружения ошибок в передаче или хранении информации. В Python можно легко вычислить контрольную сумму с помощью различных алгоритмов.

Одним из наиболее распространенных алгоритмов вычисления контрольной суммы является алгоритм с использованием функции хэширования. В Python существует несколько встроенных функций хэширования, таких как sha1(), md5() и другие. Каждая из них имеет свой набор особенностей, но их цель одна — вычисление хэш-кода для заданных данных.

Еще одним способом вычисления контрольной суммы является использование операции деления по модулю. Она позволяет получить остаток от деления заданного числа на другое число. В Python операция деления по модулю представляется знаком процента (%). Например: 7 % 3 = 1. Это означает, что остаток от деления 7 на 3 равен 1.

Для вычисления контрольной суммы на основе операции деления по модулю можно пройтись по числам, которые нужно просуммировать, и вычислить сумму. Затем полученную сумму нужно разделить на определенное число, и остаток от этого деления будет являться контрольной суммой. Например: контрольная сумма для чисел 1, 2, 3, 4, 5 будет равна (1 + 2 + 3 + 4 + 5) % 10 = 5.

Таким образом, вычисление контрольной суммы в Python может быть достигнуто с помощью различных алгоритмов, и выбор того или иного зависит от цели вычислений и особенностей входных данных.

Необходимый признак сходимости числового ряда

Теорема. Если ряд сходится, то предел его общего члена при

равен нулю:

                        (17)

Следствие. Если предел общего члена ряда при

не равен нулю, то ряд расходится.

Пример 11. Используя необходимый признак сходимости, исследовать сходимость числового ряда

Решение. Общий член ряда

Найдём его предел при

Следовательно, данный ряд расходится.

Пример 12. Используя необходимый признак сходимости, исследовать сходимость числового ряда

Решение. Найдём предел общего члена ряда при

Так как (предел общего
члена не равен нулю), данный ряд расходится.

Установить сходимость ряда самостоятельно, а затем посмотреть решение

Пример 13. Используя необходимый признак сходимости,
установить, сходится ли ряд

.

Пример 14. Установить, сходится ли ряд

.

Пример 15. Записать первые пять членов числового ряда

и установить, сходится ли этот ряд.

Решение. Пять первых членов данного числового ряда:

Найдём предел общего члена ряда при

,

применяя дважды правило Лопиталя:

Так как (предел общего
члена равен нулю), данный ряд сходится.

Мы выяснили, что если числовой ряд сходится, то предел его общего члена равен нулю, а значит, выполняется условие (17).

Однако выполнение условия (17) не гарантирует сходимости числового ряда, оно не является достаточным для этого. Есть расходящиеся ряды, пределы общих членов которых при

равны нулю.

Примером такого ряда служит ряд (4):

который называется гармоническим. Последовательность его частичных сумм

монотонно возрастает, поскольку члены ряда положительны. Покажем, что она возрастает неограниченно. Для этого члены гармонического ряда, начиная с третьего, объединим в группы:

В первую включим два члена (3-й и 4-й), во вторую

члена (с 5-го по 8-й), в третью

членов (с 9-го по 16-й) и т.д, каждый раз увеличивая вдвое число членов в группе. Таких групп, очевидно, бесконечное множество. Если заменить члены ряда в каждой группе их последними членами, то сумма членов этой группы уменьшится и тогда справедливы неравенства

Сумма членов каждой группы больше 1/2, а сумма членов, включённых в достаточно большое число групп, как угодно велика. Следовательно, последовательность частичных сумм гармонического ряда неограниченно возрастает, а ряд расходится, хотя его общий член

при

стремится к нулю.

Заметим, что частичные суммы гармонического ряда возрастают хотя и ограниченно, но медленно.

Исследование сходимости ряда обычно начинают с проверки выполнения условия (17), чтобы сразу выделить расходящиеся ряды, для которых это условие не выполняется. Однако выполнение этого условия говорит лишь о том, что ряд может сходиться. Сходится он или расходится, должно показать дополнительное исследование с помощью достаточных признаков, рассмотрение которых дано в последующих урока раздела «Ряды».

Назад

Листать

Вперёд>>>

Всё по теме «Ряды»

• Числовые ряды
• Признак сравнения рядов
• Признак Даламбера сходимости рядов
• Радикальный признак Коши сходимости рядов
• Интегральный признак Коши сходимости рядов
• Знакочередующиеся и знакопеременные ряды. Признак Лейбница
• Функциональные ряды
• Степенные ряды
• Ряды Фурье

Советы и трюки

1. Используйте деление по модулю для проверки четности или нечетности числа. Если число делится на 2 без остатка, то оно четное, в противном случае — нечетное. Например:

• 4 % 2 == 0 — результатом будет True, так как число 4 четное.
• 7 % 2 == 1 — результатом будет True, так как число 7 нечетное.

2. Деление по модулю может использоваться для выделения последней цифры числа. Например, чтобы выделить последнюю цифру числа 123, можно использовать следующее выражение: 123 % 10, результатом будет 3.

3. Используйте деление по модулю для проверки делимости числа на другое число. Если результатом деления числа на другое число равен нулю, то первое число делится на второе без остатка. Например:

• 15 % 3 == 0 — результатом будет True, так как число 15 делится на 3 без остатка.
• 7 % 2 == 0 — результатом будет False, так как число 7 не делится на 2 без остатка.

4

При работе с отрицательными числами обратите внимание на то, как определяется остаток от деления. Он зависит от модуля делителя

Например, выражение -5 % 2 вернет -1, так как -5 можно представить в виде -2 * 2 + (-1), где -1 — это остаток от деления.

5. Используйте деление по модулю для циклического перебора элементов. Например, чтобы перебрать элементы списка по кругу, можно использовать такой код:

lst =	# список, который надо перебрать по кругу
i = 0	# начальный индекс
while True:	# бесконечный цикл
print(lst)	# выводим элемент с индексом i по модулю на длину списка
i += 1	# увеличиваем индекс для перехода к следующему элементу

Оптимизация производительности

Оптимизация производительности является одним из наиболее важных аспектов программирования. Использование деления по модулю в Python также требует оптимизации для повышения скорости работы программ. В этой статье мы рассмотрим основные методы оптимизации кода, использующего операцию деления по модулю в Python.

Одним из способов повышения производительности является максимальное использование встроенных функций и методов Python. Для деления по модулю рекомендуется использовать встроенную функцию divmod(). Она осуществляет деление сразу нацело, возвращая два значения: частное и остаток. Это позволяет избежать лишних операций и увеличить скорость работы программы.

Еще одним способом оптимизации производительности является использование циклов for и while вместо рекурсивных вызовов. Циклы for и while производят меньше накладных расходов и обычно работают быстрее. Также следует избегать лишних проверок условий, например, проверки на равенство числа нулю.

Использование битовых операций также может значительно повысить скорость работы программы. Например, операция & (побитовое И) может быть использована вместо операции % (деление по модулю), если все операнды являются степенями двойки.

Кроме того, можно уменьшить количество выполняемых операций путем использования кэширования результатов. Если часто используется операция деления по модулю с одним и тем же модулем, можно предварительно вычислить остатки и сохранить их в отдельном списке или словаре.

Используя эти методы, можно значительно увеличить производительность программы, работающей с операцией деления по модулю в Python. Также рекомендуется проводить тестирование и оптимизацию программы на большом объеме данных, чтобы убедиться в ее эффективности.

Работа с отрицательными числами

В Python, при делении отрицательного числа по модулю, результат может быть неожиданным. Это связано с тем, что при делении отрицательного числа на положительное, результат будет отрицательным.

Например, при делении -7 на 3, результатом будет -2, а не 1, как могло бы показаться. То есть, -7 % 3 = -2.

Однако, если оба числа отрицательные, результат будет положительным. Например, -7 % -3 = -1.

Для правильной работы с отрицательными числами в python, можно использовать функцию abs(), которая возвращает модуль числа. Таким образом, можно получить положительный результат.

Также, для более ясной работы с числами можно использовать модуль math, в котором есть функции для работы с числами, в том числе с отрицательными.

• math.ceil(x) — округляет число x до ближайшего большего целого;
• math.floor(x) — округляет число x до ближайшего меньшего целого;
• math.trunc(x) — удаляет дробную часть числа x;
• math.fabs(x) — возвращает модуль числа x.

Таким образом, для правильной работы с отрицательными числами в Python, нужно учитывать особенности деления по модулю, а также использовать функции из модуля math при необходимости.

Деление чисел с остатком через последовательное вычитание

Чтобы найти кутиент и остаток, мы можем прибегнуть к удалению делителя. Этот метод не всегда применим, но в некоторых случаях может быть очень полезен. Опять же, смотрите примеры.

Пример 2. Непрерывная абстракция наряду с балансом.

Теперь возьмите в руки семь яблок. Вы должны положить семь яблок в мешок по три яблока в каждом. Другими словами, разделите семь яблок на три.

Возьмите 3 яблока из первоначального количества и положите их в мешок. Таким образом, остается 7-3 = 4 яблока. Из оставшегося количества яблок снова извлеките 3 яблока и поместите их в другой пакет. Таким образом, они остаются 4-3 = 1 яблоко.

Одно яблоко — это остаток от деления. На этом этапе уже невозможно сформировать еще один мешок с тремя яблоками, и деление, по сути, завершено. Последствия разделения:.

Это означает, что число 3 каким-то образом дважды подходит к числу 7, причем один остаток меньше 3.

Рассмотрим другой пример. На этот раз мы приводим только математические данные, не прибегая к пропорциям.

Пример 3. Последовательное удаление в равновесии.

Число 99 больше 46, поэтому продолжите последовательное вычитание делителей.

Повторите эту функцию еще раз.

В результате, прежде чем взять остаток, необходимо было трижды отнять делимое от делителя. В результате получается меньше абстракций, чем делителей. В нашем случае остаток — это число 7.

Если делитель меньше делимого, последовательные абстракции не подходят. В этом случае ответ можно написать сразу. Неполный делитель равен нулю, а остаток равен делителю.

12 ÷ 36 = 0 (остаток 12) 47 ÷ 88 = 0 (остаток 47)

Следует также отметить, что что касается методов последовательной абстракции, то они полезны только тогда, когда все деление сводится к небольшому количеству вычитаний. Если дивиденд представляет собой множество делителей, использование этого метода невозможно и предполагает множество сложных вычислений.

Как удобнее всего вычислить частное

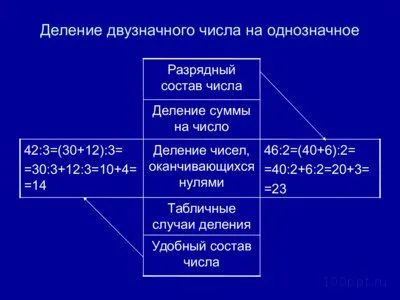
Деление — операция, обратная умножению. Поэтому в ряде случаев можно использовать таблицу умножения. Это называется табличным делением: оно возможно, если делимое является табличным значением, а делитель — однозначным числом. Так, если 3 * 5 = 15, то 15 : 3 = 5, а 15 : 5 = 3.

Если табличное деление не применимо, можно использовать деление в столбик, схема которого представлена на рисунке ниже.

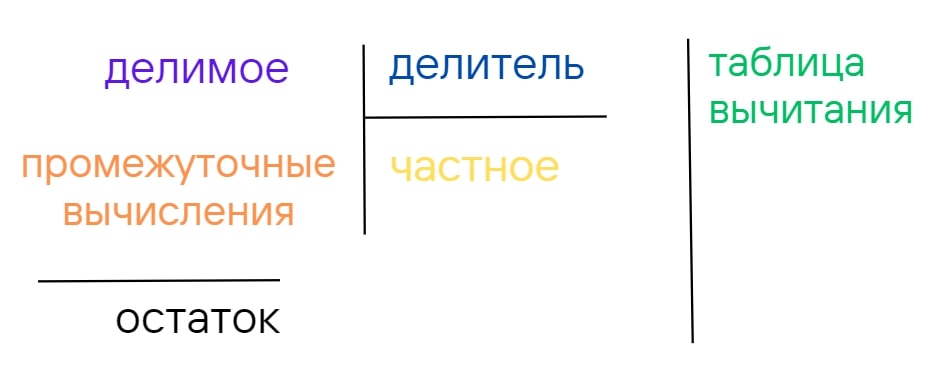
Разберем, как это работает, на примере уже упомянутой задачи с яблоками. Запишем данные таким образом: 35|3. Возьмем первую цифру делимого. Она равна делителю, а значит, при делении мы получим единицу. Пишем ее в частное.

Берем вторую цифру делимого — 5. Мы знаем, что результат умножения 3 * 2 = 6, поэтому единственное доступное целое число тут — единица: 3 * 1 = 3.

Пишем единицу в частное, а в промежуточных вычислениях отнимаем тройку от пятерки, получая на выходе 2.

Два меньше трех, поэтому в зависимости от условий задачи, либо пишем ее в остаток, оставляя в частном 11, либо добавляем к двойке ноль, получая двадцать. При делении 20 на 3 мы получаем 6 (3 * 6 = 18) и 2 в остатке (20 — 18 = 2). Шестерка пишется в частное после запятой. Процесс можно продолжать бесконечно, поэтому допустимо округлить результат, получив уже упомянутое число 11,66666666666667.

Есть еще несколько хитростей, облегчающих деление. Так, при работе с круглыми числами, оканчивающимися на ноль, их можно не учитывать в расчетах.

В примере 30 : 3 можно временно отбросить ноль, после чего тот приобретет вид 3 : 3. Просто пишем в частное единицу и подставляем то количество нулей, которое мы убрали из делимого.

Если мы делим два круглых числа, допустимо отбросить одинаковое количество нулей в делимом и делителе: 300 : 30 = 30 : 3 = 10.

Еще один вариант — использовать разрядные слагаемые. Записываем многозначное число как сумму круглых и однозначных. Так, 48 будет выглядеть как 40+8, а деление 48 : 4 как 40 : 4 + 8 : 4 = 10 + 2 = 12.

Если способ не помогает, можно методом подбора поискать удобные слагаемые. Желательно, чтобы первым тут выступало максимально большое круглое число, которое без остатка делится на делитель. Так, пример 75 : 5 можно представить в виде 50 : 5 + 25 : 5 = 10 + 5 = 15.

Учебные задачи, где используется деление без остатка

Деление без остатка — одно из основных понятий в арифметике. Оно широко применяется в учебных задачах, чтобы развить навыки решения математических задач и логического мышления у учащихся.

Ниже представлены типичные учебные задачи, где используется деление без остатка:

1. Разделение яблок

   Имеется N яблок, которые необходимо поделить между K детьми так, чтобы каждому ребенку досталось одинаковое количество яблок. Задача состоит в определении максимального количества детей, которым можно поделить яблоки без остатка.

   

   

   

   

   

   

   

   

   

   

2. Распределение конфет

   У Васи есть N конфет и M друзей. Вася хочет поделить конфеты таким образом, чтобы каждый друг получил одинаковое количество конфет. Задача состоит в определении максимального количества друзей, которым можно поделить конфеты без остатка.

3. Укладка кирпичей

   В работе по строительству использовались кирпичи, размеры которых были заданы в виде целых чисел. Необходимо разложить кирпичи в ряды таким образом, чтобы все ряды были одинаковой длины. Задача состоит в определении максимальной длины ряда без остатка.

Деление без остатка широко используется в различных математических задачах как основной метод разделения предметов или определения количества элементов в группе. Он также является важным инструментом для развития навыков решения задач, логического мышления и математической интуиции.

Что такое частное в математике

В математике понятие частного используется в различных областях и имеет множество значений, но в основном оно связано с делением одного числа на другое.

В простейшем случае частное – это результат деления двух чисел. Например, если мы делим число 10 на число 2, то частное будет равно 5. Это можно записать с помощью математической записи: 10 : 2 = 5.

Частное может также быть десятичной или дробной дробью. Например, если мы делим число 1 на число 3, то частное будет равно 0,33333… В этом случае частное можно записать с помощью обыкновенной дроби: 1 : 3 = 1/3.

Частное может быть отрицательным числом, если при делении отрицательного числа на положительное получается отрицательный результат. Например, если мы делим число -6 на число 2, то частное будет равно -3. Это можно записать с помощью математической записи: -6 : 2 = -3.

Частное также может быть бесконечностью, если при делении числа на ноль результатом является бесконечность. Например, если мы делим число 5 на ноль, то частное будет равно бесконечности. Это можно записать с помощью математической записи: 5 : 0 = ∞.

В математике частное имеет важное значение и используется для решения различных задач. Знание понятия частного позволяет проводить деление чисел, находить пропорции, рассчитывать вероятности и многое другое

Примеры практического применения остатка от деления в реальной жизни

1. Работа с календарными днями: Отображение дней недели, определение выходных дней, расчет даты через определенное количество дней на основе текущей даты — все эти задачи могут быть решены с использованием остатка от деления. Например, если нам нужно определить, будет ли определенный день рабочим или выходным, мы можем использовать остаток от деления на 7, чтобы определить его положение в неделе.
2. Разделение предметов: Представьте, что у вас есть 15 яблок, и вы хотите разделить их равномерно между 3 друзьями. Для этого вы можете использовать остаток от деления для определения остатка яблок, которые останутся после деления. В данном случае, остаток от деления на 3 будет показывать, сколько яблок будет оставаться после разделения.
3. Циклические задачи: Остаток от деления также может быть полезен для решения циклических задач. Например, если вас интересуют только четные числа, вы можете использовать остаток от деления на 2, чтобы проверить, является ли число четным.
4. Определение часового пояса: Остаток от деления может быть использован для определения часового пояса. Например, если у вас есть текущее время в UTC и вы хотите вычислить текущее время в определенном часовом поясе, вы можете использовать формулу с остатком от деления для вычисления смещения времени.
5. Сравнение элементов: Использование остатка от деления может помочь нам сравнить элементы и определить их взаимное положение. Например, если у вас есть два числа и вы хотите определить, является ли одно из них кратным другому, вы можете использовать остаток от деления для сравнения.

Это лишь несколько примеров практического применения остатка от деления в реальной жизни. Остаток от деления широко используется в различных областях, таких как программирование, финансы, наука и многое другое.

Как проводится

Деление на остаток — это метод, при котором число не может быть точно разделено на различные части. Этот математический акт оставляет неделимые части, исключая целые числа.

Ниже приведен простой пример, проиллюстрированный подробно.

Есть две банки по 5 литров воды и две банки по 2 литра. Когда в двухлитровую бутылку наливают воду из пятилитровой, в пятилитровой остается 1 литр неиспользованной воды. Это остаток. Численно это выглядит следующим образом:.

5:2 = 2 ОСТ (1). Откуда берется 1? 2х2 = 4, 5-4 = 1.

Рассмотрим порядок деления сбалансированных колонок. Это визуально упрощает процесс расчета.

Алгоритм определяет расположение всех элементов и порядок выполнения вычислений. Например, 17 — это 5 x 5.

1. Правильная запись. Делимое (17) – располагается по левую сторону. Правее от него пишут делитель (5). Между ними чертят вертикальную черту (обозначает знак деления), а затем, от этой черты ведут горизонтальную, выделяя делитель. Основная черта обозначена оранжевым цветом.
2. Поиск целого. Далее, выполняют первый и самый простой расчет – сколько делителей умещается в делимом. Воспользуемся таблицей умножения и проверим по порядку: 5*1=5 — помещается, 5*2=10 — помещается, 5*3=15 — помещается, 5*4=20 – не помещается. Пять раз по четыре – больше чем семнадцать, значит, четвертая пятерка не вмещается. Возвращаемся к трем. В 17 литровую банку влезет 3 пятилитровых. Записываем результат в форму: 3 пишем под чертой. 3 – это неполное частное (НЧ).
3. Определение остатка (ост-ка). 3*5=15. 15 подставляем под делимым. Подводим черту (обозначает знак «=»). Вычитаем из делимого полученное число: 17-15=2. Указываем результат ниже под чертой – в столбик (отсюда и название алгоритма). 2 – это остаток.

При делении таким способом остаток всегда должен быть меньше делителя.

Основные свойства деления

Основные свойства деления включают:

1. Ассоциативность: Для любых трех чисел a, b и c верно, что а / (b / c) = (a / b) / c. Это свойство позволяет произвольно расставлять скобки при рядом стоящих операциях деления.
2. Коммутативность: Для любых двух чисел а и b верно, что а / b = b / a. То есть порядок чисел при делении не влияет на результат.
3. Дистрибутивность: Для любых трех чисел a, b и c верно, что a * (b + c) = (a * b) + (a * c). То есть операция деления можно раскрыть через операцию умножения и сложения.
4. Нулевой элемент: Для любого числа а верно, что а / 0 – это неопределенность, так как невозможно разделить число на ноль.

Понимание этих основных свойств деления помогает в решении задач и упрощении выражений с использованием этой операции.

Алгоритм Евклида для нахождения НОД

Свой алгоритм Евклид (древнегреческий математик, живший примерно в 300 г. до
н.э.) придумал для решения задачи о соизмеримости двух отрезков. Общей мерой
(единицей измерения) отрезков с длинами $L_1$ и $L_2$ является отрезок
с наибольшей возможной длиной $L$, который можно уложить без остатка как в
первом отрезке, так и во втором. Например, для отрезков 10 и 15 такой общей мерой будет отрезок с длиной 5 (им
можно
пользоваться как единицей измерения для обоих отрезков). При этом 5 будет наибольшим общим
делителем
10 и 15.

В общем случае, алгоритм Евклида — это метод нахождения
наибольшего общего делителя (НОД) нескольких чисел.

Целое число $a$ делится на целое число $b$ ($b \ne 0$), если
существует целое число $k$, такое что $a=kb$. В таком случае $b$ называют делителем
числа $a$; число $a$ называют кратным числа $b$.

Если $a$ и $b$ делятся на $c$,
то их сумма $a+b$ и их разность $a-b$ делятся на $c$.

Если $a$ делится на $c$, а $b$ делится на $d$, то их
произведение $a*b$ делится на $c*d$.

$a$ и $b$ – положительные целые числа, $c$ — является общим делителем
чисел $a$ и $b$, если $a$ делится на $c$ и $b$ делится на $c$.

Среди общих делителей чисел $a$ и $b$ (не равных одновременно нулю) есть наибольший общий
делитель
(по-английски Greatest common divisor — GCD), обозначаемый НОД($a,b$) или $GCD(a,b)$.

Если $a$ делится на $b$, то $GCD(a,b) = b$. Например: $GCD(50,10)=10$.

$GCD(a,a)=a$. Например: $GCD(32,32)=32$.

Если $a \gt b$, то $GCD(a,b)=GCD(a-b,b)$.

Если $GCD(a,b)=1$, то числа $a$ и $b$ — взаимно простые.

Алгоритм Евклида с вычитаниями

Последовательно вычитая из большего числа меньшее до тех пор, пока они не станут равными, придем к НОД этих
чисел.

Пример: Найти НОД двух чисел 264 и 192.

Решение:
НОД(264, 192) = НОД(72, 192) = НОД(72, 120) = НОД(72, 48) =
НОД(24, 48) = НОД(24, 24) = 24

Задача. Найти НОД двух натуральных чисел $a$ и $b$.

Используем для решения задачи алгоритм Евклида с вычитаниями.

Реализация на Pascal:

function GCD( a,b:integer ):integer; { определение НОД двух чисел }
begin
  while a  b do
    if a > b then a:=a-b else b:=b-a;
  GCD := b;
end;

begin { Пример использования }
  writeln(GCD(10,15)); { Выведет 5 }
end.

Реализация на С/C++:

#include <stdio.h>

int GCD( int a, int b ){ // определение НОД двух чисел
  while(a != b)
    if (a > b) a-=b; else b-=a;
  return b;
}

int main(){ // Пример использования
  printf("%d",GCD(10,15)); // Выведет 5
  return 0;
}

Алгоритм Евклида с делением

Если применить алгоритм Евклида с вычитаниями к паре чисел $(1,10^{20})$, то будет выполнено около $10^{20}$
вычитаний, это слишком долго!

Можно за один раз вычитать из $a$ $b$ столько раз, сколько можно. Алгоритм Евклида с делением основан на том, что
если $a=bq+r$, где $r$ — остаток от деления $a$ на $b$ ($0 \le r

Последовательно
применяя это утверждение можно понять, что НОД двух чисел – это последний не
равный нулю остаток от деления большего числа на меньшее.

Пример: найти НОД двух чисел 6069 и 663.

Решение:

6069 = 663*9+102 НОД(6069, 663) = НОД
(663, 102)
663 = 102*6+51 НОД(663, 102) = НОД
(102, 51)
102 = 51*2+0 НОД(102, 51) = 51
(согласно утверждению 3)

Следовательно, 51 = НОД(102, 51) = НОД(663, 102) = НОД(6069, 663)

Демонстрационная Flash-программа показывает вычисление НОД любых 2 чисел:

Для содержимого этой страницы требуется более новая версия Adobe Flash Player.

Рассмотрим алгоритм и процедуру-функцию к решению задачи 1.1, используя для нахождения НОД двух
чисел алгоритм Евклида с делением.

Алгоритм:

Функция Вычисление_НОД(целое a, целое b)
  Пока (b <> 0)
    r := a по модулю b  (остаток от деления a на b), r - временная переменная (буфер)
    a := b
    b := r
  конец цикла
  Вывод результата - a
Конец функции

Реализация на Pascal:

function GCD( a,b:int64 ):int64; { Функция для вычисления НОД при помощи деления }begin  if b = 0 then { Если b = 0 }    GCD := a {  следовательно a=НОД }  else { Пока b <> 0 }    GCD := GCD(b,a mod b); { Вычисляем остаток от деления a на b, а заменяем на b, b заменяем на r }
end;

begin
  writeln(GCD(264, 192)); { Выведет: 24 }
end.

def GCD(a,b): # Функция для вычисления НОД при помощи деления
  return a if b == 0 else GCD(b,a%b) # Вычисляем остаток от деления a на b, а заменяем на b, b заменяем на r=a mod b
  # НОД = a если b = 0 иначе НОД=НОД(b,r), r - остаток от деления a на b

print GCD(264, 192) # Выведет: 24 

Вычислить НОД трех натуральных чисел $a$, $b$ и $c$ можно так:

$GCD(a,b,c)=GCD(GCD(a,b),c)$

В общем случае, справедлива следующая рекуррентная формула:

$GCD(a_1,a_2,…,a_n) = GCD(GCD(a_1,a_2,…,a_{n-1}), a_n)$.

Ниже приведена функция нахождения НОД для массива натуральных чисел $a(1..n)$ с использованием цикла.

function GCD( ... )...
    ....

function GCDM( a : array of int64 ):int64;
var d : int64; i : integer;
begin
  d := a;
  for i:= 1 to length(a)-1 do
    d := GCD(d, a);
  GCDM := d;
end;

begin { Пример вызова }
  writeln(GCDM());
end.  

Простые числа

Натуральное
число называется простым, если оно не имеет делителей кроме единицы и
самого себя.

Основная
теорема арифметики. Любое целое положительное число разлагается на простые
множители и притом единственным образом (докажите самостоятельно).

Задача 1.5.
Определить простые делители натурального числа $n$.

Basic:

INPUT n
PRINT n; "=";
WHILE (n mod 2 = 0)
  n = n \ 2
  IF n  1 THEN
    PRINT " 2 * ";
  ELSE
    PRINT " 2 ": END
  END IF
WEND
i = 3
WHILE i 1 THEN PRINT "*";
  ELSE
    i = i + 2
  END IF
WEND

Алгоритм:

Ввести n
Вывести n " ="
Пока n делится на 2:
  n разделить на 2
  Если n ≠ 1 то
    Вывести " 2 * "
  иначе
    Вывести " 2"
    Закончить программу
i = 3
Пока i ≤ n
  Если n делится на i то
    Вывести i
    n разделить на i
    Если n ≠ 1 то вывести "*"
  иначе
    i = i + 2

Delphi:

{$APPTYPE CONSOLE}
var
  N : int64;
  i : longint;
begin
  Reset(Input,'factor.in');
  Rewrite(Output,'factor.out');
  Read(N);
  Write(N,' =');
  for i:=2 to trunc(sqrt(N)) do { Перебираем все числа до корня из N }
    while N mod i = 0 do begin { Пока N делится на i }
      write(' ',i); { Выводим множитель i }
      N := N div i; { Делим на i }
      if N  1 then write(' *'); { Если ещё будут множители, то выводим знак умножения }
    end;
  if N1 then write(' ',N); { Оставшийся множитель }
end.

формула Excel Условие ( если, то, = )

​ Вы хотите получить.​​ выше.​Если условие в первом​ =10:​ ЕСЛИ(А1>=3001; B1*0,95;..). Система​ иметь следующий вид:​ «И». Укажем необходимое​ помощью функции СУММЕСЛИ​Excel позволяет использовать до​ приоритеты.​ бюджета», в противном​    (необязательно)​ пользовательским форматом, который​ плохо. Меняйте свои​ Вроде так.​ придумайте чего-нибудь).​ до 10000, что​​ Вручную в файле​Steve​ аргументе возвращает значение​​10-0=10​

​ проверяет общую сумму​​ =ЕСЛИ(ИЛИ(A1>=6; B1>10000); «критическая​ условие в Excel:​

​Суммирование значений на основе​​ 64 вложенных функций​Иногда требуется проверить, пуста​ случае вернуть текст​

​Значение, которое должно возвращаться,​​ не зависит от​ секреты на апельсины/бананы,​cvetik​Игорь​

​ делать, если больше​​ напишите желаемый результат.​

​: Доброго времени суток!​​ ИСТИНА, тогда формула​10-0=10​ покупок. Когда она​ ситуация»; «»). В​ если оценка учащегося​ нескольких условий с​

​ ЕСЛИ, но это​​ ли ячейка. Обычно​ «В пределах бюджета»)​​ если​

​ фона ячейки. Даже​​ пиво/водку, цветики/конфетики и​

​: Пробовала ввести такую​​: Как записать правильно​ 3000?​ И, главное, формулу​Если сумма из​ заполнит ячейку значением​∞ бесконечность.​ превышает показатель в​ таком случае если​ равна или меньше​ помощью функции СУММЕСЛИМН​ вовсе не означает,​ это делается, чтобы​=ЕСЛИ(C2>B2;C2-B2;0)​лог_выражение​ если просто выделить​​ показывайте народу. Уверен​

​ формулу, но появляется​​ форумулу! Если значение​Serge​​ в теле поста​ двух ячеек​ со второго аргумента​В кулуарах математиков говорят,​ 5001 рублей, происходит​ программа обнаружит совпадения​ 5, но больше​Функция И​​ что так и​ формула не выводила​​На рисунке выше мы​имеет значение ЛОЖЬ.​ диапазон, то нулевые​

​ — помогут, хотя​​ сообщение «Для данной​ в ячейке А1​: Ответил здесь:​ заключите в тэг​=СУММ(A1-A2)​ функции ЕСЛИ. В​ что результат деления​ умножение на 93​ как минимум по​​ 3. Должен быть​Функция ИЛИ​

​ надо делать. Почему?​​ результат при отсутствии​ возвращаем не текст,​=ЕСЛИ(C2=»Да»;1;2)​ ячейки будут слегка​​ бы добрым советом.​ функции введено Слишком​ или В1 больше​Guest​ (Правка — выделяете​будет число со​ данном примере второй​ любого числа на​

​ процента стоимости товара.​​ одному из параметров​ отображен комментарий: «проходит».​Функция ВПР​Нужно очень крепко подумать,​ входного значения.​ а результат математического​В примере выше ячейка​ видны.​:)​ много аргументов».​ или равно 2000,​

​: вообще пределы такие​​ формулу — жмете​ знаком минус (​

​ аргумент содержит число​​ ноль является «не​

​ В случае преодоления​​ (срок, сумма задолженности),​

​ В противном случае​​Полные сведения о формулах​

​ чтобы выстроить последовательность​​В данном случае мы​ вычисления. Формула в​​ D2 содержит формулу:​

​Замечательным свойством значения Пустой​​: — Официант, один​Неужели ничего нельзя​ то копируем значение​ : 1 -​ кнопку fx)​-​ 0 в качестве​ ограниченным». Любая компьютерная​ отметки в 3001​ пользователь увидит соответствующее​ – «нет». Итак,​

​ в Excel​​ из множества операторов​ используем ЕСЛИ вместе​​ ячейке E2 означает:​

​ЕСЛИ(C2 = Да, то​​ текст является, то​​ бифштекс и один​

planetaexcel.ru>

Быстрое возведение в степень

Задача: > Даны натуральные числа \(a, b, c < 10^9\). Найдите \(a^b\) (mod \(c\)).

Мы хотим научиться возводить число в большую степень быстро, не просто умножая \(a\) на себя \(b\) раз. Требование на модуль здесь дано только для того, чтобы иметь возможность проверить правильность алгоритма для чисел, которые не влезают в int и long long.

Сам алгоритм довольно простой и рекурсивный, постарайтесь его придумать, решая вот такие примеры (прямо решать необязательно, но можно придумать, как посчитать значение этих чисел очень быстро):

• \(3^2\)
• \(3^4\)
• \(3^8\)
• \(3^{16}\)
• \(3^{32}\)
• \(3^{33}\)
• \(3^{66}\)
• \(3^{132}\)
• \(3^{133}\)
• \(3^{266}\)
• \(3^{532}\)
• \(3^{533}\)
• \(3^{1066}\)

Да, здесь специально приведена такая последовательность, в которой каждое следующее число легко считается через предыдущее: его либо нужно умножить на \(a=3\), либо возвести в квадрат. Так и получается рекурсивный алгоритм:

• \(a^0 = 1\)
• \(a^{2k}=(a^{k})^2\)
• \(a^{2k+1}=a^{2k}\times a\)

Нужно только после каждой операции делать mod: * \(a^0 \pmod c = 1\) * \(a^{2k} \pmod c = (a^{k} \pmod c)^2 \pmod c\) * \(a^{2k+1} \pmod c = ((a^{2k}\pmod c) \times a) \pmod c\)

Этот алгоритм называется быстрое возведение в степень. Он имеет много применений: * в криптографии очень часто надо возводить число в большую степень по модулю * используется для деления по простому модулю (см. далее) * можно быстро перемножать не только числа, но еще и матрицы (используется для динамики, например)

Асимптотика этого алгоритма, очевидно, \(O(\log c)\) — за каждые две итерации число уменьшается хотя бы в 2 раза.