Вопрос-ответ:
Почему математика считается основой науки?
Математика является основой науки из-за ее системных и логических подходов, которые позволяют абстрагировать реальные явления и описывать их в виде формул и уравнений. Это позволяет разрабатывать более точные и точные модели, которые затем могут быть использованы для предсказания различных явлений.
Как математика используется в технологиях?
Математика используется в технологиях для создания различных алгоритмов и способов оптимизации производственных процессов. К примеру, математические алгоритмы используются для оптимизации сетей машинного обучения, что позволяет ускорять обучение и получать более точные результаты.
Какие математические концепции используются в экономике?
В экономике используются многие математические концепции, такие как геометрия, теория вероятности, анализ функций, дифференциальные уравнения и т.д. Они используются для моделирования различных явлений, например, для определения оптимальных цен на товары, прогнозирования спроса и т.д.
Как математика связана с развитием компьютерных игр?
Математика используется в разработке компьютерных игр для создания реалистичной физики, графики и искусственного интеллекта. Также математические алгоритмы используются для создания карт и генерации мира, что позволяет игрокам иметь различные варианты переживания игрового процесса.
Как математика помогает в изучении климата и географии?
Математика используется в изучении климата и географии для моделирования и прогнозирования различных явлений, как например, изменение климата, изменение уровня воды, сейсмические активности и т.д. Также математические модели позволяют улучшить метеорологическую и гидрологическую прогнозную системы.
Какие свойства математических объектов могут иметь практическое применение?
Математические объекты, такие как графы, матрицы, дифференциальные уравнения и т.д., имеют множество свойств, которые могут быть использованы для решения различных практических задач. Например, свойства графов используются в моделировании транспортных и коммуникационных сетей, а свойства матриц используются в теории решения линейных уравнений и обработке данных.
Что такое теория игр в математике?
Теория игр — это раздел математики, который занимается исследованием стратегий и принятия решений в конфликтных ситуациях. Она может быть применена в различных областях, таких как экономика, политика, бизнес и т.д. Теория игр позволяет разрабатывать математические модели конфликтных ситуаций и определять оптимальные стратегии для каждого участника игры.
Как математика может помочь в повседневной жизни?
Математика может помочь в повседневной жизни в различных сферах, например, при расчете бюджета, выборе инвестиций, создании графиков и диаграмм, что позволяет более точно понимать различные явления и принимать взвешенные решения. Также математика помогает развивать стратегическое мышление и логику.
Какие понятия используются в геометрии?
В геометрии используются различные понятия, которые позволяют описывать и изучать геометрические фигуры и их свойства.
- Точка — это базовое понятие геометрии. Точка не имеет размеров и обозначается заглавной латинской буквой.
- Прямая — это бесконечное множество точек, которые лежат на одной линии. Прямую обозначают двумя точками или маленькой латинской буквой.
- Отрезок — это конечное множество точек на прямой, соединенных двумя конечными точками. Отрезок обозначается двумя точками над ним.
- Угол — это область между двумя лучами, имеющими общее начало. Угол измеряется в градусах (°) или радианах (рад).
- Треугольник — это фигура, образованная тремя отрезками, которые называются сторонами треугольника. Треугольник может быть разносторонним, равнобедренным или равносторонним.
- Полигон — это фигура, образованная отрезками, которые называются сторонами полигона. Полигон может быть треугольником, четырехугольником или многоугольником.
- Фигура — это геометрическое образование, которое имеет площадь и периметр. Фигуры могут быть плоскими или пространственными.
Это лишь некоторые из понятий, используемых в геометрии. Геометрия имеет много различных концепций и терминов, которые помогают понять и изучать геометрические объекты и их взаимодействие.
Вариант 2
Когда я думаю о математике, передо мной встают картины загадочных чисел, формул и головоломок. Но постепенно я начинаю осознавать, что математика – это не только сложные задачи на уроках, но и неотъемлемая часть моей повседневной жизни. В этом сочинении я расскажу о том, как математика влияет на мою жизнь и почему она так важна для меня.
Математика окружает меня повсюду. Она помогает мне разобраться во времени, чтобы я мог точно планировать свои дела и не опаздывать. Когда я играю в настольные игры, математика помогает мне считать очки, делать правильные ходы и выявлять лучшие стратегии. Даже когда я решаю простые задачи на кухне, математика приходит на помощь – я мерю ингредиенты, вычисляю пропорции, чтобы получить вкусный результат.
Более того, математика помогает мне развивать свой ум. Когда я решаю задачи и головоломки, я тренирую свою логику, умение анализировать и находить пути решения. Это умение пригодится мне не только в школе, но и в будущей жизни. Ведь когда я стану взрослым, мне предстоит принимать важные решения, и математика научит меня рассчитывать все возможные варианты и выбирать оптимальное решение.
Однажды у меня была возможность помочь родителям вести бюджет. Я помогал(а) составлять список расходов и доходов, считал(а) суммы, делал(а) простые расчеты
Благодаря этому опыту я понял(а), как важно уметь работать с числами, чтобы не тратить больше, чем есть, и быть финансово ответственным
Математика – это нечто большее, чем просто школьный предмет. Она является неотъемлемой частью нашей повседневной жизни. Она помогает мне разобраться во времени, играть с друзьями, готовить вкусные блюда и даже помогает вести учет финансов. Благодаря математике я развиваю свой ум, учусь логическому мышлению и нахожу радость в решении головоломок. Я уверен(а), что математика играет важную роль в моей жизни, и я буду стараться изучать ее с интересом и усердием, чтобы развивать свои способности и быть готовым(ой) к сложностям, которые ждут меня в будущем. Математика – это ключ к пониманию мира вокруг нас, и я рад(а), что она является неотъемлемой частью моей жизни.
Мне нравится1.7 k.Не нравится837
Алгебра и геометрия — неотъемлемая часть повседневной жизни
Алгебра и геометрия, хотя и кажутся сложными и абстрактными на первый взгляд, фактически играют важную роль в нашей повседневной жизни. Эти математические дисциплины помогают нам развивать логическое мышление, решать проблемы, прогнозировать результаты и принимать взвешенные решения.
Алгебра используется во многих сферах жизни, таких как финансы, инженерия, архитектура и компьютерные науки. Знание алгебры позволяет нам анализировать данные, строить и интерпретировать графики, решать уравнения и неравенства. Такие навыки особенно полезны при планировании бюджета, инвестировании и расчетах во многих других ситуациях.
Геометрия, в свою очередь, помогает нам понять и визуализировать пространственные отношения. Она используется в архитектуре, дизайне, строительстве, навигации и даже в нашей ориентации в пространстве. Знание геометрии позволяет нам планировать и строить дома, прокладывать дороги, создавать красивые и эргономичные предметы, а также понимать мир вокруг нас.
Без знания алгебры и геометрии мы бы не смогли развивать технологии и научные открытия, которые существенно улучшают качество нашей жизни. Такие важные области, как компьютерное моделирование, медицина и физика, тесно связаны с этими математическими дисциплинами. Поэтому не удивительно, что алгебра и геометрия являются неотъемлемой частью образования и постоянно применяются в повседневной жизни.
В конечном итоге, знание алгебры и геометрии помогает нам стать более компетентными и уверенными в себе в решении различных задач и проблем. Каким бы сферам жизни мы ни занимались, математические навыки всегда будут полезны и ценными.
Смежные углы и их свойства
Смежные углы — соседи, живущие через стенку.
Из свойств лучей нам известно, что вкупе образуют прямую. Таким образом, смежные углы — углы-соседи, «проживающие» на одной прямой. Эта геометрическая особенность подразумевает ряд интересных свойств, одно из которых — связь смежных с развернутыми углами.
Градусная мера смежных углов
Доказательство
Пусть $\angle{ABD}$ и $\angle{DBC}$ — произвольные смежные углы. Докажем, что сумма смежных углов равняется $180^\circ$. Заметим, что луч $BD$ проходит между сторонами развернутого угла $\angle{ABC}$. Градусная мера развернутого угла равняется $180^\circ$.
По $A_8$ мы помним, что градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. Значит:
$$\angle{ABC}=\angle{ABD}+\angle{DBC}=180^\circ$$
Градусная мера смежных углов в сумме составляет $180^\circ$. Что и требовалось доказать.
Задача. Какова градусная мера смежных углов, если про смежные углы известно, что один их них в три раза больше другого?
Решение. Обозначим градусную меру меньшего угла как $x$. Если больший угол больше меньшего в три раза, его градусную меру можно обозначить как $3x$. Сумма смежных углов составляет $180^\circ$. Пользуясь данным свойством, составим следующее уравнение:
$$x+3x=180^\circ$$
Откуда получаем значение меньшего угла $x=45^\circ$. Больший угол по условию больше в три раза и, следовательно, будет равняться $135^\circ$. Градусная мера смежных углов найдена и составляет $45^\circ$ и $135^\circ$.
Ответ: $45^\circ$, $135^\circ$.
{"questions":[{"content":"`speech-1`Разность двух смежных углов равна $40^\\circ$. Найдите градусные меры данных углов. Впишите значения ниже в любом порядке. `input-6``input-16`","widgets":{"speech-1":{"type":"speech","text":"Ваша очередь попробовать посчитать!"},"input-6":{"type":"input","unit":"$^\\circ$","answer":},"input-16":{"type":"input","unit":"$^\\circ$","answer":}},"step":1,"hints":}]}
Сумма смежных углов: следствие из теоремы
Поскольку градусная мера смежных углов в сумме строго определяется как $180^\circ$, это позволяет сделать вывод о том, что если два угла равны, то равны будут и смежные с ними углы. В геометрии бездоказательно выводы приводить нельзя, так что оформим данное наблюдение в виде следствия из теоремы и докажем его.
Итак:
Доказательство
Рассмотрим два равных угла — $\angle{1}$ и $\angle{2}$. Если углы равны, равны их градусные меры. Обозначим градусную меру углов как $x$ и запишем следующее:
$$\begin{cases}\angle{1}=x^\circ\\\angle{2}=x^\circ\end{cases}$$
Сумма смежных углов равняется $180^\circ$. Тогда смежный угол с $\angle{1}$ равен «$180^\circ-x^\circ$». То же самое заключаем про градусную меру угла, смежного с $\angle{2}$: «$180^\circ-x^\circ$». У равных углов $\angle{1}$ и $\angle{2}$ равные смежные углы. Что и требовалось доказать.
{"questions":[{"content":"Градусная мера $\\angle{\\alpha}$, смежного с $\\angle{\\gamma}$, составляет $55^\\circ$. Чему равняется $\\angle{\\beta}$, если известно, что угол, смежный с $\\angle{\\beta}$, по градусной мере равен $\\angle{\\alpha}$? `input-1`","widgets":{"input-1":{"type":"input","unit":"$^\\circ$","answer":"125"}},"step":1,"hints":["Чтобы не запутаться, определим количество углов, задействованных в задаче. У нас имеется $\\angle{\\alpha}$, $\\angle{\\gamma}$, $\\angle{\\beta}$ и угол, смежный с $\\angle{\\beta}$. Для простоты обозначим его как $\\angle{\\phi}$.","По условию известно, что $\\angle{\\gamma}$ и $\\angle{\\alpha}$ — смежные углы. Также смежными являются $\\angle{\\beta}$ и $\\angle{\\phi}$.","По следствию из теоремы о сумме смежных углов мы знаем, что у равных углов равны смежные с ними углы.","Если $\\angle{\\phi}=\\angle{\\alpha}=55^\\circ$, то $\\angle{\\gamma}=\\angle{\\beta}=180^\\circ-55^\\circ=125^\\circ$.","Ответ: $125^\\circ$."]}]}
Вариант 5
Когда я думаю о математике, передо мной встает мир загадок и открытий. Математика – это язык, на котором говорит сама природа, и инструмент, который помогает мне понимать и изучать мир вокруг нас
В этом сочинении я расскажу о том, как математика влияет на мою жизнь и почему я считаю ее важной
Математика – это больше, чем просто учебный предмет. Она помогает мне развивать умение мыслить логически, решать задачи и анализировать информацию. Когда я изучаю математику, я учусь находить закономерности, рассуждать систематически и находить точные ответы. Например, когда я решаю задачу про расстановку книг на полке, я использую знания математики о порядке и пространстве.
Математика также помогает мне в повседневной жизни. Когда я покупаю сладости в магазине, математика помогает мне рассчитать стоимость товара и проверить, хватает ли у меня денег. Когда я готовлю семейный ужин, я использую математику для измерения ингредиентов и регулирования времени приготовления. Математика также помогает мне понимать финансовые вопросы, такие как бюджетирование и сбережения.
Математика – это важный инструмент, который помогает мне понимать мир и развивать мои навыки мышления. Она применима не только в школе, но и в повседневной жизни. Знания математики помогают мне решать проблемы, анализировать информацию и принимать обоснованные решения. Поэтому я учу математику с интересом и увлечением, и считаю, что она будет полезной для меня в будущем.
Когда я слышу слово «математика», у меня в голове сразу возникает ощущение загадки, интереса и возможностей.
Математика – это язык, на котором говорит сам мир. Она пронизывает все сферы моей жизни и помогает мне понимать и анализировать окружающую действительность
В этом сочинении я расскажу о том, как математика влияет на мою жизнь и почему я считаю ее невероятно важной
Математика – это больше, чем просто школьный предмет. Она является фундаментом для многих других наук и дисциплин, а также применима в повседневной жизни. Когда я изучаю математику, я развиваю свои навыки абстрактного и логического мышления, а также способность решать сложные задачи. Например, при изучении геометрии я научился определять формы и размеры объектов, что помогает мне разбираться в архитектуре, дизайне и строительстве.
Математика также играет важную роль в повседневных ситуациях. Когда я делаю покупки, я использую математические навыки для расчета стоимости товаров, скидок и сдачи. Когда я планирую свое время, математика помогает мне оценить продолжительность задач и распределить время эффективно. Например, если у меня есть несколько заданий и ограниченное время, я могу использовать математические навыки, чтобы определить, сколько времени мне нужно на каждую задачу и как распределить свое время равномерно.
Математика – это неотъемлемая часть моей жизни, которая помогает мне развивать логическое мышление, принимать обоснованные решения и понимать мир вокруг меня. Она применима в различных сферах – от науки и технологий до повседневных ситуаций. Благодаря математике я становлюсь увереннее в себе и готов к сложностям, с которыми я сталкиваюсь. Поэтому я с радостью изучаю математику и понимаю, что она играет важную роль в моей жизни и открывает передо мной множество возможностей.
Мне нравится680Не нравится398
Свойства углов
Рассмотрим свойства углов треугольника:
- против большей стороны лежит больший угол, а также наоборот — против большого угла лежит большая сторона;
- напротив равных сторон располагаются равные углы, а также наоборот — напротив равных углов находятся равные стороны (даже если все углы в равностороннем треугольнике равны);
- сумма углов треугольника равняется 180° (таким образом, каждый угол в равностороннем треугольнике равняется 60°);
- если продолжить одну из сторон треугольника, получится внешний угол;
- любая сторона треугольника будет меньше суммы двух иных сторон, а также больше их разности:a < b+c; a > b−c; b < a+c; b > a−c; c < a+b; c > a−b;
- если две параллельные прямые пересекаются секущей, то соответствующие углы равны;
- две плоскости можно назвать перпендикулярными, если двугранный угол между ними равняется 90°.
Зачем находить разность углов?
Разность углов — это математическая операция, которая позволяет определить разницу между двумя углами. Это может быть полезно в различных ситуациях, как в повседневной жизни, так и в различных научных и технических областях.
В повседневной жизни
- Определение направления: нахождение разности углов может помочь нам определить направления движения, навигацию и ориентирование в пространстве. Например, при использовании компаса или навигационной системы.
- Азимут: разность углов используется для определения азимута (угла между направлением на север и расположением объекта) в навигации и геодезии.
В научных и технических областях
- Geometric sequencing and measuring angles: нахождение разности углов является важным шагом при измерении и анализе углов в геометрии и тригонометрии.
- Control systems and robotics: разность углов может использоваться в системах управления и робототехнике для определения отклонения от заданного направления или позиции.
- Image processing and computer vision: в компьютерном зрении и обработке изображений нахождение разности углов может быть полезным при определении поворота или ориентации объектов на изображении.
В общем, нахождение разности углов является важным математическим инструментом, который находит применение в различных областях науки, техники и повседневной жизни.
Равенство смежных углов
Смежные углы — это два угла, имеющих общую сторону и вершину. Например, углы АВС и СВD на рисунке являются смежными углами.
Смежные углы могут быть как остроугольными, так и тупоугольными. Главное условие, чтобы у них была общая сторона и вершина. Смежные углы могут взаимодействовать друг с другом и с другими углами. Равенство смежных углов — это когда два смежных угла имеют одинаковую меру. То есть, если угол АВС и угол СВД равны, то они являются равными смежными углами.
Равенство смежных углов имеет важное значение в геометрии. Это условие является также одним из базовых для теоремы о параллельных линиях
Если две прямые пересекаются, то все вертикальные углы на этих прямых равны между собой. В свою очередь, равенство вертикальных углов равносильно равенству смежных углов, если эти углы находятся на параллельных прямых.
Для геометрических вычислений и построения геометрических фигур, равенство смежных углов помогает определить внутренние и внешние углы многоугольников, углы треугольников, параллельность прямых и многое другое. Поэтому, знание равенства смежных углов является необходимым для успешного изучения геометрии.
| Пример | Равенство смежных углов |
|---|---|
|
Угол ACD = углу CDF. Оба угла являются смежными углами, так как они имеют общую сторону и вершину. Их равенство говорит о том, что углы ACD и CDF равны между собой. |
Общие сведения
Основными элементами, используемыми в геометрии, являются лучи и углы. С их помощью образуется любая геометрическая фигура — квадрат, треугольник или любого вида многоугольник. Луч — это полупрямая, то есть часть линии, на которой точки располагаются по одной стороне от зафиксированной. По-другому можно сказать, что луч — это линия, ограниченная только с одной стороны. Обозначают его как прописными латинскими буквами, так и заглавными с названием точек. Во втором случае первой указывается начальная точка.
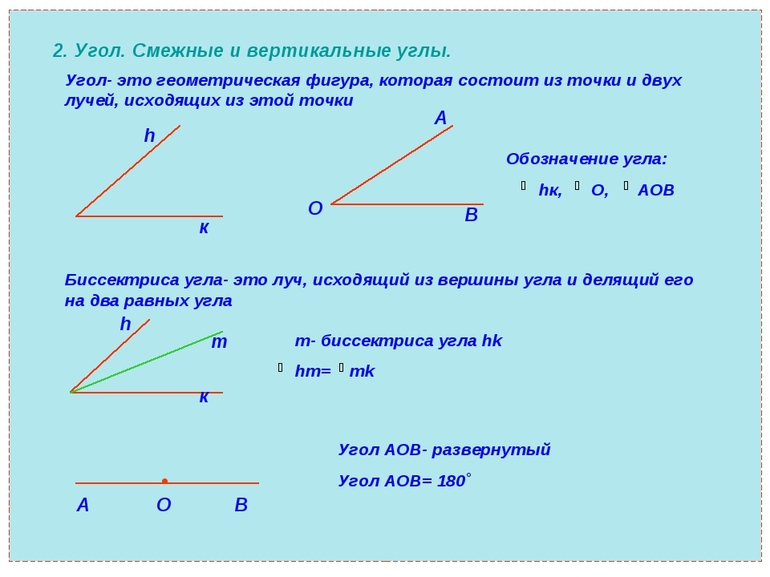
Два луча, выходящие из одной точки, образовывают угол. По сути, это незамкнутая геометрическая фигура. Она имеет вершину (общую точку) и стороны. Обозначают его с помощью трёх заглавных букв, соответствующих трём точкам — вершине и двум лежащим на разных сторонах лучах. Внутренняя часть формируется из множества точек, принадлежащих плоскости, ограниченной сторонами угла.
Существует шесть видов углов:
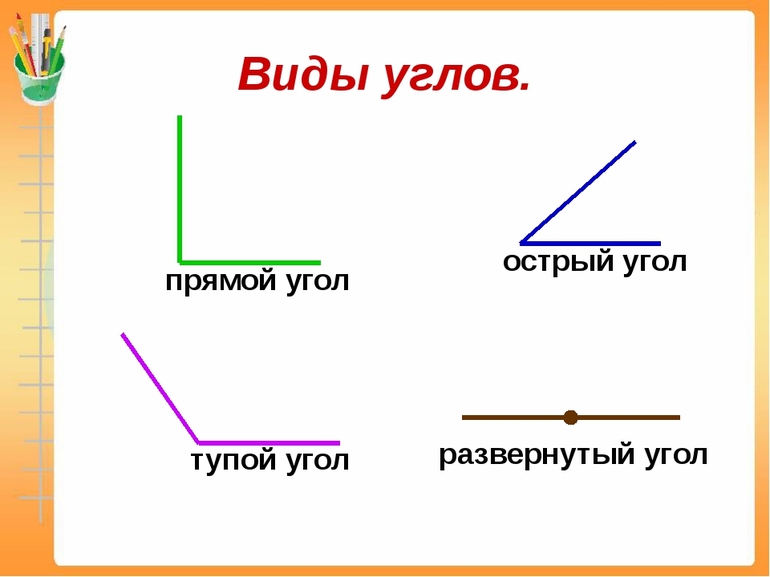
- Острый — расстояние между сторонами составляет меньше 90 градусов.
- Прямой — образовывается двумя взаимно перпендикулярными прямыми.
- Тупой — разворот угла больше 90 градусов, но не превышает 180.
- Развёрнутый — представляет сумму двух прямых элементов.
- Выпуклый — угол между лучами составляет больше 180 градусов, но меньше 360.
- Полный — равняется 360 градусам.
Располагаясь на плоскости, по отношению друг к другу углы могут быть смежными или вертикальными. Согласно определению, смежными углами называют такую пару, у которой одна сторона принадлежит обеим фигурам, а два других луча образуют прямую линию. Вертикальными же считаются углы, стороны которых дополняют друг друга до прямых линий. Они всегда градусно равны.
Единицей измерения разворота фигуры является градусная мера. Если в нём содержится нецелое количество градусов, то используются минуты и секунды. Так, в одном градусе содержится 60 минут, а в одной минуте 60 секунд.
Острые, тупые и прямые углы
Рассмотрим три возможные ситуации на предмет типов углов по градусам, которые могут встретиться в составе смежных.
Один из углов — острый. Если градусная мера одного угла $0^\circ\leq{\angle{\alpha}}<90^\circ$, то второй угол в паре смежных получается тупым (в границах $90^\circ<x<180^\circ$).
Один из углов — тупой. Известно, что один из углов в паре $90^\circ<\angle{\alpha}<180^\circ$. В таком случае второй, с ним смежный, будет иметь градусную меру $0^\circ\leq{x}<90^\circ$.
Один из углов — прямой. Если один из углов имеет градусную меру $90^\circ$, то второй также равняется $90^\circ$. Угол, смежный с прямым, тоже будет прямым.
{"questions":,"explanations":["","","","Угол, смежный с тупым, может быть тупым? Их сумма явно выйдет за границы $180^\\circ$, что будет противоречить теореме о сумме смежных углов.","«Острый угол, смежный с острым углом» — некорректная часть утверждения. Два острых угла в сумме будут давать значение $
Свойства смежных углов:
1. сумма размеров смежных углов равна 180°.
2. пересечение двух прямых дает две пары смежных углов.
3. углы, касательные к прямому углу, являются прямыми углами. Эти углы равны между собой.

4.В паре смежных углов один угол всегда тупой, а другой всегда острый или оба угла прямые.
5. синусоиды смежных углов равны.
6. теорема косинуса и тангенсы смежных углов имеют одинаковую величину, но противоположные знаки.
Примечание: Фотографии https: /www.pexels.com, https: /pixabay.com
Востребованные технологии
- Концепция инновационного развития общественного производства – осуществления Второй индустриализации России на период 2017-2022 гг. (106 945)
- Экономика Второй индустриализации России (103 199)
- Этилен (этен), получение, свойства, химические реакции (29 510)
- Программа искусственного интеллекта ЭЛИС (29 469)
- Метан, получение, свойства, химические реакции (26 571)
- Крахмал, свойства, получение и применение (26 035)
- Природный газ, свойства, химический состав, добыча и применение (25 163)
- Целлюлоза, свойства, получение и применение (24 308)
- Пропилен (пропен), получение, свойства, химические реакции (23 556)
- Прямоугольный треугольник, свойства, признаки и формулы (23 269)
О чём данный сайт?
Сайт посвящен научным разработкам автора в области экономики и научным идеям осуществления второй индустриализации России.
Включает:- Экономика второй индустриализации России — Теории, методологии и инструменты инновационного развития — Реализация второй индустриализации России — Организационные механизмы второй индустриализации России — Справочник по инновационным технологиям.
Продукты и технологии не продаются. Производители и изобретатели! Вы должны связаться с ними напрямую!
Мы ведем переговоры с отечественными производителями и изобретателями инновационных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Применение второй индустриализации в России базируется на качественно новых научных основаниях (теория, методология и инструментарий), разработанных авторами.
Конечным результатом второй индустриализации России является рост благосостояния всех членов общества — среднего человека, предприятия и государства.
Вторая индустриализация России — это совокупность научных, технических и других инновационных идей, планов и разработок, которые могут быть широко применены в практике хозяйственной деятельности в короткий срок (3-5 лет) и обеспечивают качественно новые прогрессивные сдвиги. общества в ближайшие 50-75 лет.
Россия, первой сделавшая это сложное открытие, станет лидером мирового сообщества, что в других странах останется невозможным в течение столетий.
Интересный факт
Связь между математикой и музыкой.
‘Учитывая искусство и науку, их взаимосвязи и противоречия, мы приходим к выводу, что математика и музыка находятся на крайних полюсах человеческой психики. Человечество было создано в области науки и искусства». Х. Нейгауза кажется очень абстрактной областью математики. Однако связь между математикой и музыкой исторически и внутренне зависима, несмотря на то, что математика является наиболее абстрактной наукой и музыкой. Соглашение было основано на этой музыкальной системе, которая определяла приятное звучание струны, и двух законах, названных в честь двух великих ученых — Пифагора и Архетипа. Эти законы таковы: 1. Если две звуковые струны ассоциируются как целые числа по длине, определяют согласие и образуют треугольное число 10 = 1+2+3+4, т.е. 1:2, 2:3, 3:4. Более того, чем меньше число n в соотношении n: (n+1) (n = 1,2,3), тем более созвучны получаемые интервалы. 2. Частота колебаний w звуковой струны обратно пропорциональна длине L. w = a:l, где a — коэффициент, характеризующий физические свойства струны.
(Мы также предлагаем забавную пародию на двух математиков, которые не согласны =)
Математика — это язык, понятный всему миру
Математика – это язык логики и точности. Она помогает структурировать и систематизировать информацию, а также строить логические цепочки рассуждений. Математика учит нас анализировать, решать проблемы и находить оптимальные решения. Она развивает нашу способность к абстрактному мышлению, критическому мышлению и логическому мышлению.
Одной из особенностей математики является ее универсальность. Независимо от языка, на котором говорит человек, математические символы и формулы остаются одинаковыми. Это позволяет математике быть понятной и доступной для всех, вне зависимости от культурных или языковых различий.
Благодаря своей универсальности, математика используется во многих сферах жизни – от технических наук до экономики и финансов. Она является основой для развития науки и техники. Математические расчеты помогают прогнозировать и моделировать различные процессы и явления в мире, что позволяет нам лучше понимать окружающую нас реальность.
Математика открывает перед нами целый мир занимательных головоломок и задач. Ее изучение не только развивает наши умственные способности, но и приносит ощущение удовлетворения от решения сложных задач и открытия новых знаний. Мы можем применять математические методы и приемы не только для решения задач в учебе, но и в повседневной жизни. Они помогают нам принимать рациональные решения, анализировать информацию и предсказывать результаты действий.
Математика – это не просто предмет, а увлекательное исследование и погружение в мир абстрактных понятий и логических законов. Она помогает нам понять окружающий нас мир и открывает перед нами неисчерпаемый источник знаний и возможностей. Именно поэтому она стала моим любимым предметом.
Применение смежных углов
Смежные углы – это два угла, которые имеют общую сторону и вершину. Они располагаются рядом друг с другом и смотрят в разные стороны.
Зная, что смежные углы равны, мы можем применять это свойство в решении геометрических задач. Например, если в треугольнике один из углов равен другому смежному углу, мы можем найти меру третьего угла, используя свойство суммы углов треугольника.
Также смежные углы позволяют нам находить углы при пересечении прямых. Например, если две прямые пересекаются, то углы, создаваемые этим пересечением и лежащие на одной стороне от пересекающейся прямой, будут смежными углами и равны между собой.
Кроме того, знание свойства равенства смежных углов может помочь в решении задач на построение геометрических фигур. Например, чтобы построить равнобедренный треугольник, нужно провести высоту к одной из сторон и затем построить смежные углы, которые будут равны между собой.
Таким образом, понимание свойства равенства смежных углов позволяет нам решать множество задач в геометрии и создавать различные геометрические фигуры и конструкции.


























