Биссектриса угла

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

. То есть, если угол между линиями A .

равен φ, то мы говорим, что угол между пересекающимися прямыми a и b равен φ.

3. Смотрите статистику просмотра видеоуроков учениками.

Конспект урока «Угол между прямыми»

Докажем, что угол между двумя пересекающимися прямыми не зависит от выбора точки M

Возьмем любую другую точку M₁A₁и через него линии a₁и б

параллельны a и b соответственно. Пусть угол между прямыми a

и б

быть

и угол между линиями a

и б₁один₁B₁Если линии a

лежат в одной плоскости, то по свойству углов пересечения для параллельных прямых угол α₁B₁равна φ и равна углу a.₁B₁Пусть теперь линии a

и б₁.

которые пересекаются в точке M₂лежат в одной плоскости. И пусть линии₂и б₂которые пересекаются в точке M₁и б₁Поскольку линия a₁параллельна прямой a и прямой a₂и б₂Поскольку линия a₂.

также параллельны. Поскольку линия b₁, b₁, a₂, b₂параллельна прямой b и прямой b₁параллельна прямой b, то согласно принципу параллельности прямых в пространстве, прямые b₂.

Ответственный, настойчивый, харизматичный, последовательный, очень хороший уровень подготовки, терпеливый. Наша дочь очень довольна и, очевидно, Intere₁Большое спасибо. Я очень рада, что мы нашли этот источник для обучения. Ирина Сергеевна объясняет все быстро, четко и динамично. Всего за несколько уроков мы наверстали упущенную химию и продвинулись вперед. Мы обязательно обратимся снова в будущем.₂Елизавета делает хорошие успехи и учится с радостью и энтузиазмом. Римма Николаевна очень интересно преподносит материал. Мне очень нравится этот учитель, мы очень довольны уроками.₁Нам нравилась Нина Ивановна, хороший человек и прекрасный учитель. Она очень ответственная, трудолюбивая и знающая. Она сразу же нашла подход к своему ученику. Она может доходчиво объяснить любую тему. Учитель, в отличие от многих других преподавателей, не тратит время впустую, а действительно помогает.₂Она была прекрасным преподавателем и нашла подход с первых же уроков. Она объяснила все очень четко и понятно. Моему ребенку она очень нравится, и он просит о дополнительных занятиях.₁Здравствуйте, Рита Ивановна очень профессионально оценила все пробелы в знаниях моего сына, и мы бы с удовольствием продолжили обучение с ней! Уроки очень хорошие, преподаватель все понятно объясняет, я рекомендую ее всем.₂Спасибо, Ольга Ольга, за урок на каникулах. Желаю ей здоровья и благополучия, побольше счастливых событий в жизни, процветания, успехов и удачи в ее нелегком и нужном труде. Спасибо за урок, мне он очень понравился!₁и б₂

Биссектриса и параллельность, биссектрисы смежных углов

Тот факт, что биссектриса делит угол пополам, в каких-то случаях приводит к совершенно неожиданным результатам. Вот, например,

Случай 1

Здорово, правда? Давай поймём, почему так.

С одной стороны, — мы же проводим биссектрису!

Но, с другой стороны, — как накрест лежащие углы (вспоминаем тему ).

И теперь выходит, что; выкидываем середину: ! — равнобедренный!

Случай 2

Представь треугольник (или посмотри на картинку)

Давай продолжим сторону за точку. Теперь получилось два угла:

• — внутренний угол
• — внешний угол — он же снаружи, верно?

Так вот, а теперь кому-то захотелось провести не одну, а сразу две биссектрисы: и для, и для. Что же получится?

А получится прямоугольный!

Удивительно, но это именно так.

Разбираемся.

Как ты думаешь, чему равна сумма?

Конечно же, — ведь они все вместе составляют такой угол, что получается прямая.

А теперь вспомним, что и -биссектрисы и увидим, что внутри угла находится ровно половина
от суммы всех четырех углов: и — — то есть ровно. Можно написать и уравнением:

Итак, невероятно, но факт:

Угол между биссектрисами внутреннего и внешнего угла треугольника равен.

Случай 3

Видишь, что здесь все так же, как и для внутреннего и внешнего углов?

Или ещё раз подумаем, почему так получается?

Снова, как и для смежных углов,

(как соответственные при параллельных основаниях).

И опять, составляют ровно половину
от суммы

Вывод:
Если в задаче встретились биссектрисы смежных
углов или биссектрисы соответственных
углов параллелограмма или трапеции, то в этой задаче непременно
участвует прямоугольный треугольник, а может даже и целый прямоугольник.

тригонометрия — Биссектриса угла в прямоугольном треугольнике

спросил 5 лет, 10 месяцев назад

Изменено
3 года, 2 месяца назад

Просмотрено
24к раз

$\begingroup$

В прямоугольном треугольнике катеты, примыкающие к прямому углу, равны $a$ и $b$. Докажите, что длина биссектрисы (прямого угла) равна $$\frac{a\cdot b\cdot \sqrt{2}}{a+b}.$$

Подходя к этому вопросу, я был очень озадачен тем, как я получу это выражение.

Кроме того, я не мог понять, откуда берется $\sqrt{2}$, кроме как от синуса или косинуса $45$ градусов (от биссектрисы).

• тригонометрия
• треугольники

$\endgroup$

1

$\begingroup$

Элементарное решение: На следующем рисунке $|BC|=a,|CA|=b,|AB|=c$ и $$ биссектриса угла. Нарисуем квадрат $CEDF$ и $|CE|=x$. Итак, $|BE|=a-x$ и $|CD|=x\sqrt2$. Теперь $\triangle ABC \sim \triangle DBE$ и $$\dfrac{b}{a}=\dfrac{x}{a-x} $$ 9\circ})}=\frac{ab}{c(\frac{a}{c} \cdot \frac{1}{\sqrt{2}}+\frac{b}{c}\cdot\frac{ 1}{\sqrt{2}})}=\frac{\sqrt{2}ab}{a+b}.$$

$\endgroup$

$\begingroup$

Просто используйте тот факт, что площадь треугольника PQR равна PQsinx, где x — угол между P и Q. И здесь сумма площадей двух треугольников (образованных биссектрисой угла) равна 1/2*AB*BC (т.

$\endgroup$

Свойства

Построение биссектрисы

Свойства точек пересечения биссектрис

• Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
• Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
• Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
• Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.

Свойства, связанные с углами

• Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
• Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
• Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.

Свойства биссектрис равнобедренного треугольника

• Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
• Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
• В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
• Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный.
• У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
• У равностороннего треугольника все три внутренние биссектрисы равны.

Свойства оснований биссектрис

Точка пересечения биссектрисы со стороной треугольника называется основанием биссектрисы.

BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.

• Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть BDCD=ABAC{\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}} или BDAB=CDAC{\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}.
• Теорема о биссектрисе — частный случай теоремы Штейнера.
• Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
• Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
• Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
• Через точку Фейербаха проходит окружность, проведённая через основания биссектрис .

Свойства осей биссектрис

• Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
• Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис.

Другие свойства

• Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
• Расстояния от сторон угла до любой точки биссектрисы одинаковы.
• Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно, причём даже при наличии трисектора.
• Три внешние биссектрисы любого треугольника пересекаются в трёх разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трёх внешних биссектрис исходного треугольника.

Все о параллелограмме

Чем отличаются свойства от признаков?Свойства нельзя путать с признаками, хоть они и очень похожи. Например, свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, а признаки предназначены для выявления параллелограммов среди четырехугольников.

Свойства параллелограмма

1. Противолежащие стороны равны.

2. Противолежащие стороны параллельны.

3. Диагонали пересекаются и точкой пересечения делятся пополам.

4) Сумма углов прилежащих к любой стороне равна 180°. 

Это так, потому что, как в примере на картинке, стороны AD и BC — параллельные прямые, а AB — секущая. Следовательно, по свойству двух параллельных прямых и секущей, это односторонние углы и их сумма равна 180°.

5) Противолежащие углы попарно равны. Это доказывается через третий признак равенства треугольников, ведь, например, у треугольников ABD и BDC все стороны равны, а значит и углы тоже.

Теперь перейдем к признакам параллелограмма. Это то, что нам помогает понять, что четырехугольник является параллелограммом.

У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.

Признаки параллелограмма

1. Две противоположные стороны четырехугольника параллельны и равны.

2. Противоположные стороны четырехугольника попарно равны.

3. Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

Теперь рассмотрим биссектрису в параллелограмме.

Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Рассмотрим два полезных факта, связанных с биссектрисой в параллелограмме.

1. Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник. 

Это тоже доказывается с помощью параллельных прямых. Рассмотрим две параллельные прямые: AD и BC, а также секущую AF. Углы FAD и BFA равны, так как они накрест лежащие. А так как AF — биссектриса, то углы BAF и FAD, углы FAD и BFA тоже, значит и BAF = BFA. Следовательно, треугольник BAF — равнобедренный.

2. Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.

Мы почти закончили изучение параллелограмма. Осталось только рассмотреть формулы для нахождения площади. Их всего три.

1. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

2. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

3. Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Какая фигура является антагонистом параллелограмма?Есть такая фигура, которая называется «антипараллелограмм». Это плоский и самопересекающийся четырехугольник, в котором две противоположные стороны равны между собой, но не параллельны. Напомним, что у параллелограмма противоположные стороны равны и параллельны между собой.

Мы рассмотрели всю теорию, связанную с параллелограммом. Давайте теперь решим задание для закрепления материала.

Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.Задание. Стороны параллелограмма равны 10 и 15. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение. Примем искомую высоту за x. Как мы уже знаем, площадь параллелограмма можно найти с помощью высоты и стороны, к которой эта высота проведена. Соответственно, с помощью этой формулы мы и можем найти x:\(S = a*h_1=b*h_2\)\(S=10*12=15*h_2\)\(h_2=\frac{10*12}{15}\)\(h_2=8\)Ответ: 8

На этом мы закончили изучение параллелограмма, так что можем двигаться дальше!

Длина частей биссектрис в треугольнике

• Расстояние от вершины C до центра вписанной окружности равно \displaystyle{ l_{c0}=\frac{r}{\sin(\frac{\gamma}{2})}= \sqrt{(p-c)^2 + r^2}= \sqrt{ab — 4Rr} }, где R и r — радиусы описанной и вписанной окружностей, а γ — угол вершины C.
• Формулы последнего пункта по сути дают длину части биссектрисы от вершины до точки их пересечения (до центра вписанной окружности или до инцентра).
• Эту формулу и формулу для второй части внутренней биссектрисы можно также найти на основе следующего факта:
• Инцентр делит внутреннюю биссектрису угла \displaystyle{ A } в отношении \displaystyle{ \frac{b+c}{a} }, где \displaystyle{ a }, \displaystyle{ b }, \displaystyle{ c } — стороны треугольника.

Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон. 

Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

S = p∗r

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5

Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;. 6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

У правильного треугольника все внешние биссектрисы параллельны сторонам;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

Углы в треугольнике

Видео по теме

Мнемоническое правило «биссектриса-это крыса, которая бегает по углам и делит их пополам» описывает суть понятия, но не дает рекомендаций по построению биссектрисы. Чтобы ее начертить, кроме правила вам понадобится циркуль и линейка.

Инструкция

Допустим, что вам нужно построить биссектрису угла A. Возьмите циркуль, поставьте его острием в точку A ( угла) и начертите окружность любого . Там, где она пересечет стороны угла, поставьте точки B и C.

Замерьте радиус первой окружности. Начертите еще одну, с таким же радиусом, поставив циркуль в точку B.

Проведите следующую окружность (по размеру равную предыдущим) с центром в точке C.

Все три окружности должны пересечься в одной точке – назовем ее F. С помощью линейки проведите луч, проходящий через точки A и F. Это и будет искомая биссектриса угла A.

Существует несколько правил, помогут вам в нахождении . Например, она противоположную в , равном отношению двух прилежащих сторон. В равнобедренном

СВОЙСТВА БИССЕКТРИСЫ

Свойство биссектрисы: В треугольнике биссектриса делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.

Биссектриса внешнего угла Биссектриса внешнего угла треугольника пересекает продолжение его стороны в точке, расстояния от которой до концов этой стороны пропорциональны соответственно прилежащим сторонам треугольника. C B A D

Формулы длины биссектрисы:

Формула нахождения длин отрезков, на которые биссектриса делит противоположную сторону треугольника

Формула нахождения отношения длин отрезков, на которые биссектриса делится точкой пересечения биссектрис

Задача 1. Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 3:2, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 12 см.

Решение Воспользуемся формулой для нахождение отношения длин отрезков, на которые биссектриса делится точкой пересечения биссектрис в треугольнике:   a + c = = 18  P ∆ АВС = a + b + c = b +(a + c) = 12 + 18 = 30. Ответ: P = 30см.

Задача 2 . Биссектрисы BD и CE ∆ ABC пересекаются в точке О. АВ=14, ВС=6, АС=10. Найдите О D .

Решение. Воспользуемся формулой для нахождения длины биссектрисы: Имеем: BD = BD = = По формуле отношения отрезков, на которые биссектриса делится точкой пересечения биссектрис: l = . 2 + 1 = 3 части всего.

это 1 часть  OD = Ответ: OD =

Задачи В ∆ ABC проведены биссектрисы AL и BK . Найдите длину отрезка KL , если AB = 15, AK =7,5, BL = 5. В ∆ ABC проведена биссектриса AD , а через точку D прямая, параллельная AC и пересекающая AB в точке Е. Найдите отношение площадей ∆ ABC и ∆ BDE , если AB = 5, AC = 7. Найдите биссектрисы острых углов прямоугольного треугольника с катетами 24 см и 18см. В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 см. Определить площадь треугольника.

5. В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20 см. Найдите биссектрису угла при основании треугольника. 6. Найдите биссектрису прямого угла треугольника, у которого катеты равны a и b . 7. Вычислите длину биссектрисы угла А треугольника ABC с длинам сторон a = 18 см, b =15 см, c = 12 см. 8. В треугольнике ABC длины сторон AB , BC и AC относятся как 2:4:5 соответственно. Найдите, в каком отношении делятся биссектрисы внутренних углов в точке их пересечения.

Ответы: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: Ответ: AP = 6 AP = 10 см. KL = CP =

Геометрия — одна из самых сложных и запутанных наук. В ней то, что кажется на первый взгляд очевидным, очень редко оказывается правильным. Биссектрисы, высоты, медианы, проекции, касательные — огромное количество действительно непростых терминов, запутаться в которых очень легко.

На самом деле при должном желании можно разобраться в теории любой сложности. Когда дело заходит о биссектрисе, медиане и высоте, нужно понимать, что они свойственны не только треугольникам. На первый взгляд это простые линии, но у каждой из них есть свои свойства и функции, знание которых существенно упрощает решение геометрических задач. Итак, что же такое биссектриса треугольника?

Биссектриса в равнобедренном треугольнике.

Не боишься слова «теорема»? Если боишься, то — зря. Теоремой математики привыкли называть всякое утверждение, которое можно как-то вывести из других, более простых утверждений.

Так вот, внимание, теорема!

Докажем
эту теорему, то есть поймём, почему же так получается? Посмотри на равнобедренный.

Давай посмотрим на них внимательно. И тогда увидим, что

1. — общая.

А это значит (скорее вспоминай первый признак равенства треугольников!), что.

Ну и что? Хочется тебе так сказать? А то, что мы ещё не смотрели на третьи стороны и оставшиеся углы этих треугольников.

А вот теперь посмотрим. Раз, то совершенно точно и даже вдобавок, .

Вот и получилось, что

1. разделила сторону пополам, то есть оказалась медианой
2. , а значит, они оба по, так как (глянь ещё раз на рисунок).

Вот и оказалась биссектриса и высотой тоже!

Ура! Доказали теорему. Но представляешь, это ещё не всё. Верна ещё и обратная теорема:

Доказательство? Неужели тебе интересно? Читай следующий уровень теории!

А если неинтересно, то твердо запомни:

Зачем же это твердо запоминать? Как это может помочь? А вот представь, что у тебя задача:

Дано:
.

Найти:
.

Ты тут же соображаешь, биссектриса и, о чудо, она разделила сторону пополам! (по условию…). Если ты твердо помнишь, что так бывает только
в равнобедренном треугольнике, то делаешь вывод, что и значит, пишешь ответ: . Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!

А теперь следующее свойство. Готов?

Применение биссектрисы на практике

Биссектриса не является лишь абстрактным математическим понятием. На самом деле без знания этого термина и его сути невозможно обойтись во многих сферах: при строительстве крыши, при защите радиовысотомеров от радиолокационных ракет, при конструировании кораблей, при исследовании следов орудий взлома и так далее.

Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.

Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.

Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.

Разделение прямоугольника на равные части

Один из самых простых способов разделения прямоугольника на равные части – это использование перпендикулярного линейки и компаса. Для этого нужно провести две перпендикулярные линии, которые пересекаются в центре прямоугольника. Затем, используя компас, нарисуйте окружность с центром в центре прямоугольника. Эта окружность будет разделять прямоугольник на четыре равные части.

Если нужно разделить прямоугольник на большее количество частей, то можно использовать метод деления на половины. Сначала разделите прямоугольник пополам, проведя горизонтальную или вертикальную линию. Затем разделите каждую из получившихся половин на половины, проводя еще одну линию. Продолжайте этот процесс до получения нужного количества равных частей.

Если нужно разделить прямоугольник на равные части с помощью программного обеспечения, можно воспользоваться графическим редактором, таким как Adobe Photoshop или GIMP. Эти программы позволяют нарисовать линии разделения и автоматически распределить прямоугольник на равные части.

Разделение прямоугольника на равные части может быть полезным при решении математических и графических задач. Например, это может быть использовано для создания картины, лоскутного одеяла или мозаики. Также это может быть полезно при размещении объектов на веб-странице или при разработке интерфейса пользовательского приложения.

Свойства биссектрисы треугольника

Проведем в треугольнике АВС биссектрису ВК. После этого проведем прямую СМ, параллельную этой биссектрисе так, что точка М будет являться точкой пересечения продолжения стороны АВ.

Тогда два параллельных отрезка ВК и МС отсекут от сторон угла ВАС пропорциональные отрезки. То есть: АВ:АК=ВМ:КС. Докажем, что ВМ=ВС. Для этого посмотрим на треугольник ВМС. Угол АВК равен углу ВМС, как соответственные углы параллельных прямых при секущей АМ. С другой стороны угол КВС равен углу ВСМ, как накрест лежащие при параллельных прямых и секущей ВС. Но при этом угол АВК равен углу КВС, так как ВК – это биссектриса. Запишем все в виде равенств для большего понимания.

$$АВК = ВМС$$

$$КВС = ВСМ$$

$АВК = КВС$, значит углы ВМС и МСВ равны, а треугольник МВС – равнобедренный. Тогда $ВМ=ВС$ и $АВ:АК=ВС:СК$. Что и требовалось доказать.

Рис. 1. Первое свойство

Биссектриса равноудалена от сторон угла, в котором она проведена.

Это свойство не биссектрисы треугольника, а любой биссектрисы, поэтому ее доказательство проще рассматривать на рисунке угла.

Нарисуем угол АВС и проведем в нем биссектрису ВМ. Расстояние от биссектрисы до стороны в любой точке это перпендикуляр. Поэтому выберем произвольную точку на биссектрисе. Назовем ее D и опустим перпендикуляр на сторону АВ в точку Р и на сторону ВС в точку N. Тогда мы получим два прямоугольных треугольника: DРВ и DNB, равные между собой по гипотенузе ВD, которая будет общей стороной треугольников, и острому углу, так как угол PBD равен углу DBN, так как ВМ – биссектриса. Значит, и стороны PD=DN – как соответственные элементы. Доказательство простое, но изящное. Знание этого свойство поможет в доказательстве следующей теоремы.

Рис. 2. Второе свойство

Биссектрисы треугольника пересекаются в одной точке, и эта точка служит центром вписанной окружности. Это доказывается очень просто, необходимо из точки пересечения опустить перпендикуляры к каждой стороне.

Рис. 3. Третье свойство

Что мы узнали?

Мы узнали, что такое биссектриса треугольника и чем она отличается от обычной биссектрисы. Выделили три свойства биссектрисы треугольника, которые пригодятся при решении задач и доказательстве теорем.

1. /5

   Вопрос 1 из 5

   Что такое биссектриса?

   • Луч, делящий угол пополам.
   • Луч, исходящий из середины отрезка и перпендикулярный ему
   • Отрезок, исходящий из вершины треугольника и перпендикулярный противоположной стороне
   • Отрезок, исходящий из вершины треугольника и делящий противоположную сторону пополам

Формулы, теоремы и свойства элементов треугольника. Справочник репетитора по математике

Теоретичесикие шпаргалки по элементарной геометрии для занятий с репетитором по математике. Базовый школьный уровень. Свойства элементов треугольника. В помощь для решению задач по всему курсу планиметрии. Для тренировки решения задач С4 на ЕГЭ по математике.

1) Определение тригонометрических функций острого угла в прямоугольном треугольнике и теорема Пифагора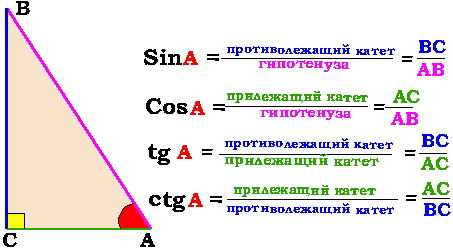Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов, то есть

2) Формулы площади треугольника

• 3) Подобие треугольников
• Определение: два треугольника называются подобными, если у них соответствующие углы равны и соответствующие стороны пропорциональны, то есть
  и
• Обозначение:
• 4) Признаки подобия двух треугольников
• 1-й признак: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
• Коротко: если , то
• 2-й признак:если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, образованные этими сторонами равны, то треугольники подобны
• Коротко: если и , то
• 3-й признак:если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то треугольники подобны, то есть
• Коротко: если , то
• 5) Свойства подобных треугольников
• если , то
• , где
• и  — любые соответствующие медианы (проведенные к соответствующим сторонам)
• и  — любые соответствующие биссектрисы (проведенные к соответствующим сторонам)
• и  — любые соответствующие высоты (проведенные к соответствующим сторонам)
• 6) Подобие прямоугольных треугольников. Высота, проведенная из вершины прямого угла
• Теорема: высота в прямоугольном треугольнике, поведенная из вершины прямого угла образует два треугольника, подобных исходному. Для катетов и высоты исходного треугольника верны следующие формулы:
• 7) Свойство медиан в треугольнике.
• Теорема 1: Все медианы треугольника пересекаются в одной точке (центр тяжести треугольника) и делятся этой точкой в отношении 2:1, считая от вершин. То есть
• Теорема 2: Каждая медиана, проведенная в треугольнике делит этот треугольник на две равновеликие части (на два треугольника с равными площадями),
• То есть
• Теорема 3: все три медианы делят треугольник на 6 равновеликих треугольников, то есть
• Свойство биссектрис в треугольнике Теорема 1: Каждая биссектриса угла в треугольнике делит его противолежащую сторону на отрезки, пропорциональные к двум другим сторонам треугольника.
• То есть

Теорема 2: Все биссектрисы в треугольнике пересекаются в одной точке, которая является центром вписанной с треугольник окружности. В любой треугольник можно вписать окружность и только одну.

9) Свойство точки пересечения серединных перпендикуляров к сторонам треугольника:

Теорема: все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке и эта точка является центром описанной около треугольника окружности. Вокруг любого треугольника можно описать окружность и только одну.

1. 10) Теорема о разделительном отрезке в треугольнике

   Теорема: Отрезок, соединяющий вершину треугольника с противоположной стороной делит ее на отрезки, пропорциональные площадям образованных треугольников.

2. То есть
3. 11) Средняя линия треугольника
4. Теорема: Средняя линия треугольника, соединяющая середины двух его сторон параллельна третьей стороне и равна ее половине.
5. То есть и
6. 12) Теорема синусов и теорема косинусов
7. Теорема синусов: Cтороны треугольника пропорциональны синусам противолежащих углов и каждое отношение стороны к синусу равно диаметру описанной около треугольника окружности.
8. То есть
9. Теорема косинусов: Квадрат стороны треугольника равне сумме квадратов двух других сторон минус удвоенное произведение этих сторон на синус угла между ними, то есть
10. 13) Теорема Менелая

    Теорема: Произведение отношений отрезков, на которые произвольная прямая делит стороны треугольника (или их продолжения) равно единице

11. То есть

Комментарий репетитора по математике: несправедливо выброшенная теорема из школьного курса геометрии. Рекомендую репетиторам включить ее в подготовку, по крайней мере к вузовским олимпиадам и вступительным экзаменам по математике в МГУ. В программу ЕГЭ теорема Менелая не входит, но несколько типов задач без нее решаются очень сложно.

• 14) Теорема Чевы
• Теорема:если через вершины треугольника и произвольную внутреннюю точку провести отрезки к противоположным сторонам (чевианы), то их точки пересечения разделят стороны на отрезки, произведение отношений которых равно единице.
• То есть

Колпаков А.Н. Репетитор по математике.

Все о прямоугольнике

Начнем со свойств прямоугольника.

1. Все углы прямые.

2. Диагонали равны.

3. Стороны прямоугольника одновременно являются и его высотами.

4. Сумма квадратов двух прилежащих сторон равна квадрату диагонали. Это теорема Пифагора.

Со свойствами разобрались, теперь рассмотрим признаки.

1. Параллелограмм, имеющий хотя бы один прямой угол, — прямоугольник.

2. Параллелограмм, все углы которого равны, — прямоугольник.

3. Параллелограмм, диагонали которого равны, — прямоугольник.

4. Четырехугольник, у которого три прямых угла, — прямоугольник.

Так, а что там у нас с биссектрисами в прямоугольнике?

А с биссектрисами все достаточно легко. Биссектриса делит угол прямоугольника на два угла по 45° и пересекает одну из сторон прямоугольника.

Теперь рассмотрим два способа нахождения площади прямоугольника.

1. Площадь прямоугольника равна произведению двух соседних сторон.

2. Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.

Во что можно поиграть на уроках и вспомнить геометрию?1. Итак, запоминайте алгоритм.Бросаете два кубика.2. Делаете прямоугольник с размером сторон, которые сгенерировал кубик.3. Новый прямоугольник обязательно должен быть соединен с любым другим вашим прямоугольником.4. Если это ваш первый прямоугольник, то поместите его в любой угол, а соперник должен поместить свой в противоположный.5. Если у вас не получается создать прямоугольник с получившимися сторонами, то вы пропускаете ход.6. Игра заканчивается, когда вся территория занята. Побеждает тот, у кого наибольшая территория.

Давайте закрепим материал на примере.

Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.Задание. Площадь прямоугольника равна 20. Найдите его большую сторону, если она на 8 больше меньшей стороны.

Решение. Как мы уже знаем, площадь прямоугольника равна произведению длины на ширину. Примем одну сторону прямоугольника за x, тогда вторая равна x + 8.Тогда:\(S=x*(x+8)=20\)\(x^2+8x-20=0\)Решим квадратное уравнение:\(D=8^2-4*1*(-20)=64+80=144\)Корни уравнения:\(x_{1,2}=\frac{-8\pm 12}{2}\)Первый корень:\(x_1=\frac{-8+12}{2}=\frac{4}{2}=2\)Второй корень:\(x_2=\frac{-8-12}{2}=-\frac{20}{2}=-10\)Сторона не может иметь отрицательную длину, поэтому верный корень — первый. Это наименьший корень, а значит больший:\(x=2+8=10\)Ответ: 10

На этом заканчивается наша статья, но не тема четырехугольников. В следующей статье мы продолжим изучать их и узнаем про ромб и квадрат. Читайте здесь: «Параллелограмм. Часть 2».