Параллелограмм

Сопряжение окружностей (дуг)

Внешнее сопряжение дуг окружностей

Внешним сопряжением считается сопряжение, при котором центры сопрягаемых окружностей(дуг) O1( радиус R1) и O2 (радиус R2) располагаются за сопрягающей дугой радиуса R. На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.

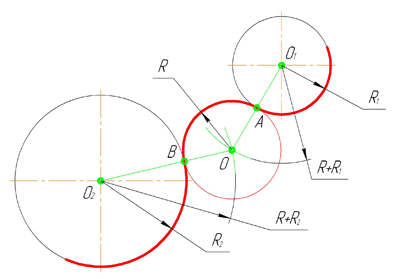
Внутреннее сопряжение дуг окружностей

Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно. После чего соединяем центры окружностей O1 и O2 прямыми линиями с центром сопряжения и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. Затем из центра сопряжения строим дугу сопряжения радиуса R и строим сопряжение.

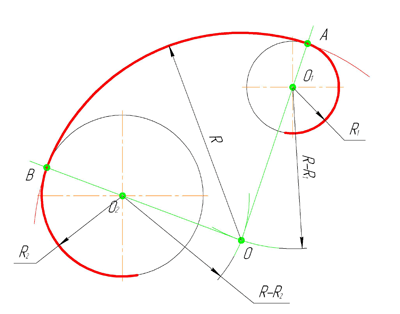
Смешанное сопряжение дуг окружностей

Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.

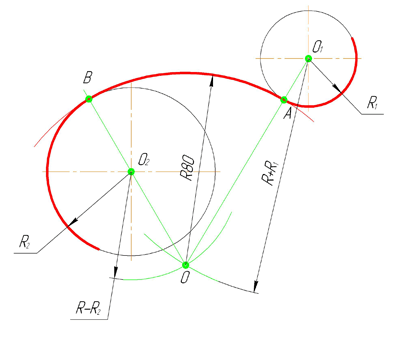
В данный момент вы не можете посмотреть или раздать видеоурок ученикам

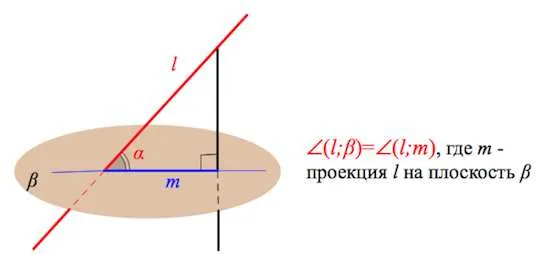
. То есть, если угол между линиями A .

равен φ, то мы говорим, что угол между пересекающимися прямыми a и b равен φ.

3. Смотрите статистику просмотра видеоуроков учениками.

Конспект урока «Угол между прямыми»

Докажем, что угол между двумя пересекающимися прямыми не зависит от выбора точки M

Возьмем любую другую точку M₁A₁и через него линии a₁и б

параллельны a и b соответственно. Пусть угол между прямыми a

и б

быть

и угол между линиями a

и б₁один₁B₁Если линии a

лежат в одной плоскости, то по свойству углов пересечения для параллельных прямых угол α₁B₁равна φ и равна углу a.₁B₁Пусть теперь линии a

и б₁.

которые пересекаются в точке M₂лежат в одной плоскости. И пусть линии₂и б₂которые пересекаются в точке M₁и б₁Поскольку линия a₁параллельна прямой a и прямой a₂и б₂Поскольку линия a₂.

также параллельны. Поскольку линия b₁, b₁, a₂, b₂параллельна прямой b и прямой b₁параллельна прямой b, то согласно принципу параллельности прямых в пространстве, прямые b₂.

Ответственный, настойчивый, харизматичный, последовательный, очень хороший уровень подготовки, терпеливый. Наша дочь очень довольна и, очевидно, Intere₁Большое спасибо. Я очень рада, что мы нашли этот источник для обучения. Ирина Сергеевна объясняет все быстро, четко и динамично. Всего за несколько уроков мы наверстали упущенную химию и продвинулись вперед. Мы обязательно обратимся снова в будущем.₂Елизавета делает хорошие успехи и учится с радостью и энтузиазмом. Римма Николаевна очень интересно преподносит материал. Мне очень нравится этот учитель, мы очень довольны уроками.₁Нам нравилась Нина Ивановна, хороший человек и прекрасный учитель. Она очень ответственная, трудолюбивая и знающая. Она сразу же нашла подход к своему ученику. Она может доходчиво объяснить любую тему. Учитель, в отличие от многих других преподавателей, не тратит время впустую, а действительно помогает.₂Она была прекрасным преподавателем и нашла подход с первых же уроков. Она объяснила все очень четко и понятно. Моему ребенку она очень нравится, и он просит о дополнительных занятиях.₁Здравствуйте, Рита Ивановна очень профессионально оценила все пробелы в знаниях моего сына, и мы бы с удовольствием продолжили обучение с ней! Уроки очень хорошие, преподаватель все понятно объясняет, я рекомендую ее всем.₂Спасибо, Ольга Ольга, за урок на каникулах. Желаю ей здоровья и благополучия, побольше счастливых событий в жизни, процветания, успехов и удачи в ее нелегком и нужном труде. Спасибо за урок, мне он очень понравился!₁и б₂

Параллельные и перпендикулярные прямые

Если наша полка в итоге висит идеально ровно по отношению к потолку, то с точки зрения планиметрии прямые, образованные полкой и потолком, будут называться параллельными. Параллельный — это непересекающийся: иными словами, такие прямые лежат в одной плоскости и при этом не пересекаются. Подробнее свойства параллельности мы разберем в курсе геометрии далее.

Пока просто дадим определение:

Разберем ситуацию, когда помимо двух параллельных прямых имеется перпендикулярная к одной из них. Начертим параллельные прямые $a$ и $b$. К прямой $a$ проведем перпендикуляр $c$ и достроим его до прямой $b$.

Если $c$ перпендикулярна к $a$, то она также перпендикулярна и к $b$, при условии, что $a$ и $b$ — параллельны. Доказать это можно, опять же, через метод доказательства от противного.

Связь между параллельностью и перпендикулярностью записать можно и «в обратном порядке»: если две (или более, — количество прямых может быть бесконечным) прямые перпендикулярны к третьей, то эти две прямые — параллельны.

{"questions":[{"content":"Что такое <b>«перпендикулярные прямые»?</b> `choice-1`","widgets":{"choice-1":{"type":"choice","options":,"answer":}}},{"content":"А что такое <b>«параллельные прямые»?</b> `choice-6`","widgets":{"choice-6":{"type":"choice","options":,"answer":}}},{"content":"Прямая $d$ перпендикулярна к прямой $h$. Как записать данной утверждение с помощью геометрической нотации? `choice-16`","widgets":{"choice-16":{"type":"choice","options":,"answer":}}},{"content":"Расшифруйте следующую запись: $AB\\perp{a}$. `choice-34`","widgets":{"choice-34":{"type":"choice","options":,"answer":}}},{"content":"Какая связь имеется между перпендикулярностью и параллельностью прямых? `choice-59`","widgets":{"choice-59":{"type":"choice","options":,"explanations":,"answer":}}}],"mix":1}

2.5. Следы прямой

След прямой – точка пересечения прямой с плоскостью проекций.

Прямая общего положения в общем случае может быть три следа:

• горизонтальный след M₁– точка пересечения прямой с горизонтальной плоскостью проекций π₁;
• фронтальный след N₂– точка пересечения прямой с фронтальной плоскостью проекций π₂;
• профильный  след L₃ – точка пересечения прямой с профильной плоскостью проекций π₃.

След прямой является точкой частного положения, поскольку он принадлежит плоскости проекций, следовательно, след прямой всегда совпадает с одной из своих проекций:

• горизонтальный след совпадает со своей горизонтальной проекцией M≡M₁,
• фронтальный – с фронтальной проекцией N≡N₂,
• профильный – с профильной проекцией L≡L₃ (Рисунок 2.10).

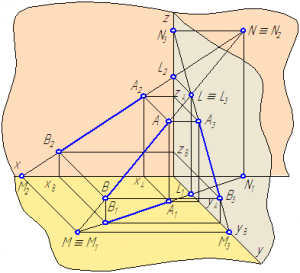
Рисунок 2.10 – Построение следов отрезка прямой АВ

Построим следы отрезка АВ с плоскостями проекций (Рисунки 2.10, 2.11).

Для построения горизонтального следа прямой АB необходимо:

1. Продолжить фронтальную проекцию прямой АB до пересечения с осью X, точка пересечения М₂ является фронтальной проекцией горизонтального следа;
2. Из точки М₂ провести линию проекционной связи до его пересечения с горизонтальной проекцией прямой АB или её продолжением. Точка пересечения М₁ и будет являться горизонтальной проекцией горизонтального следа, которая совпадает с самим следом М.

Чтобы построить фронтальный след отрезка АB прямой, необходимо:

1. Продолжить горизонтальную проекцию прямой АB до пересечения с осью X, точка пересечения N₁ является горизонтальной проекцией фронтального следа;
2. Из точки N₁ провести линию проекционной связи до его пересечения с фронтальной проекцией прямой АB  или ее продолжением. Точка пересечения N₂ и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.

Ниже приводим алгоритм построения следов отрезка прямой АВ:

A₁B₁ ∩ xO =N₁;       Y_N=0;                   N ∈ xOz (π₂)      ⇒      AB ∩ xOz=N

A₂B₂ ∩ xO =M₂;       Z_M=0;                  M ∈ xOy (π₁)     ⇒      AB ∩ xOy=M

A₁B₁ ∩ yO =L₁;        X_L=0;                   L ∈ yOz (π₃)     ⇒      AB ∩ yOz=L

A₂B₂ ∩ zO =L₂;

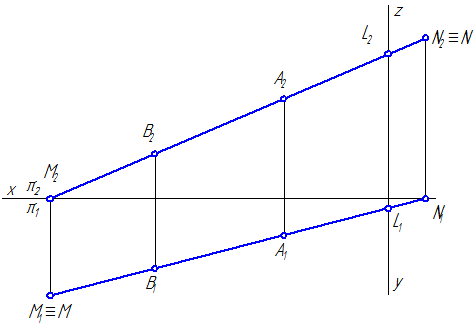Рисунок 2.11 – Эпюр построения следов отрезка прямой АВ

Прямая, параллельная одной из плоскостей проекций, не имеет следа на плоскости, которой она параллельна, и пересекает только две плоскости. Прямая, параллельная двум плоскостям проекций (проецирующая прямая), имеет только один след, совпадающий с проекцией прямой на плоскость, к которой она перпендикулярна.

Метод работы диагоналей:

Диагонали, пересекающиеся под прямым углом, представляют собой важный элемент в геометрии. Этот метод используется для нахождения и описания свойств разнообразных фигур, особенно при работе с параллелограммами. При пересечении диагоналей под прямым углом можно получить ряд следующих результатов:

1. Симметричность: диагонали, пересекающиеся под прямым углом, делят фигуру на две равные половины. Одинаковые части, образованные диагональю, являются зеркальными отражениями друг друга.
2. Пропорции: диагонали, пересекающиеся под прямым углом внутри фигуры, создают пропорциональные отношения. Например, отношение между отрезками диагоналей может быть использовано для вычисления площади фигуры.
3. Дополнительные углы: пересечение диагоналей под прямым углом позволяет найти новые углы в фигуре. Такие углы, как смежные, дополнительные или вертикальные, могут быть использованы для решения различных задач и определения других свойств фигуры.
4. Законы и свойства: с использованием метода работы диагоналей можно вывести множество геометрических законов и свойств, используемых для нахождения сторон, площадей, периметров и других параметров фигур.

Таким образом, диагонали, пересекающиеся под прямым углом, являются мощным инструментом для исследования и понимания геометрических фигур. Они позволяют находить новые свойства и решать различные задачи, делая геометрию более доступной и увлекательной.

Признаки параллелограмма

Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.

Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Докажем 1 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB || CD
• AB = CD

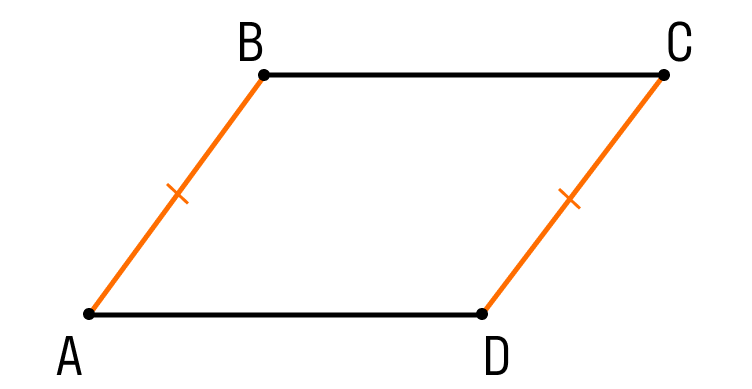
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.

Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.

Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:

1. AC — общая сторона;
2. По условию AB = CD;
3. ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

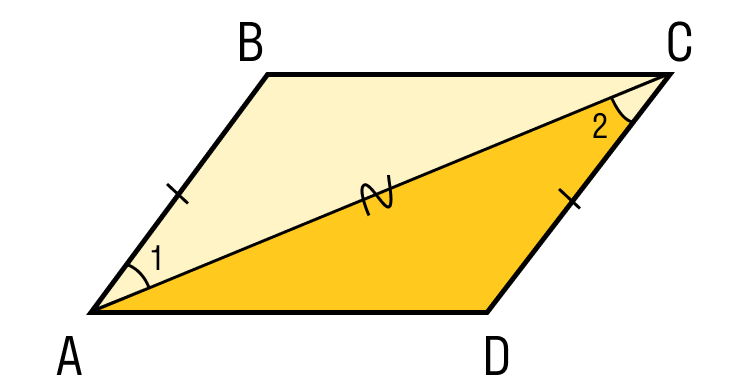
Шаг 3. Из равенства треугольников также следует:

Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.

Вот так быстро мы доказали первый признак.

Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Докажем 2 признак параллелограмма:

Шаг 1. Пусть в четырехугольнике ABCD:

• AB = CD
• BC = AD

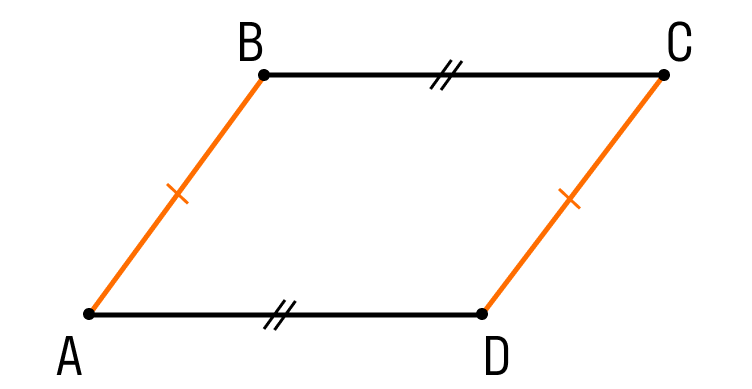
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:

• AC — общая сторона;
• AB = CD по условию;
• BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.

Шаг 3. Из равенства треугольников следует:

А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.

Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.

Доказали второй признак.

Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Докажем 3 признак параллелограмма:

Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:

• CO = OA;
• DO = BO;
• углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

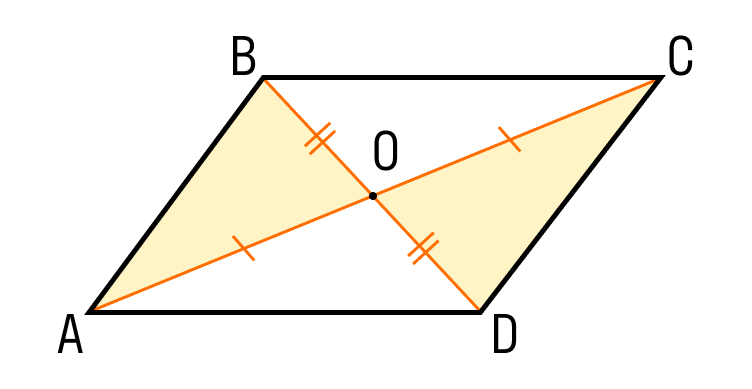
Шаг 2. Из равенства треугольников следует, что CD = AB.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).

Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.

Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.

Источник

Понимание углов диагоналей в геометрии

В геометрии диагональ — это отрезок, соединяющий две вершины некоторой фигуры. Когда диагонали пересекаются внутри фигуры, они образуют углы, которые играют важную роль в анализе и решении задач по геометрии.

Один из важных фактов о диагоналях, которые пересекаются внутри фигуры, заключается в том, что они пересекаются под углом. Это значит, что линия, проведенная через точку пересечения диагоналей и центр фигуры (если такой есть), образует прямой угол.

Понимание углов диагоналей важно при решении многих геометрических задач. Отношения углов между собой и отношения между сторонами фигуры могут быть использованы для нахождения неизвестных значений и доказательства свойств фигур

Например, при изучении свойств прямоугольников, понимание углов диагоналей позволяет нам получить следующие выводы:

1. Диагонали в прямоугольнике равны по длине и делят его на два равных треугольника.
2. Угол между диагоналями прямоугольника равен 90 градусам.
3. Длина диагонали прямоугольника можно найти с помощью теоремы Пифагора.

Таким образом, понимание углов диагоналей в геометрии является важным элементом для анализа и решения различных задач. Знание основных свойств фигур и смысл углов диагоналей помогут нам в работе с геометрическими фигурами, а также в их применении в реальном мире.

Построение перпендикулярной прямой

Сейчас мы с вами с помощью циркуля попробуем построить перпендикулярную прямую. Для этого у нас есть точка О и прямая а.

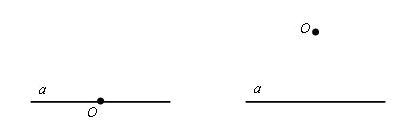
На первом рисунке изображена прямая на которой лежит точка О, а на втором данная точка не лежит на прямой а.

Теперь давайте по отдельности рассмотрим эти оба варианта.

1-й вариант

Вначале мы берем циркуль, ставим его в центр точки О и чертим окружность с произвольным радиусом. Теперь мы видим, что данная окружность пересекает прямую а в двух точках. Пускай это будут точки А и В.

Далее, мы берем и проводим окружности из точек А и В. Радиус этих окружностей будет АВ, а вот точка С будет точкой пересечения этих окружностей. Если вы помните, то в самом начале мы с вами получили точки А и В, когда чертили окружность и брали произвольный радиус.

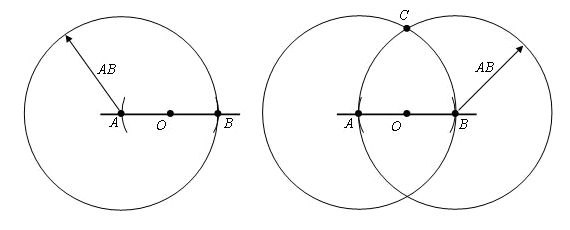
В итоге мы видим, что искомая перпендикулярная прямая проходит через точки С и О.

Доказательство

Для данного доказательства нас нужно провести отрезки AC и CB. И мы видим, что образовавшиеся треугольники равны: Δ ACO = Δ BCO, это следует из третьего признака равенства треугольников, то есть у нас выходит, что AO = OB, AC = CB, а СО общая по построению. Образовавшиеся углы ∠ COA и ∠ COB равны и оба имеют величину, равную 90 °. Из этого следует, что прямая CO перпендикулярна AB.

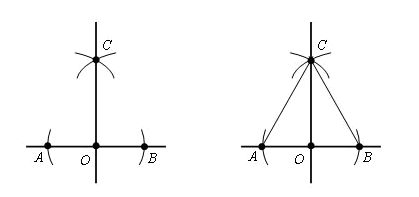
Отсюда мы можем сделать вывод, что углы, образованные при пересечении двух прямых являются перпендикулярными в том случае, если хотя бы один из них перпендикулярен, а это значит, что такой угол равен 90 градусам и является прямым.

2-й вариант

А сейчас давайте рассмотрим вариант построения перпендикулярной прямой, где данная точка не лежит на прямой а.

В этом случае мы с помощью циркуля из точки О проводим окружность с таким радиусом, чтобы эта окружность пересекала прямую а. А точки А и В пускай будут точками пересечения этой окружности с данной прямой а.

Далее, мы берем такой же радиус, но проводим окружности, центром которых будут точки A и B. Смотрим на рисунок и видим, что у нас появилась точка О1, которая также является точкой пересечения окружностей и лежит в полуплоскости, но отличной от той, в которой находится точка О.

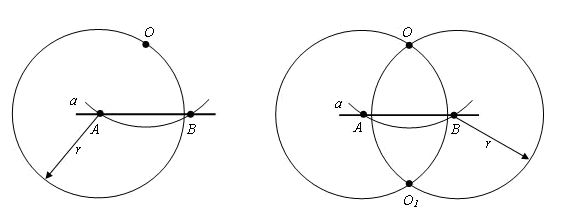
Следующее, что мы сделаем, так это через точки O и O1проведем прямую. Это и будет та перпендикулярная прямая, которую мы искали.

Доказательство

Припустим, что точкой пересечения прямых OO1 и AB является точка С.
Тогда треугольники AOB и BO1A равны по третьему признаку равенства треугольников и AO = OB = AO1 = O1B, а АВ является общей по построению. Из этого следует, что углы OAС и O1AC равны. Треугольники OAC и O1AC, следуя из первого признака равенства треугольников AO равняется AO1, а по построению, углы OAС и O1AC равны при общей AС. Следовательно, что угол OСA равен углу O1CA, но а так как они смежные, то значит прямые. Поэтому, делаем вывод, что OC является перпендикуляром, который опущенный из точки O на прямую a.

Вот так, только с помощью циркуля и линейки, можно легко построить перпендикулярные прямые

И не важно, где находится точка, через которую должен проходит перпендикуляр, на отрезке или вне этого отрезка, главное в этих случаях верно найти и обозначить первоначальные точки А и В.. Вопросы:

Вопросы:

1. Какие прямые называются перпендикулярными?
2. Какой угол между перпендикулярными прямыми?
3. Чем пользуються для построения перпендикулярных прямых?

ПредметиМатематикаМатематика 7 класс

Примеры

Две прямые заданы  уравнениями. Найти точку пересечения этих прямых и углы под которым они пересекаются

Основываясь на правилах для Расчет параметров прямой линии по заданным параметрам записываем  известные параметры

line_p A=11;B=-5;C=6,k=3/7;b=-5

получаем следующий результат

Уравнение первой прямой

y = 2.2 x + ( 1.2  )

Уравнение второй прямой

y = 0.4285714285714 x + ( -5  )

Угол пересечения двух прямых(в градусах)

-42.357454705937

Точка пересечения двух прямых

x = -3.5

y = -6.5

 

C помощью  построить график функции c помощью GeoGebra  построим наш график и мы получим вот такое изображение

 

 

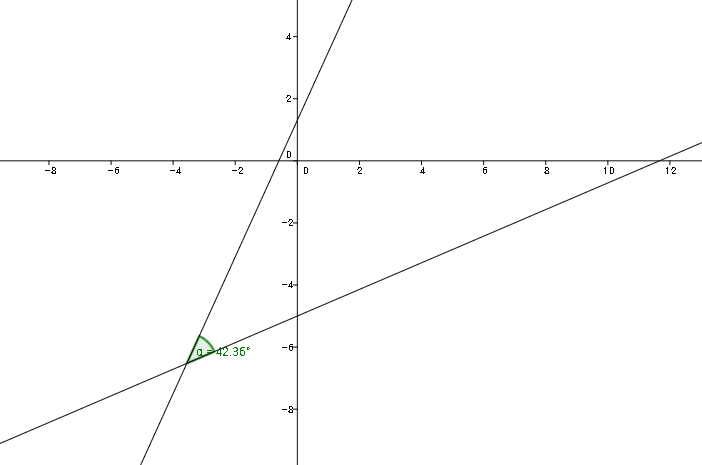
Не забудьте что параметры двух линий  разделяются запятой, а параметры каждой линии точкой с запятой.

Прямая проходит через две точки (1:-4) и (5:2) . Найти уравнение прямой, которая проходит через точку (-2:-8) и пересекает исходную прямую под углом 30 градусов.

Одна прямая нам известна, так как известны две точки через которые  она проходит.

Осталось определить уравнение второй прямой . Одна точка нам известна, а вместо второй указан угол, под которым первая прямая пересекает вторую. 

Вроде все известно, но тут главное не ошибится. Речь идет об угле(30 градусов) не между осью абсцисс и линией, а между первой и второй линией.

Для этого мы постим так. Определим параметры первой линии, и узнаем под каким углом она пересекает ось абсцисс.

Для этого воспользуемся Расчет параметров прямой линии по заданным параметрам

line xa=1;xb=5;ya=-4;yb=2

Параметры прямой линии  по заданным параметрам

Общее уравнение Ax+By+C = 0

Коэффициент А = -6

Коэффициент B = 4

Коэффициент C = 22

Уравнение прямой в отрезках  x/a+y/b = 1

Коэффициент a= 3.6666666666667

Коэффициент b = -5.5

Уравнение прямой c угловым коэфициентом  y = kx + b

Коэффициент k = 1.5

Угол наклона к оси ( в градусах) f = 56.309932474019

Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0

Коэффициент p = 3.0508510792386

Коэффициент q = 2.5535900500422

Расстояние между точками=7.211102550928

Расстояние от точки до прямой li =

Видим что первая линия пересекает ось под углом 56.309932474019 градусов.

В искходных данных не сказано как именно пересекает вторая линия, первую. Можно ведь построить две линии удовлетворяющих условиям, первая  повернутая на 30 градусов  ПО часовой стрелке, а вторая на 30 градусов ПРОТИВ часовой стрелке.

Давайте их и посчитаем

Если вторая линия повернута на 30 градусов ПРОТИВ часовой стрелке, то вторая линия будет иметь градус пересечения с осью абсцисс 30+56.309932474019 = 86.309932474019 градусов

Тогда мы можем посчитать любым способом уравнение второй прямой

line_p xa=-2;ya=-8;f=86.309932474019

Параметры прямой линии  по заданным параметрам

Общее уравнение Ax+By+C = 0

Коэффициент А = 23.011106998916

Коэффициент B = -1.4840558255286

Коэффициент C = 34.149767393603

Уравнение прямой в отрезках  x/a+y/b = 1

Коэффициент a= -1.4840558255286

Коэффициент b = 23.011106998916

Уравнение прямой c угловым коэфициентом  y = kx + b

Коэффициент k = 15.505553499458

Угол наклона к оси ( в градусах) f = 86.309932474019

Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0

Коэффициент p = -1.4809790664999

Коэффициент q = 3.0771888256405

Расстояние между точками=23.058912962428

Расстояние от точки до прямой li =

то есть наше уравнение второй линии есть y=15.505553499458x+23.011106998916

Проверим??

 

узнаем угол пересечения двух прямы х что мы нашли y=15.505553499458x+23.011106998916 и y=1.5x-5.5

 

line_p k=15.505553499458;b=23.011106998916,k=1.5;b=-5.5

 

Уравнение первой прямой

y = 15.505553499458 x + ( 23.011106998916  )

Уравнение второй прямой

y = 1.5 x + ( -5.5  )

Угол пересечения двух прямых(в градусах)

-29.999999999998

Точка пересечения двух прямых

x = -2.0357001242414

y = -8.553550186362

Как видно угол межуд прямыми именно такой какой нам задали в задании.

Задача решена.

Да, аналогично можно посчитать уравнение прямой которое было бы повернуто  на 30 градусов по часовой стрелке

Проверь себя

Задание 1.Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 30°. 

1. 40
2. 20
3. 10
4. 25

Задание 2.Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 60°.

1. \(8\sqrt{3}\)
2. \(6\)
3. \(6\sqrt{3}\)
4. \(4\)

Задание 3.У четырехугольника диагонали пересекаются под углом 30°, а его стороны попарно параллельны и равны. Что это за фигура?

1. Квадрат
2. Ромб
3. Прямоугольник
4. Параллелограмм

Задание 4.У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?

1. Квадрат
2. Ромб
3. Прямоугольник
4. Параллелограмм

Ответы: 1. – 2; 2. – 3; 3. – 4; 4. – 3.

Все о параллелограмме

Чем отличаются свойства от признаков?Свойства нельзя путать с признаками, хоть они и очень похожи. Например, свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, а признаки предназначены для выявления параллелограммов среди четырехугольников.

Свойства параллелограмма

1. Противолежащие стороны равны.

2. Противолежащие стороны параллельны.

3. Диагонали пересекаются и точкой пересечения делятся пополам.

4) Сумма углов прилежащих к любой стороне равна 180°. 

Это так, потому что, как в примере на картинке, стороны AD и BC — параллельные прямые, а AB — секущая. Следовательно, по свойству двух параллельных прямых и секущей, это односторонние углы и их сумма равна 180°.

5) Противолежащие углы попарно равны. Это доказывается через третий признак равенства треугольников, ведь, например, у треугольников ABD и BDC все стороны равны, а значит и углы тоже.

Теперь перейдем к признакам параллелограмма. Это то, что нам помогает понять, что четырехугольник является параллелограммом.

У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.

Признаки параллелограмма

1. Две противоположные стороны четырехугольника параллельны и равны.

2. Противоположные стороны четырехугольника попарно равны.

3. Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

Теперь рассмотрим биссектрису в параллелограмме.

Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

Рассмотрим два полезных факта, связанных с биссектрисой в параллелограмме.

1. Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник. 

Это тоже доказывается с помощью параллельных прямых. Рассмотрим две параллельные прямые: AD и BC, а также секущую AF. Углы FAD и BFA равны, так как они накрест лежащие. А так как AF — биссектриса, то углы BAF и FAD, углы FAD и BFA тоже, значит и BAF = BFA. Следовательно, треугольник BAF — равнобедренный.

2. Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.

Мы почти закончили изучение параллелограмма. Осталось только рассмотреть формулы для нахождения площади. Их всего три.

1. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

2. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

3. Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

Какая фигура является антагонистом параллелограмма?Есть такая фигура, которая называется «антипараллелограмм». Это плоский и самопересекающийся четырехугольник, в котором две противоположные стороны равны между собой, но не параллельны. Напомним, что у параллелограмма противоположные стороны равны и параллельны между собой.

Мы рассмотрели всю теорию, связанную с параллелограммом. Давайте теперь решим задание для закрепления материала.

Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.Задание. Стороны параллелограмма равны 10 и 15. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение. Примем искомую высоту за x. Как мы уже знаем, площадь параллелограмма можно найти с помощью высоты и стороны, к которой эта высота проведена. Соответственно, с помощью этой формулы мы и можем найти x:\(S = a*h_1=b*h_2\)\(S=10*12=15*h_2\)\(h_2=\frac{10*12}{15}\)\(h_2=8\)Ответ: 8

На этом мы закончили изучение параллелограмма, так что можем двигаться дальше!

Построение прямых углов на местности

Для построения прямых углов на местности применяют специальные приборы, простейшим из которых является экер. Экер представляет собой два бруска, расположенных под прямым углом и укрепленных на треножнике (рис. 7). На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны. Чтобы построить на местности прямой угол с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (прямая ОВ на рисунке 7). Получается прямой угол АОВ.В геодезии для построения прямых углов используются более совершенные приборы, например теодолит.

Задание.

По горизонтали:3. Отрезок прямой, соединяющий точку окружности с ее центром. 6. Утверждение, не требующее доказательства. 9. Конструкция, система мысли. 10. Вид четырехугольника. 15. Отрезок прямой, соединяющий две точки кривой. 16. Мера длины. 17. Тригонометрическая функция. 18. Точка пересечения диаметров окружности. 19. Тригонометрическая функция. 20. Часть окружности. 21. Старинная мера длины.По вертикали:1. Символ какого-либо алфавита. 2. Вид параллелограмма. 4. Хорда, проходящая через центр окружности. 5. Геометрический элемент. 7. Луч, делящий угол пополам. 8. Символ греческого алфавита. 10. Сумма длин сторон треугольника. 11. Вспомогательное предложение, используемое для доказательства. 12. Элемент прямоугольного треугольника. 13. Одна из замечательных линий треугольника. 14. Тригонометрическая функция.

Применение пересекающихся прямых в реальных задачах

Пересекающиеся прямые являются важным понятием в геометрии и математике в целом. Они имеют широкое применение в различных задачах и областях, как теоретических, так и практических.

1. Графики функций:

Пересечение графиков функций является ключевым моментом при решении уравнений и систем уравнений. Если графики двух функций пересекаются, то это означает, что существует точка (или точки), в которой значения этих функций равны друг другу. Это может быть полезно для определения корней уравнений или нахождения точек пересечения кривых.

2. Статистика и анализ данных:

Пересекающиеся прямые используются в анализе данных для определения зависимостей и взаимосвязей различных переменных. Например, в задачах линейной регрессии, где исследуется зависимость одной переменной от другой, пересечение прямой регрессии с осью ординат может указывать на начало или нулевое значение зависимой переменной.

3. Проектирование и архитектура:

Пересекающиеся прямые используются в проектировании и архитектуре для определения точек пересечения или соприкосновения различных элементов. Например, в строительстве пересечение линий может указывать на место сопряжения стен и потолка, или на точки пересечения строительных элементов.

4. Геодезия и навигация:

Геодезисты и навигаторы также используют пересекающиеся прямые для определения координат точек на местности. Путем измерений и пересечения линий, например, с помощью триангуляции, можно определить координаты точек и точное положение объектов.

Таким образом, пересекающиеся прямые являются мощным инструментом в решении различных задач и помогают анализировать и понимать различные взаимосвязи и зависимости в реальном мире.