Нормальное уравнение плоскости — описание, примеры, решение задач

Прямоугольные координаты вектора[править | править код]

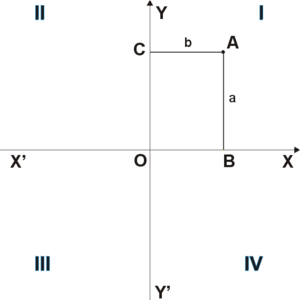
Рис. ??1

Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца.

Таким образом, например, координаты (x,y){\displaystyle (x,y)} на рис. 1 являются координатами вектора OA→{\displaystyle {\vec {OA}}}.

Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:

1. Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесённого так, что его начало совпадает с началом координат, — это координаты его конца.
2. Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.

Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси.

В прямоугольных координатах очень просто записываются все операции над векторами:

Сложение и умножение на скаляр:

a+b=(a1+b1,a2+b2,a3+b3,…,an+bn){\displaystyle \mathbf {a} +\mathbf {b} =(a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3},\dots ,a_{n}+b_{n})},

или:

(a+b)i=ai+bi,{\displaystyle (\mathbf {a} +\mathbf {b} )_{i}=a_{i}+b_{i},}

c a=(c a1,c a2,c a3,…,c an){\displaystyle c\ \mathbf {a} =(c\ a_{1},c\ a_{2},c\ a_{3},\dots ,c\ a_{n})},

или:

(c a)i=c ai.{\displaystyle (c\ \mathbf {a} )_{i}=c\ a_{i}.},

а отсюда и вычитание и деление на скаляр:

a−b=(a1−b1,a2−b2,a3−b3,…,an−bn){\displaystyle \mathbf {a} -\mathbf {b} =(a_{1}-b_{1},a_{2}-b_{2},a_{3}-b_{3},\dots ,a_{n}-b_{n})},

или:

(a−b)i=ai−bi,{\displaystyle (\mathbf {a} -\mathbf {b} )_{i}=a_{i}-b_{i},}

aλ=(a1λ,a2λ,a3λ,…,anλ){\displaystyle {\frac {\mathbf {a} }{\lambda }}={\Big (}{\frac {a_{1}}{\lambda }},{\frac {a_{2}}{\lambda }},{\frac {a_{3}}{\lambda }},\dots ,{\frac {a_{n}}{\lambda }}{\Big )}},

или:

(aλ)i=aiλ.{\displaystyle {\Big (}{\frac {\mathbf {a} }{\lambda }}{\Big )}_{i}={\frac {a_{i}}{\lambda }}.}

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

Скалярное произведение:

a⋅b=a1b1+a2b2+a3b3+⋯+anbn{\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+\dots +a_{n}b_{n}},

или:

a⋅b=∑i=1naibi,{\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum \limits _{i=1}^{n}a_{i}b_{i},}

(Это справедливо только в прямоугольных координатах с единичным масштабом по всем осям).

Через скалярное произведение можно вычислить длину вектора

|a|=a⋅a{\displaystyle |\mathbf {a} |={\sqrt {\mathbf {a} \cdot \mathbf {a} }}}

и угол между векторами:

∠(a,b)=arccosa⋅b|a|⋅|b|{\displaystyle \angle {(\mathbf {a} ,\mathbf {b} )}=\mathrm {arccos} {\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\cdot |\mathbf {b} |}}}.

Внешнее произведение:

(a∧b)ij=aibj−ajbi{\displaystyle (\mathbf {a} \land \mathbf {b} )_{ij}=a_{i}b_{j}-a_{j}b_{i}},

для любой размерности пространства,

Векторное произведение (только для трехмерного же пространства, на котором оно и определено):

(a×b)x=aybz−azby{\displaystyle (\mathbf {a} \times \mathbf {b} )_{x}=a_{y}b_{z}-a_{z}b_{y}},

(a×b)y=azbx−axbz{\displaystyle (\mathbf {a} \times \mathbf {b} )_{y}=a_{z}b_{x}-a_{x}b_{z}},

(a×b)z=axby−aybx{\displaystyle (\mathbf {a} \times \mathbf {b} )_{z}=a_{x}b_{y}-a_{y}b_{x}}.

Это позволяет свести все операции над векторами к достаточно простым операциям над числами.

Нормальное уравнение плоскости – описание и пример.

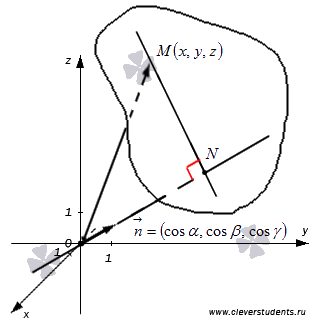
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz.

Рассмотрим плоскость, которая удалена на расстояние p () единиц от начала координат в положительном направлении нормального вектора плоскости . Будем считать, что длина вектора равна единице. Тогда его координаты равны направляющим косинусам, то есть, , причем . Обозначим расстояние от точки до плоскости как , то есть, точка N лежит на плоскости и длина отрезка ON равна p. Для наглядности отметим все данные на чертеже.

Получим уравнение этой плоскости.

Возьмем точку трехмерного пространства . Тогда ее радиус вектор имеет координаты , то есть, (при необходимости смотрите раздел ). Очевидно, что множество точек определяют описанную ранее плоскость тогда и только тогда, когда на направление вектора равна p, то есть, (смотрите рисунок ниже).

Тогда векторов и дает нам следующее равенство 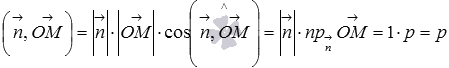. Это же представляется как . Сопоставление двух последних равенств дает нам искомое уравнение плоскости . Перенесем p в левую часть, и мы получим уравнение , которое называется нормальным уравнением плоскости или уравнением плоскости в нормальном виде. Нормальное уравнение плоскости иногда называют нормированным уравнением плоскости.

Итак, нормальное уравнение плоскости вида задает в прямоугольной системе координат Oxyz плоскость, удаленную от начала координат на расстояние p в положительном направлении единичного нормального вектора плоскости .

Следует заметить, что косинусы зачастую явно не фигурирует в нормальном уравнении плоскости, так как и — это некоторые действительные числа, сумма квадратов которых равна единице.

Приведем пример нормального уравнения плоскости.

Пусть плоскость задана в прямоугольной системе координат Oxyz уравнением в нормальном виде . Здесь , нормальный вектор плоскости имеет координаты , его длина равна единице, так как . Более того, заданная плоскость находится на расстоянии 7 единиц от начала координат в направлении вектора , так как p = 7.

Очевидно, что нормальное уравнение плоскости представляет собой общее уравнение плоскости вида , в котором числа A, B и C таковы, что длина нормального вектора плоскости равна единице, а число D неотрицательно.

Осталось разобраться с вопросом: «Как узнать, действительно ли перед нами нормальное уравнение плоскости»? Ответить на него достаточно просто: если выполняются оба условия и , то мы имеем уравнение плоскости в нормальном виде, если же хотя бы одно из условий не выполняется, то уравнение плоскости не является нормальным. Рассмотрим пример.

Пример.

Есть ли среди указанных уравнений уравнения плоскости в нормальном виде?

• ;
• ;
• .

Решение.

Начнем с первого уравнения. Проверим, равна ли длина нормального вектора плоскости единице. Вычислим длину: 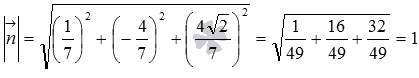. Осталось убедиться, что число p в этом уравнении положительно. Это действительно так, так как . Таким образом, первое уравнение плоскости является уравнением плоскости в нормальном виде.

Второе уравнение плоскости не является нормальным уравнением плоскости, так как не выполняется условие (в этом уравнении ).

В третьем уравнении длина нормального вектора не равна единице: 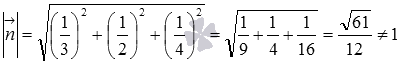. Поэтому оно не является уравнением плоскости в нормальном виде.

Ответ:

только первое уравнение является нормальным уравнением плоскости.

Вычисление поверхностного интеграла I рода

Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.

Разобьем поверхность S на части Обозначим через проекцию на плоскость Оху. При этом область D окажется разбитой на п частей Возьмем в произвольную точку и восстановим перпендикуляр к плоскости Оху до пересечения с поверхностью S . Получим точку на поверхности . Проведем в точке М, касательную плоскость и рассмотрим ту ее часть , которая на плоскость Оху проектируется в область (см. рис. 247). Площади элементарных частей обозначим как соответственно. Будем приближенно считать, что

Обозначив через, острый угол между осью Oz и нормалью п, к поверхности в точке получаем:

(область есть проекция на плоскость Оху).

Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке есть

где — координаты нормального вектора к плоскости. Острый угол уг есть угол между векторами и

Следовательно,

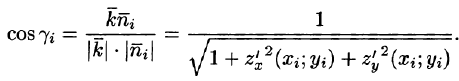
Равенство (57.4) принимает вид

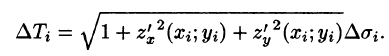
В правой части формулы (57.2) заменим (учитывая (57.3)) на полученное выражение для , a заменим на Поэтому, переходя к пределу при стремлении к нулю наибольшего диаметра (а следовательно, и ), получаем формулу

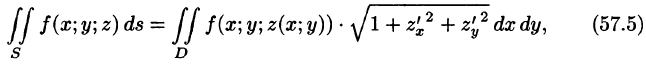
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.

Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:

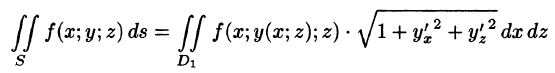
и

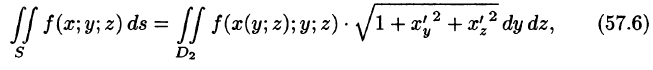
где — проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.

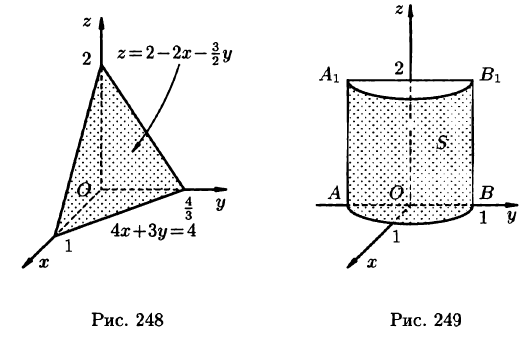
Пример:

Вычислить — часть плоскости расположенной в I октанте (см. рис. 248).

Решение:

Запишем уравнение плоскости в виде

Находим По формуле (57.5) имеем:

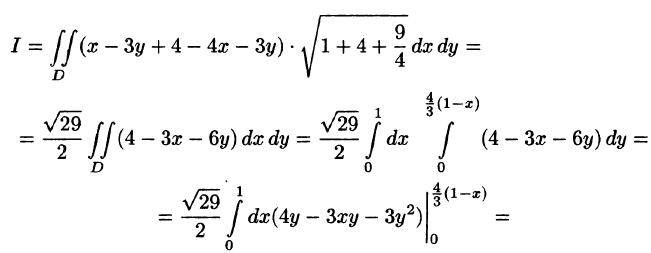
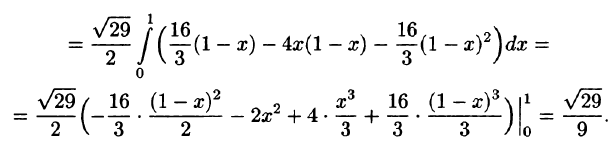
Пример:

Вычислить

где S — часть цилиндрической поверхности отсеченной плоскостями z = 0, z = 2 (см. рис. 249).

Решение:

Воспользуемся формулой (57.6). Поскольку

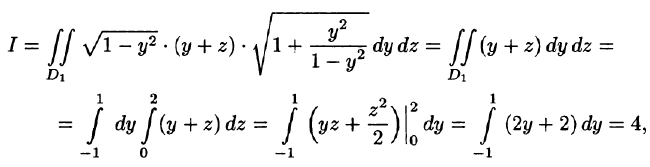
то где — прямоугольник

Площадь поверхности

Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле

или

Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы Все эти величины определяются одним и тем же способом: данную область разбивают на конечное число «мелких» частей, делая для каждой области деления упрощающие задачу предположения; находят приближенное значение искомой величины; переходят к пределу при неограниченном измельчении области деления. Проиллюстрируем описанный способ на примере определения массы материальной поверхности.

Масса поверхности

Пусть плотность распределения массы материальной поверхности есть Для нахождения массы поверхности:

1. Разбиваем поверхность S на п частей площадь которой обозначим .
2. Берем произвольную точку в каждой области . Предполагаем, что в пределах области плотность постоянна и равна значению ее в точке .
3. Масса области мало отличается от массы фиктивной однородной области с постоянной плотностью

4. Суммируя по всей области, получаем:

5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей , т. е.

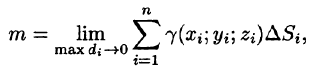
т. е.

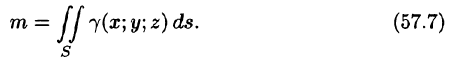
Моменты, центр тяжести поверхности

Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:

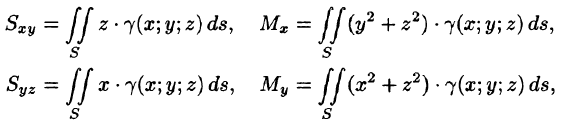
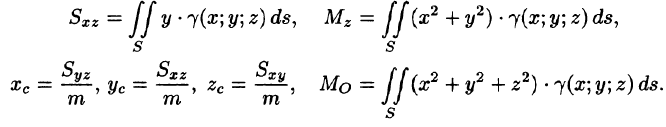
Пример:

Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение — поверхностная плотность полусферы.

По формуле (57.7) находим:

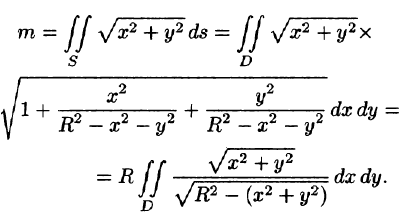
Переходим к полярным координатам:

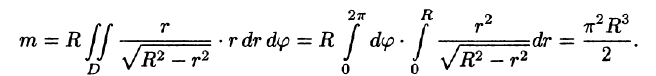
внутренний интеграл вычислен с помощью подстановки r= Rsint:

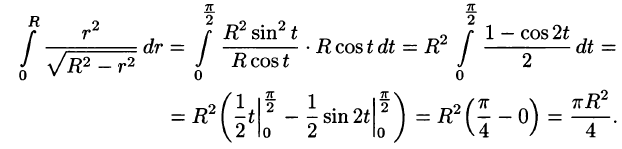
Поверхностный интеграл II рода

Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.

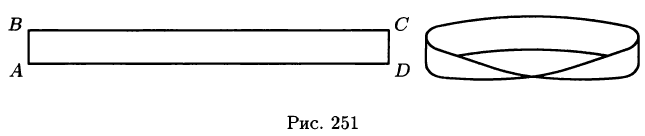
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), — функции, непрерывные в некоторой области D плоскости Оху и т.д.). После обхода такой поверхности, не пересекая ее границы, направление нормали к ней не меняется. Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точка А совмещается с точкой С, a В — с D (см. рис. 251).

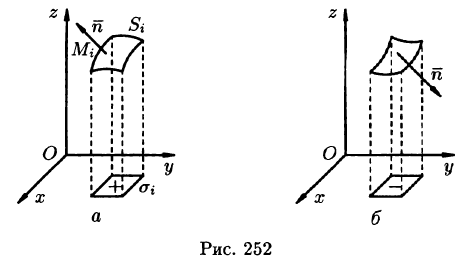
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части , где i = 1,2,…,п, и проектируем их на координатные плоскости. При этом площадь проекции берем со знаком «плюс», если выбрана верхняя сторона поверхности, или, что то же самое, если нормаль п к выбранной стороне поверхности составляет с осью Oz острый угол (см. рис. 252, а), т. е. со знаком «минус», если выбрана нижняя сторона поверхности (или ) (см. рис. 252, б). В этом случае интегральная сумма имеет вид

где — площадь проекции на плоскость Оху. Ее отличие от интегральной суммы (57.1) очевидно.

Предел интегральной суммы (58.1) при если он существует и не зависит от способа разбиения поверхности S на части и от выбора точек называется поверхностным интегралом II рода (по координатам) от функции f(x;y;z) по переменным x и у по выбранной стороне поверхности и обозначается

Итак

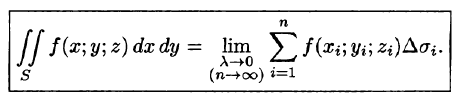
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:

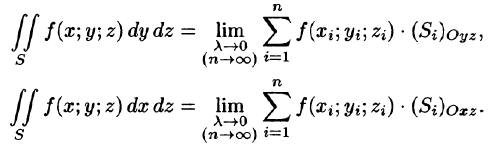
Общим видом поверхностного интеграла II рода служит интеграл

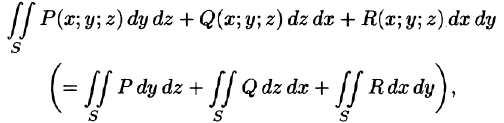
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.

Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается , по внутренней .

Из определения поверхностного интеграла II рода вытекают следующие его свойства:

1. Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
2. Постоянный множитель можно выносить за знак поверхностного интеграла.
3. Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
4. Поверхностный интеграл II рода по всей поверхности равен сумме интегралов по ее частям (аддитивное свойство), если пересекаются лишь по границе, их разделяющей.
5. Если — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то

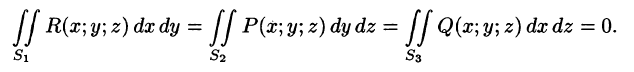
Историческая справка

Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.

Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь «декартовой».

Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.

Отличительные черты плоскости

Существует несколько отличительных качеств плоскости и ее параллельных линий:

•  Когда имеет линию (прямую) и она параллельна относительно другой, и пересекает ее, то полученная линия пересечения будет параллельна к исходной прямой.
• Если две пересекающиеся, проходят через параллельные прямые, то полученная линия пересечения будет также параллельна прямым.  
• Когда две плоскости параллельны, то у них нет точек для соприкосновения. 
• Когда две прямые пересечены в одной плоскости, но параллельны относительно 2 прямых линий из другой, значит эти плоскости также параллельны. 
• Если прямая перпендикулярна относительно заданной плоскости, то она будет перпендикулярна относительно любой линии на плоскости.
• Когда прямая перпендикулярна относительно 2-х пересекающихся прямых линий, которые лежат на плоскости, то она будет перпендикулярна к первой плоскости. 

Рассмотрим еще несколько свойств перпендикулярных к плоскости линий:

• Если прямая перпендикулярна относительно 1 из двух параллельно расположенных плоскостей, то она перпендикулярна и второй плоскости.
• Когда 1 из двух параллельных перпендикулярна данной плоскости, другая прямая также расположена перпендикулярна к исходной плоскости.
• Любая из прямых, пересекающих плоскость, когда она не является перпендикуляром, будет наклонной относительно заданной плоскости. 
• Когда любая плоскость перпендикулярна относительно прямой, значит она будет перпендикулярна и другой прямой.

Практическая часть

Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.

Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.

Пример 1

Имеем рисунок:

Рисунок 5. Отрезки на плоскости. Автор24 — интернет-биржа студенческих работ

На рисунке отрезки $AC, CD, DE, EB$ равны.

1. Серединой каких отрезков является точка $D$?
2. Какая точка является серединой отрезка $DB$?

Ответы:

1. точка $D$ является серединой отрезков $AB$ и $CE$;
2. точка $E$.

Рассмотрим другой простой пример, в котором нужно вычислить длину.

Пример 2

Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?

Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.

Ответ: 18 см.

Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.

Пример 3

Точка $B$ — середина отрезка $AC$. $AC = 8,4$ см. Какая длина $AB$?

Так как т. $B$ делит $AC$ пополам, то $AB = \frac{8,4}{2}$ см. Значит, $AB = 4,2$ см.

Ответ: 4,2 см.

Если в очередной задаче возникают трудности с пониманием её решения (например, нетипичные случаи с несколькими отрезками, образующими углами и прочими усложнениями), то лучше рассмотреть задачу, сделав по её условию рисунок. Наглядность способствует лучшему пониманию и более скорому нахождению решения.

Теперь решим задачи по аналитической геометрии.

Пример 4

Даны точки $T_1(7,11)$ и $T_2(1,23)$. Требуется найти координаты середины отрезка $T_1T_2$.

Абсцисса середины отрезка: $x=\frac{7+1}{2}=4$.
Ордината: $y=\frac{11+23}{2}=17$.

Ответ: $(4,17)$.

Пример 5

Даны точки $T(6,-1)$ и $S(-4,-8)$. Точка $S$ — середина $TK$. Найти координаты $K$.

Подставим значения и получим уравнения:

$-4=\frac{6+x_2}{2}, -8=\frac{-1+y_2}{2}.$

Найдём координаты:

$-2=6+x_2, -4=-1+y_2; x_2=-8, y_2=-3$.

Ответ: $K(-8,-3)$.

Неполное общее уравнение плоскости

Выше мы говорили о том, что, когда все числа А, B, C, D отличны от нуля, общее уравнение плоскости Ax+By+Cz+D=0 называютполным. В ином случае общее уравнение плоскости является неполным.

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

В случае, когда D = 0, мы получаем общее неполное уравнение плоскости: Ax+By+Cz+D=0⇔Ax+By+Cz=0

Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О (0, 0, 0), то придем к тождеству:

A·0+B·0+C·0=0⇔0≡0

• Если А = 0, В ≠ 0, С ≠ 0, или А ≠ 0, В = 0, С ≠0, или А ≠ 0, В ≠ 0, С = 0, то общие уравнения плоскостей имеют вид соответственно: By+Cz+D=0, или Ax+Cz+D=0, или Ax+By+D=0. Такие плоскости параллельны координатным осям Оx, Oy, Oz соответственно. Когда D=0, плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей By+Cz+D=0, Ax+Cz+D=0 и Ax+By+D=0 задают плоскости, которые перпендикулярны плоскостям Oyz, Oxz, Ozy соответственно.
• При А=0, В=0, С≠0, или А=0, В≠0, С=0, или А≠0, В=0, С=0 получим общие неполные уравнения плоскостей: Cz+D=0 ⇔z+DC=0⇔z=-DC⇔z=λ, λ∈R или By+D=0⇔y+DB=0⇔y=-DB⇔y=λ, λ∈R или Ax+D=0⇔x+DA=0⇔x=-DA⇔x=λ, λ∈R соответственно.

Эти уравнения определяют плоскости, которые параллельны координатным плоскостям Oxy, Oxz, Oyz соответственно и проходят через точки 0, 0, -DC, 0, -DB, 0 и -DA, 0, 0 соответственно. При D=0 уравнения самих координатных плоскостей Oxy, Oxz, Oyz выглядят так: z=0, y=0, x=0

соответственно.

Пример 4

Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М0(7, -2, 3). Необходимо составить общее уравнение заданной плоскости.

Р​​ешение

У​​​​​словием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz, а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0. Поскольку точка M0(7, -2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости  x+DA=0, иначе говоря, должно быть верным равенство  7+DA=0 . Преобразуем: DA=-7, тогда требуемое уравнение  имеет вид: x-7=0.

Задачу возможно решить еще одним способом.

Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости Oyz. Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости Oyz: i→=(1, 0, 0)

Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:

A(x-x0)+B(y-y0)+C(z-z0)=0⇔⇔1·(x-7)+0·(y+2)+0·(z-3)=0⇔⇔x-7=0

Ответ:x-7=0

Пример 5

Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М0(-3, 1, 2).

Решение

Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0). Условием задачи дано, что плоскость проходит через начало координат, тогда D=0 и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0.

Найдем значение BA. В исходных данных фигурирует точка М0(-3, 1, 2), координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: -3+BA·1=0, откуда определяем BA=3.

Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0.

Ответ: x+3y=0.

Что называют общим уравнением плоскости

Поговорим об уравнении плоскости для трехмерного пространства.

Плоскость в трехмерном пространстве

Разбираясь в чертежах, необходимо знать стандартные обозначения.

Все геометрические плоскости обычно прописывают прописными буквами греческого алфавита, а прямые обозначают большими буквами. Иногда для обозначения используют греческий алфавит, но с подстрочными индексами снизу. Чтобы изобразить ее, необходимо нарисовать параллелограмм, который создаст впечатление плоскости в пространстве.

Поскольку плоскость является бесконечной структурой, мы сможем отобразить лишь ее небольшой кусок. Поэтому вокруг параллелограмма изображают неровный овал, произвольной формы.

В реальности она могут быть расположены в любом произвольном порядке, иметь любой наклон или угол.

Если имеется прямоугольная система координат, расположенная в трехмерном пространстве, то в уравнении будут 3 неизвестных. Чтобы добиться равенства, нужно поставить в уравнение координаты точки, которая расположена именно в данной плоскости.

Если будут поставлены координаты другой точки, не из данной плоскости, тождество не получится.

Представим, что в 3-х мерном изображении и прям-ной координатной системы Oxyz общее уравнение, проходящей через две линии, имеет 3 неизвестных: x, yes и z. Они удовлетворяют координатам плоскости.

Значит, что при использовании этих данных для каждой из точек, лежащей на плоскости, обязательно должно получиться равенство. Если равенства нет, то точка к ней не относится.

Для записи общего уравнения через точку, необходимо вспомнить определение прямой линии, перпендикулярной заданной плоскости.  

Правило:

Каждая прямая будет перпендикулярной к плоскости, если она перпендикулярна относительно прямой, принадлежащей данной плоскости.
Это значит, что каждый нормальный вектор, соответствующий исходной плоскости, будет перпендикуляром к нулевому вектору, принадлежащему плоскости. Это является доказательством теоремы, которая будет определять вид общего уравнения плоскости.

Это значит, что каждый нормальный вектор, соответствующий исходной плоскости, будет перпендикуляром к нулевому вектору, принадлежащему плоскости. Это является доказательством теоремы, которая будет определять вид общего уравнения.

Примеры применения плоскости xoy

Плоскость xoy используется в различных областях науки и техники. Вот несколько примеров применения:

Область	Пример
Геометрия	Плоскость xoy является основной плоскостью для геометрических расчетов двумерных фигур, таких как треугольники, круги и квадраты. Она позволяет определить координаты точек на плоскости и выполнять различные геометрические операции, такие как вычисление длин, площадей и углов. Например, для построения треугольника на плоскости xoy можно использовать три точки с заданными координатами.
Физика	В физике плоскость xoy может использоваться для моделирования движения тел в двумерном пространстве. Например, при изучении броска предмета под углом к горизонту можно использовать координаты точек на плоскости xoy для определения траектории движения и вычисления времени полета, максимальной высоты или дальности полета.
Компьютерная графика	Плоскость xoy широко используется в компьютерной графике для отображения двумерных изображений и создания 2D-анимации. На плоскости xoy можно задать координаты объектов и выполнять различные трансформации, такие как повороты и масштабирование. Также на плоскости xoy можно задавать цвета и текстуры объектов.
Архитектура	При проектировании зданий и сооружений плоскость xoy может использоваться для отображения планов этажей. На плоскости xoy можно указать расположение стен, окон, дверей и других элементов здания. Также на основе плоскости xoy можно строить различные планы, например, планы санузлов, электрических систем или вентиляции.

Прямоугольная система координат в пространстве[править | править код]

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат OX{\displaystyle OX}, OY{\displaystyle OY} и OZ{\displaystyle OZ}. Оси координат пересекаются в точке O{\displaystyle O}, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. OX{\displaystyle OX} — ось абсцисс, OY{\displaystyle OY} — ось ординат, OZ{\displaystyle OZ} — ось аппликат.

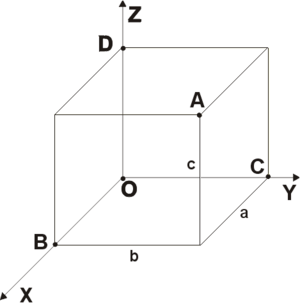
Рис. 2

Положение точки A{\displaystyle A} в пространстве определяется тремя координатами x{\displaystyle x}, y{\displaystyle y} и z{\displaystyle z}. Координата x{\displaystyle x} равна длине отрезка OB{\displaystyle OB}, координата y{\displaystyle y} — длине отрезка OC{\displaystyle OC}, координата z{\displaystyle z} — длине отрезка OD{\displaystyle OD} в выбранных единицах измерения. Отрезки OB{\displaystyle OB}, OC{\displaystyle OC} и OD{\displaystyle OD} определяются плоскостями, проведёнными из точки A{\displaystyle A} параллельно плоскостям YOZ{\displaystyle YOZ}, XOZ{\displaystyle XOZ} и XOY{\displaystyle XOY} соответственно.

Координата x{\displaystyle x} называется абсциссой точки A{\displaystyle A},

координата y{\displaystyle y} — ординатой точки A{\displaystyle A},

координата z{\displaystyle z} — аппликата (лат. applicata — прилегающая) точки A{\displaystyle A}.

Символически это записывают так:

A(x,y,z){\displaystyle A(x,\;y,\;z)},

или

A=(x,y,z){\displaystyle A=(x,\;y,\;z)},

или привязывают запись координат к конкретной точке с помощью индекса:

xA,yA,zA{\displaystyle x_{A},\;y_{A},\;z_{A}},

и т. п.

Каждая ось рассматривается как числовая прямая, то есть имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка B{\displaystyle B} лежала не как на рисунке — на луче OX{\displaystyle OX}, а на его продолжении в обратную сторону от точки O{\displaystyle O} (на отрицательной части оси OX{\displaystyle OX}), то абсцисса x{\displaystyle x} точки A{\displaystyle A} была бы отрицательной (минус расстоянию OB{\displaystyle OB}). Аналогично и для двух других осей.

Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении ещё и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси OX{\displaystyle OX} против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY{\displaystyle OY}, если этот поворот наблюдать со стороны положительного направления оси OZ{\displaystyle OZ}).

Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями, называется октантом.

Общее уравнение плоскости, проходящей через точку

Повторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество.

Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости.

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0

Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости.

Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение:

2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0

Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости.

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.

В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости.

Решение

Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так:

λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.

Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0

Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) .

Возможно получить это уравнение другим способом.

Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:

n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости.

Решение

Рассмотрим два способа решения.

1. Исходные условия позволяют получить следующие данные:

x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5

Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0

3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0

1. Допустим, М ( x , y , z ) – некоторая точки заданной плоскости. Определим координаты вектора M 0 M → по координатам точек начала и конца:

M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 )

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0

Ответ: 3 x + 7 y — 5 z — 26 = 0

Применение плоскости xoy в графике и дизайне

В графике плоскость xoy используется для построения двумерных графиков функций. На плоскости xoy можно отобразить зависимость одной переменной от другой, создавая линии и кривые, которые позволяют визуализировать математические и физические законы, статистические данные и тренды.

В дизайне плоскость xoy применяется для создания двумерных композиций и макетов. На плоскости xoy можно размещать и располагать элементы изображения, текстовые блоки, иллюстрации и другие объекты. Это позволяет дизайнерам управлять пространством и композицией, создавать баланс и гармонию между элементами.

Примеры использования плоскости xoy в графике и дизайне:

1. Графики функций: Плоскость xoy используется для построения линейных, криволинейных и других видов графиков функций, что позволяет анализировать и представлять зависимость переменных.

2. Дизайн интерфейсов: Плоскость xoy помогает размещать элементы интерфейса на экране, учитывая их взаимное расположение и связи, создавая удобство и логическую структуру дизайна.

3. Оформление печатных изданий: Плоскость xoy используется для компоновки и расположения текстовых и графических элементов в макетах журналов, книг, рекламных материалов и других печатных продуктов.

4. Создание логотипов и иллюстраций: Плоскость xoy позволяет дизайнерам создавать уникальные логотипы и иллюстрации с использованием различных форм, линий и текстур.

Использование плоскости xoy в графике и дизайне помогает визуализировать информацию, создавать эстетически привлекательные композиции и облегчает восприятие пользователем.