Взаимно простые числа

Проблема обобщения в процессе обучения математике в школе

В программно-методических материалах по математике в качестве одной из основных целей математического образования названо интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценной жизни в обществе.

Пониманием роли мыслительного процесса как внутреннего условия, опосредующего любые виды внешних воздействий (в том числе — учебных), было продиктовано решение вопроса о составе и структуре умственных способностей. Так С. Л. Рубинштейн полагал, что «ядром» или общим, главным компонентом любой умственной способности является свойственное данному человеку качество процессов анализа, синтеза и обобщения. Особую роль при этом играет обобщение отношений между понятиями в том или ином предметном материале (включая, разумеется, и материал школьного курса математики).

Таким образом, по мнению С. Л. Рубинштейна, индивидуальный интеллект складывается по мере того, как образуются, генерализируются и закреп 14 ляются основные мыслительные операции: анализ, синтез, обобщение, классификация и т. д. Вторым, производным компонентом способностей он считал более или менее слаженную и отработанную совокупность этих операций. Так что суть интеллектуального воспитания личности заключается в формировании культуры тех внутренних процессов, которые лежат в основе способности к постоянному возникновению у человека новых мыслей, что служит самым очевидным критерием уровня интеллектуального развития.

По определению Ж. Пиаже , интеллект — это наиболее совершенная форма адаптации организма к среде, представляющая собой единство процесса ассимиляции (то есть воспроизведения элементов среды в психике субъекта в виде когнитивных психических схем) и процесса аккомодации (то есть изменения этих когнитивных схем в зависимости от требований объективного мира). Таким образом, суть интеллекта, по Ж. Пиаже, заключается в возможности осуществлять гибкое и одновременно устойчивое приспособление к физической и социальной действительности, а его основное назначение состоит в структурировании (организации) взаимодействия человека со средой.

По мнению Ж. Пиаже, развитие интеллекта представляет собой стихийный, подчинённый своим особым законам процесс вызревания операциональных структур (схем), постепенно вырастающих из предметно-житейского опыта ребенка. Следовательно, интеллектуальное развитие есть развитие именно операциональных структур интеллекта. В ходе этого развития мыслительные операции постепенно приобретают качественно новые свойства: скоординиро-ванность (то есть взаимосвязанность и согласованность множества операций), обратимость (то есть возможность в любой момент вернуться к начальной точке своих рассуждений, перейти к рассмотрению объекта с прямо противоположной точки зрения), автоматизированность (то есть непроизвольность применения), сокращённое (то есть невыявленность отдельных звеньев).

Благодаря сформированности мыслительных операций оказывается возможной полноценная интеллектуальная адаптация подростка к происходящему. Наиболее яркой иллюстрацией подобной формы адаптации, по мнению Ж. Пиаже, является именно математическое творчество.

X. Вернер полагал, что своеобразие высшего уровня умственного развития заключается в появлении межфункциональных связей и субординации низших уровней познавательной активности по отношению к высшим. Все эти процессы определяются работой «обобщающего мышления», которое и является психологической основой эффективных знаний о мире.

Натуральные числа. Множество натуральных чисел

Натуральные числа $1, 2, 3, \dots$ используются для счёта (одна груша, две груши, три груши и т.д.) или для указания порядкового номера предмета среди ему подобных.

Натуральные числа принято записывать с помощью арабских цифр: $0, 1, 2, 3, 4, 5, 6, 7, 8, 9$.

Рисунок 1.

Определение 1

Натуральные числа (или естественные числа) — числа, которые возникают естественным образом при подсчете чего-либо.

Пример 1

Натуральными будут числа: $3, 48, 157, 1089, 25556$.

Если выстроить все натуральные числа в порядке их возрастания, то получим натуральный ряд.

Для определения натуральных чисел существует два подхода:

1. Числа, которые возникают при подсчете (нумерации) предметов (например, первый, второй и т.д.).

2. Числа, которые используют для обозначения количества предметов (нет стула, один стул, два стула и т.д.).

При первом подходе натуральный ряд начинается с единицы, при втором — с нуля.

Математики не пришли к единому выводу считать ли ноль натуральным числом. В большинстве российских источников традиционным является первый подход. Второй подход широко используется в программировании (например, при индексации массивов, нумерации битов машинного кода и т.д.).

Замечание 2

К натуральным числам не относятся ни отрицательные, ни нецелые числа.

Определение 2

Множество всех натуральных чисел обозначается $N=\left\{1,\ 2,\ 3,\ 4,\ \dots ,\ n,\ \dots \right\}$ и характеризуется своей бесконечностью, т.к. для любого натурального числа $n$ существует натуральное число, которое будет большее $n$.

Пример 2

Какие из чисел являются натуральными?

\{5};\ \ 38;\ \ \ -38;\ \ 12,5;\ \ 4.\]

Ответ: $5;\ \ 38;\ \ \ 4.$

При формулировке и доказательстве многих теорем арифметики натуральных чисел удобно использовать и ноль, поэтому при первом подходе применяется понятие расширенного множества натуральных чисел, которое содержит ноль и обозначается $N_0$ или $Z_0$.

Задачи на построение натурального ряда

Задача 1. Постройте натуральный ряд, который начинается с числа 3 и каждое последующее число больше предыдущего на 5. Найдите 10-е число в этом ряду.

Решение: Исходный натуральный ряд: 3, 8, 13, 18, 23, 28, 33, 38, 43, 48, … Для нахождения 10-го числа прибавим к 3 число 9 умноженное на 5: 3 + 9 x 5 = 48.

Задача 2. Постройте натуральный ряд, который начинается с 1 и каждое последующее число равно сумме двух предыдущих чисел. Найдите 8-е число в этом ряду.

Решение: Исходный натуральный ряд: 1, 1, 2, 3, 5, 8, 13, 21, 34, … Для нахождения 8-го числа, нужно сложить 5 и 3: 5 + 3 = 8.

Задача 3. Постройте натуральный ряд, который начинается с 2 и каждое последующее число равно произведению предыдущего числа на 3. Найдите 6-е число в этом ряду.

Решение: Исходный натуральный ряд: 2, 6, 18, 54, 162, … Для нахождения 6-го числа, нужно умножить предыдущее число на 3: 162 x 3 = 486.

Сочетания с повторениями: примеры

Примеры сочетаний с повторениями могут быть полезны в различных областях, таких как математика, информатика, статистика и другие. Рассмотрим несколько примеров:

Пример	Объекты	Результат
Сочетания с повторениями из 2 элементов из множества {‘A’, ‘B’, ‘C’}	А, А; А, В; А, С; В, В; В, С; С, С	AA, AB, AC, BB, BC, CC
Сочетания с повторениями из 3 элементов из множества {‘1’, ‘2’}	1, 1, 1; 1, 1, 2; 1, 2, 2; 2, 2, 2	111, 112, 122, 222
Сочетания с повторениями из 4 элементов из множества {‘X’, ‘Y’, ‘Z’}	X, X, X, Y; X, X, X, Z; X, X, Y, Y; X, X, Y, Z; X, X, Z, Z; X, Y, Y, Y; X, Y, Y, Z; X, Y, Z, Z; X, Z, Z, Z; Y, Y, Y, Y; Y, Y, Y, Z; Y, Y, Z, Z; Y, Z, Z, Z; Z, Z, Z, Z	XXXY, XXXZ, XXYY, XXYZ, XXZZ, XYYY, XYYZ, XYZZ, XZZZ, YYYY, YYYZ, YYZZ, YZZZ, ZZZZ

Как можно видеть из примеров, сочетания с повторениями позволяют получать различные комбинации из заданных элементов. Этот инструмент широко используется при решении задач, связанных с перебором, комбинаторикой и вероятностными расчетами.

Ноль как натуральное число

В русской литературе принято исключать нуль из числа натуральных чисел ($0\notin N$), а множество натуральных чисел с нулём обозначают $N_0$.

В международной математической литературе множество $\left\{1,\ \ 2,\ \ 3,\ \dots \right\}$ принято называть множеством положительных целых чисел и обозначать $Z+$. Множество $\left\{0,\ \ 1,\ \ 2,\ \dots \right\}$ принято называть множеством неотрицательных целых чисел и обозначать $Z{\ge 0}$.

Чтобы прочитать натуральное число, нужно выполнить следующие действия:

1. Разбить число справа налево на группы из $3$ цифр.

2. Прочитать слева направо по очереди группы из $3$ цифр и добавить название класса.

3. Название класса пропускают, если в группе цифр все нули.

Рисунок 2.

Каждую цифру класса называют разрядом класса.

Меньшим натуральным числом является то, которое при проведении подсчета используется раньше. Например, число $9$ меньше $20$ (записывается $9 55$.

Геометрический алгоритм Евклида

Данный алгоритм часто применяется для решения задач по нахождению наибольшего общего делителя двух чисел (целых). Алгоритм работает следующим образом:

Возьмем 2 целых числа и обозначим их как a и b. Представим числа в виде отрезков. Каждый из них имеет свое числовое значение.

• Из большего отрезка нужно вычесть меньший;
• Больший отрезок заменим полученной разностью величин;
• Продолжаем вычитать из большего отрезка меньший, пока они не станут равны;
• Процедуру вычитания проводим до тех пор, пока отрезки не станут равны.

Если в итоге получаем отрезки равной величины, то значит, что они соизмеримы. И последний полученный результат — это и есть показатель их наибольшей общей меры.

Если общей меры отрезков нет, то процесс будет продолжаться бесконечно.

Метод использования алгоритма Евклида. Найдем НОД двух чисел 1071 и 462. Представим и в виде буквенных обозначений. Пусть, a = 1071, b = 462.

Из 1071 вычтем 462 кратное число раз. Это можно сделать 2 раза. Количество раз, которое можно вычесть наименьшее число из большего обозначим буквой q.

1071 – 462 ⋅ 2 = 147

Из наименьшей величины (все, как в алгоритме Евклида) вычтем кратное число раз разность.

462 – 174 ⋅ 3 = 21

И снова проделываем аналогичное вычисление.

147 – 21 ⋅ 7 = 0

Последний остаток в данном примере = 21. Следовательно, НОД для чисел 1071 и 462 =21.  Делаем вывод, что 21 > 1, значит данные числа не будут взаимно простыми.

Теперь можно попробовать применить данную формулу на практике.

Пример

Условие: нужно выяснить, являются ли числа 275 и 84 взаимно простыми или нет.

И то, и то число, точно имеют больше 1 делителя. Сразу сказать, что они взаимно простые нельзя. Для вычисления НОД применим алгоритм Евклида:

275 = 84 ⋅ 3 + 23 , 84 = 23 ⋅ 3 + 15 , 23 = 15 ⋅ 1 + 8 , 15 = 8 ⋅ 1 + 7 , 8 = 7 ⋅ 1 + 1 , 7 = 7 ⋅ 1

Ответ: Так как, НОД чисел 84 и 275 равен 1, то взаимная простота чисел доказана.

Если есть числовой ряд с большим количеством чисел и у всех у них наибольшим делителем является единица, то они будут проявлять свойство взаимной простоты по отношению друг к другу.

Количество чисел не имеет значение. Их может быть сколько угодно много. Главное – наибольший общий делитель – единица. Для наглядности, возьмем ряд чисел: 2, 3, 11, 19, 667. Они все делятся только сами на себя и на 1. Из это следует, что их свойство взаимной простоты доказано.

Примеры

Условие: определить наличие взаимной простоты у чисел 331, 463, 733 или опровергнуть ее.

Решение:

Используем для решения таблицу простых чисел. Проверим данные числа и таблицу. Да, в таблице можно встретить
их все. Это значит, что общим делителем чисел будет 1.

Ответ: все числа находятся в таблице простых чисел. Их наибольший делить -1. Значит все они взаимно
простые друг к другу.

Докажите, что следующие числа не являются взаимно простыми (105, — 14, — 2007, — 91).

Решение:

• Нужно найти общий наибольший делитель. Это можно сделать любым удобным способом;
• Вспоминаем, что отрицательные числа имеют те же делители, что и положительные.
• НОД для всех чисел будет = 7.

Ответ: 7 больше 1. Значит, что числа не будут являться взаимно простыми.

Иррациональные и действительные числа

Долгое время дробей было достаточно человечеству для любых расчетов. Древние греки полагали, что любое отношение величин, которое может встретиться в реальном мире, будет выражаться какой-нибудь дробью. Однако это не так. Один из учеников Пифагора, Гиппас, пытался найти соотношение между стороной квадрата и его диагональю. В результате он осознал, что такой дроби просто не существует.

Это соотношение равно квадратному корню из 2 (что доказывается в курсе геометрии), которое обозначается как . Это такое число, которое при умножении на само себя дает 2. Докажем, что оно не может быть выражено несократимой дробью.

При этом она равна дроби 2/1. Следовательно, b*b = 1 , а a*a = 2. Однако не существует такого натурального числа a, которое при умножении на себя дает 2. Получается противоречие, значит,  нельзя представить в виде дроби. Математики говорят, что  является иррациональным числом. Аналогичным образом можно доказать иррациональность квадратного корня из любого натурального числа, не являющимся квадратом другого натурального числа.

Исторически именно  был первым иррациональным числом, открытым человечеством. Его значение примерно равно 1,414213562. Способы его вычисления будут освещены позже. Заметим лишь, что у этого числа нельзя найти периода в его десятичной записи.

Вообще любое иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби. Это значит, что в числах после запятой не будет никакого периода. Чуть раньше мы уже приводили два примера иррациональных чисел:

• 0,12345678910111213141516…;
• 0,10100100010001000001….

Ещё одним иррациональным числом является π, которое равно отношению длины окружности к ее диаметру и примерно равно 3,1415926…

Для обозначения множества иррациональных чисел используется буква I.

Рациональные и иррациональные числа вместе образуют множество действительных чисел, обозначаемое буквой R. Иногда их также называют вещественными числами.

Слово «вещественное» указывает на физический смысл этого понятия. Любой результат измерения какой-либо величины (длины, площади, объема, массы и т. д.) является вещественным числом.

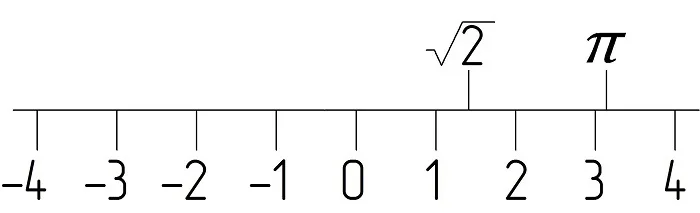
Важно, что на числовой прямой, или координатной оси, каждой точке в соответствие можно поставить действительное число, и наоборот, каждому действительному числу соответствует единственная точка на числовой прямой. В качестве примера показаны числа π и  на числовой прямой:

Таким образом, можно составить следующую классификацию чисел, используемых в математике:

Все числа, которые встретятся в ходе изучения школьной программы математики и других наук, будут действительными. Однако стоит отметить, что в высшей математике, изучаемой в университете, будут изучаться и более сложные объекты, называемые комплексными числами.

Как определить, что числа попарно различны?

Чтобы определить, что числа попарно различны, нужно проверить, что все числа в наборе не повторяются и не совпадают друг с другом.

Для этого необходимо выполнить следующие действия:

1. Составить набор чисел: выберите любое количество чисел, которые хотите проверить на попарную различность.
2. Проверить наличие повторений: просмотрите весь набор и убедитесь, что каждое число встречается только один раз. Если в наборе есть повторяющиеся числа, то они не являются попарно различными.
3. Сравнить все числа друг с другом: сравните каждое число в наборе со всеми остальными числами. Если хотя бы одно число совпадает с другим числом, то набор не является попарно различным.

Попарно различные числа означают, что каждое число в наборе отличается от всех остальных чисел и не повторяется. Наличие повторений или совпадений в наборе делает его неподходящим для условия попарной различности.

Проверяя числа на попарную различность, можно убедиться, что все числа в наборе действительно уникальны и не совпадают друг с другом. Это может быть полезным при решении определенных математических или программных задач, где требуется работать с наборами попарно различных чисел.

Критерии попарной различности

Для определения попарной различности чисел необходимо выполнение нескольких критериев:

1. Каждое число должно быть уникальным и не повторяться среди остальных чисел.
2. Попарно различные числа не могут иметь никаких общих элементов или свойств. Если два числа имеют хотя бы одно общее свойство, они не являются попарно различными.
3. Попарно различные числа должны быть различными на всех уровнях сравнения. Например, если есть два числа, то необходимо проверить их различие как в целом, так и в отдельных разрядах или десятичных позициях.

Таким образом, попарно различные числа могут быть определены только при выполнении указанных критериев. Их соблюдение позволяет гарантировать факт полного отсутствия любого сходства или повторения между числами.

Применение алгоритмов для определения попарной различности чисел

Для определения попарной различности чисел можно применять различные алгоритмы. Один из простых способов — это использование двойного цикла. Перебираются все пары чисел из заданного множества, и проверяется, что оба числа различны:

В этом алгоритме каждая пара чисел проверяется только один раз, поэтому он имеет временную сложность O(n^2), где n — количество чисел в множестве. Если количество чисел велико, то этот алгоритм может быть неэффективным.

Еще одним эффективным алгоритмом может являться использование структуры данных Set. Set — это коллекция уникальных значений, и добавление элемента в Set не происходит, если такое значение уже существует. Для определения попарной различности чисел можно добавить все числа из заданного множества в Set и затем проверить, что размер Set равен размеру множества чисел:

В этом алгоритме используется один проход по всем числам, и добавление числа в Set происходит за константное время O(1). Таким образом, алгоритм имеет временную сложность O(n), где n — количество чисел в множестве.

Выбор алгоритма для определения попарной различности чисел зависит от конкретной задачи и требований к производительности. При работе с небольшими множествами чисел можно использовать более простые алгоритмы, а при работе с большими множествами лучше выбрать более эффективные алгоритмы.

Операции над натуральными числами

К операциям над натуральными числами относят:

1. Сложение: a+b=c, где

a, b — слагаемые, c — сумма.

Сумма всегда больше любого из слагаемых.

Когда нужно найти неизвестное слагаемое, из суммы вычитают известное слагаемое: b=c-a.

1. Умножение: a*b=c, где

a, b — множители или множитель и сомножитель, c — их произведение.

В операции умножения натуральных чисел самым большим числом будет произведение.

Чтобы найти неизвестный множитель, произведение делят на известный множитель: b=c:a.

1. Вычитание: a-b=c, где

a — уменьшаемое, b — вычитаемое, c — разность.

Самое большое число в операции вычитания — уменьшаемое.

Почему попарная разность чисел важна?

Попарная разность чисел — это разность между каждыми двумя числами в наборе. Использование попарных разностей может быть полезным во многих аспектах, и вот почему:

1. Анализ данных: Попарные разности чисел могут быть использованы для анализа данных и выявления интересных закономерностей. Например, попарные разности могут помочь обнаружить тренды или изменения в данных.
2. Поиск аномалий: Сравнение попарных разностей чисел может помочь выявить аномалии или выбросы, которые могут быть важными для анализа или принятия решений. Например, если попарная разность между двумя числами значительно отличается от остальных разностей, это может указывать на необычное событие или причину.
3. Прогнозирование: Попарные разности чисел могут быть использованы для прогнозирования будущих значений. Например, если попарная разность чисел показывает постепенное увеличение, это может указывать на то, что значения будут продолжать расти в будущем.
4. Сравнение и ранжирование: Попарные разности чисел могут быть использованы для сравнения и ранжирования различных наборов данных. Например, сравнение попарных разностей между двумя наборами чисел может помочь определить, в каком наборе чисел различия более значительны.
5. Оптимизация: Попарные разности чисел могут быть использованы для оптимизации процессов или конкретных значений. Например, если попарная разность чисел указывает на то, что одно значение является более эффективным или оптимальным, это может помочь принять соответствующие решения.

Все эти преимущества делают попарные разности чисел важными инструментами для анализа данных, прогнозирования и принятия решений. Они позволяют нам получить более глубокое понимание данных и использовать их в нашу пользу.

Что такое попарно различные числа?

Для определения попарной различности чисел необходимо проверить каждую пару чисел в наборе и убедиться, что они не равны друг другу. Если в наборе нет двух чисел, которые совпадают, можно сказать, что числа в наборе попарно различны.

Например, набор чисел {2, 4, 6, 8} является попарно различным, потому что ни одна пара чисел в наборе не равна друг другу. Однако набор чисел {1, 2, 3, 1} не является попарно различным, потому что первое и последнее числа равны.

Попарная различность чисел имеет важное значение в различных областях математики и информатики, например, при проверке уникальности элементов в наборе или при поиске дубликатов

Разнообразие чисел

Уникальность чисел обеспечивается тем, что каждое из них имеет свою собственную, неповторимую комбинацию цифр. Например, числа 123 и 321 считаются различными, так как имеют разную последовательность цифр.

Уникальные числа могут быть использованы для решения различных задач и построения разнообразных моделей. Например, они могут быть использованы для создания уникальных идентификаторов элементов в базе данных или для генерации случайных чисел в программировании.

Попарно различные числа часто используются для представления данных в таблицах. Таблица является удобным и наглядным способом представления разнообразных числовых значений. Она может содержать столбцы и строки, в которых числа могут быть упорядочены или группируются в соответствии с определенными правилами.

Например, таблица может содержать данные о населении различных городов или о стоимости различных товаров. Попарно различные числа позволяют уникально идентифицировать каждый элемент данных в таблице и облегчают поиск и обработку информации.

Название	Город	Население
Москва	Москва	12 678 079
Санкт-Петербург	Санкт-Петербург	5 383 890
Новосибирск	Новосибирск	1 663 100

В таблице выше приведены примеры данных о населении различных городов. Каждая ячейка таблицы содержит попарно различное число, которое уникально идентифицирует соответствующую информацию.

Использование попарно различных чисел позволяет создавать точное и структурированное представление данных, что делает их понятными и легко анализируемыми. Они полезны не только в математике и программировании, но и во многих других областях, где требуется работа с числовыми данными.

Свойства попарно различных чисел

Свойства попарно различных чисел соответствуют их определению:

Свойство	Описание
Уникальность	Каждое число в наборе попарно различных чисел встречается только один раз.
Неповторимость	Никакие два числа в наборе попарно различных чисел не совпадают.
Разнообразие	Набор попарно различных чисел содержит различные значения, что делает его интересным для исследования и применений в различных областях.

Свойства попарно различных чисел являются важными при решении различных задач, в том числе в комбинаторике, теории множеств, алгоритмах и других областях математики и информатики. Представление чисел как попарно различных наборов позволяет облегчить анализ и манипуляции с ними.

Как находить пропущенные числа в натуральном ряду

Натуральный ряд чисел — это последовательность натуральных чисел, начинающаяся с 1 и без конечной границы. Нередко в натуральном ряду могут быть пропущены числа, и нам нужно их найти.

Самый простой способ для нахождения пропущенных чисел — это пройти по всему ряду, начиная с 1, и проверять, есть ли каждое следующее число в последовательности. Если число пропущено, отмечаем это и продолжаем проверять дальше. Например:

1. Начинаем с 1 — все нормально.
2. Проверяем 2 — все нормально.
3. Проверяем 3 — ой, 3 пропущено!
4. Проверяем 4 — все нормально.
5. Проверяем 5 — все нормально.
6. И так далее…

Если последовательность очень длинная, то этот метод может оказаться довольно трудоемким. В этом случае можно воспользоваться формулой для суммы элементов арифметической прогрессии:

Здесь Sn — сумма первых n элементов прогрессии; a1 — первый элемент прогрессии; an — последний элемент прогрессии; n — количество элементов в прогрессии.

Найдем, например, пропущенное число в прогрессии 1, 2, 4, 5, 6:

Первый элемент a1 = 1, последний элемент an = 6, количество элементов n = 5. Тогда сумма элементов равна:

Так как стандартный натуральный ряд чисел не может содержать дробных чисел, то мы можем сделать вывод, что число 3 пропущено:

1. 1, 2
2. отсутствует 3
3. 4
4. 5
5. 6

Используя эту формулу, можно находить пропущенные числа в любом натуральном ряду, где не более чем одно число пропущено.

Что такое взаимно простые числа?

Определение

Взаимно простым числом называют целое число, которое имеет с другим числом наибольший общий делитель – 1 (единицу).

Возьмем 2 простых числа и определим их, как a и b. Взаимно простыми будут те числа, которые имеют 1, как наибольший общий делитель (НОД). (a, b) = 1

У двух взаимно простых чисел будет один положительный общий делитель. И делитель будет равен 1. Только два таких числа имеют два общих делителя 1 и -1.

Пример 1:

Простым примером взаимно простых будут числа 5 и 11. Почему? Давайте посмотрим на делители этих чисел: 5 делится на 5 и на 1, а число 11 можно разделить на 11 и на 1 (без остатка). Общим положительным делителем этих двух чисел будет единица. Единица – самый большой общий делитель двух чисел – значит, что они будут взаимно простые.

Но не только простые числа могут быть взаимно простыми по отношению друг к другу. Условие взаимной простоты образуется и между составными числами.

Определение

Составное число – число, делители которого отличаются от самого числа и единицы).

Ситуаций, где в паре чисел одно является простым, а второе составным, или оба являются составными – не редкость. И мы научимся с ними работать.

Пример 2:

Возьмем для примера два числа: -9 и 8. Мы утверждаем, что они образуют взаимно простую пару. Так ли это? Давайте проверим. Для того, чтобы это доказать (или опровергнуть) нужно найти их общий делитель. Распишем делители каждого из чисел в ряд:

Для числа 8 делителями будут: ±1, ±2, ±4, ±8;Для числа 9 делителями будут: ±1, ±3, ±9.

Выбираем из рядов делителей общий и самый большой: ±1. Из этого следует, что, если наибольший общий делитель (НОД) чисел 8 и -9 это единица, то они взаимно простые друг к другу.

А вот числа 45 и 500 не будут таковыми. Почему? Помимо единицы, они имеют еще один общий делитель 5, и он больше единицы (вспоминаем правило про наибольший общий делитель). 5 больше 1, значит о взаимной простоте чисел не может быть и речи.

Аналогичная ситуация с числами 201 и 3. Если расписать все из общие делители, то там будет число 3. А 3 больше 1, значит и в этой ситуации нет взаимной простоты между числами.

Как показывает практика, решение задач на определение взаимной простоты встречаются часто и не только в школьных учебниках. Вся их суть сводится к одному: поиск наибольшего общего делителя этих чисел и сравнение его с единицей.  Расписывать все делители будет очень проблематично, в некоторых случаях. Например, число 234 567. Для упрощения задачи есть несколько вариантов:

• Использование таблицы простых чисел. Если одно из чисел в ней есть, то оно простое и делится на себя и единицу;
• Алгоритм Евклида.

Разберем решение таковой задачи на примере.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Организация и основные итоги эксперимента

Первая часть эксперимента была начата в 1996 году. Здесь преследовалась цель определения критериев отбора учебного материала и принципов его преподавания в классах с углубленным изучением математики или для школьников, интересующихся математикой и связывающих свою дальнейшую учебу с математическим циклом дисциплин.

Для сбора и анализа данных по проблеме исследования проводился устный и письменный опрос учителей г. Краснодара и Краснодарского края (в плане сотрудничества с Краснодарским экспериментальным центром развития образования), преподающих в классах с углубленным изучением математики или работающих с одаренными школьниками в рамках факультативных занятий, подготовки к олимпиадам, участвующих в проведении летних математических школ Краснодарского края.

Учителям предлагали следующие вопросы:

1. В каком виде (ретроспективно или обобщая) вы проводите повторение тем школьного курса математики, связанных с понятием «число»?

2. Повторяя принцип позиционной записи числа, рассматриваете ли Вы прием дробления записи числа в десятичной системе счисления на блоки цифр (по п цифр в каждом блоке)?

3

Акцентируете ли Вы внимание на разнице в понятиях «число» и «цифра»?. 4

Решаете ли Вы с учащимися задачи на применение основной теоремы арифметики (анализ сомножителей, понятие простого и составного числа)?

4. Решаете ли Вы с учащимися задачи на применение основной теоремы арифметики (анализ сомножителей, понятие простого и составного числа)?

5. В какой форме Вы доказываете признаки делимости (как достаточные или необходимые и достаточные признаки)?

6

Повторяя схему деления с остатком на фиксированное число, обращаете ли Вы внимание на оценку остатка и, в связи с этим — на диапазон выбора остатков для данного делителя?. 7

Рассматривая признак делимости на данное число, выделяете ли Вы объект, который несет информацию об остатке (понятие равноостаточных чисел)?

7. Рассматривая признак делимости на данное число, выделяете ли Вы объект, который несет информацию об остатке (понятие равноостаточных чисел)?

8. Используете ли Вы метод работы с классами равноостаточных чисел (операции над классами)?

9. Обсуждаете ли Вы с учащимися принцип расширения числовых множеств?

10.Проводите ли Вы сравнение наборов свойств операций для различных числовых множеств с введенными на них операциями (например, в виде классификационных таблиц)? Если да, то используете ли Вы термины «группа», «кольцо», «поле»?

11.В случае положительного ответа на вопрос 10: рассматриваете ли Вы множества нечисловой природы в контексте понятия «алгебраическая структура» (множество векторов с операцией сложения, множество многочленов степени не выше п с операцией сложения, множество параллельных переносов с операцией композиции, множество классов чисел с операциями сложения и умножения и т.д.)?

12.Считаете ли Вы полезным проведение повторения с ярко выраженным характером теоретического обобщения?

13.Какой литературой Вы пользуетесь при повторении учебного материала по теме «Числовые множества»?

В результате опроса учителей выяснилось, что

1. Повторение темы «Числовые множества» происходит в основном ретроспективно.

2. Признаки делимости рассматриваются всегда только для ситуации делимости нацело.

3. Метод решения задач на делимость с выполнением операций над классами чисел применяют только лишь отдельные учителя (4%), излагая при этом фрагменты теории сравнений.

4. Свойства операций в подавляющем большинстве случаев связываются с природой элементов, участвующих в операции

На уроках не акцентируется внимание на том, что имеется некая общность при рассмотрении переместительного закона умножения чисел и, например, пе-реместительного закона сложения многочленов

5. Термины «группа», «кольцо», «поле» не употребляются, так как эти понятия в учебниках отсутствуют.

6. В учебной литературе нет систематизированного изложения учебного материала по понятию «число» (в контексте одного из ведущих понятий математики «алгебраическая структура»), которое носило бы характер обобщения теоретических знаний и практических умений.