Что означает термин «соответственно сонаправлены»?
Выражение «соответственно сонаправлены» означает, что два или несколько объектов, элементов или процессов взаимодействуют или движутся в одном направлении, дополняя друг друга в своей функции или цели.
Когда объекты, элементы или процессы являются соответственно сонаправлеными, они обладают сходством в своих свойствах, действиях или последовательностях. Их взаимосвязь подразумевает, что они функционируют совместно или исполняются последовательно для достижения общей цели.
Например, в технической сфере соответственно сонаправлеными могут быть два зубчатых колеса, которые входят в состав механизма. Когда одно колесо поворачивается в определенном направлении, другое колесо будет двигаться соответствующим образом, чтобы обеспечить передачу движения.
В бизнесе соответственно сонаправлеными могут быть различные этапы процесса производства товара. Каждый этап выполняется последовательно и дополняет предыдущий, чтобы достичь готового продукта.
Знание о том, какие элементы являются соответственно сонаправлеными, может быть полезным для понимания взаимодействия и взаимозависимости различных объектов, элементов или процессов в разных областях знаний или деятельности.
2)Теорема
Если прямая, не лежащая в данной
плоскости, параллельна какой-нибудь
прямой, лежащей в этой плоскости, то она
параллельна данной плоскости.
Доказательство
Рассмотрим плоскость άи две параллельные
прямые а и b,
расположенные так, что
прямая b
лежит в п
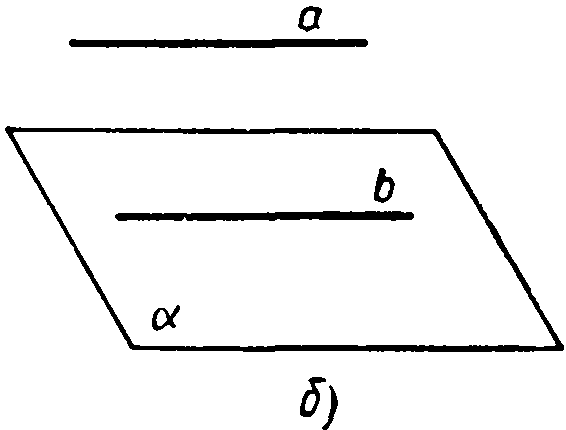
Теорема доказана.
Докажем еще два утверждения, которые
часто используются при решении задач.
1 . Если
плоскость проходит через данную прямую,
параллельную другой плоскости, и
пересекает эту плоскость, то линия
пересечения плоскостей параллельна
данной прямой.
П
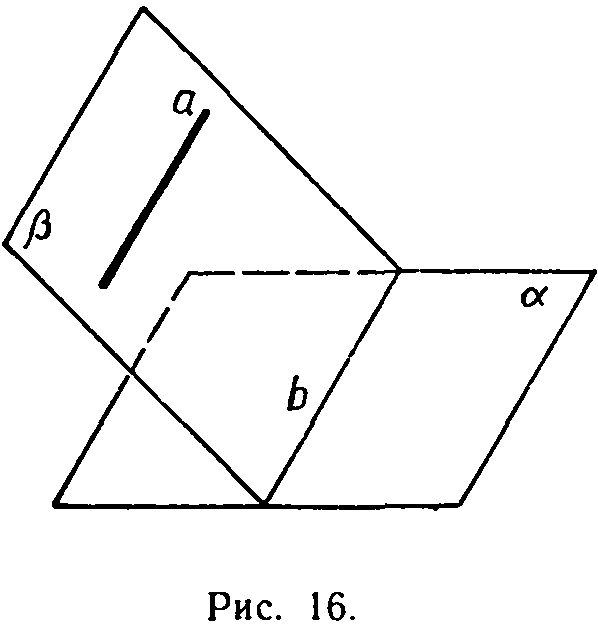
2°. Если одна
из двух параллельных прямых параллельна
данной плоскости, то другая прямая либо
также параллельна данной плоскости,
либо лежит в этой плоскости.
Важность соответственной сонаправленности в коммуникации
Важность соответственной сонаправленности заключается в том, что она способствует эффективному обмену информацией и позволяет достичь взаимопонимания между двумя сторонами коммуникации. Когда говорящий выражает свои мысли и идеи четко и ясно, а слушающий правильно и полно понимает его сообщение, возникает взаимное доверие и уважение
Примером соответственной сонаправленности может служить профессиональное общение в рабочей группе. Когда каждый участник группы владеет необходимой информацией, активно выражает свое мнение и точку зрения, а также умеет слушать и учитывать мнение других коллег, коммуникация становится эффективной и позволяет добиваться общей цели или решать различные задачи.
Соответственная сонаправленность также играет важную роль в межличностных отношениях. Когда люди активно слушают друг друга, демонстрируют эмпатию и уважение к идеям и мнениям другого человека, они создают теплую и поддерживающую атмосферу в общении.
В заключение, соответственная сонаправленность является фундаментальным элементом успешной коммуникации. Благодаря ей удается достичь взаимопонимания, сохранить хорошие отношения и добиться общих целей в рабочей группе или в межличностном общении.
Примеры сонаправленных векторов
Вот несколько примеров сонаправленных векторов:
1. Прямая ветвь дерева:
Если мы рассмотрим прямую ветвь дерева, то все ее подветви также будут иметь сонаправленные векторы, так как они имеют одно и то же направление и противоположное направление по отношению к стволу дерева.
2. Движение по прямой:
Если мы движемся по прямой линии в одном направлении, то скорость и ускорение будут иметь сонаправленные векторы. Например, если мы движемся вперед, то и скорость, и ускорение будут сонаправленными векторами в направлении движения.
3. Стрелки на одном направлении:
Если мы рассмотрим несколько стрелок, направленных на одно и то же направление, то все эти стрелки будут иметь сонаправленные векторы. Например, если все стрелки указывают вправо, то их векторы будут сонаправленными в направлении движения.
4. Силы, действующие на одно тело:
Если несколько сил действуют на одно тело, и эти силы имеют одно и то же направление или противоположное направление, то они будут иметь сонаправленные векторы. Например, если две силы действуют в одном направлении на тело, то векторы этих сил будут сонаправленными.
Это лишь некоторые примеры сонаправленных векторов. В реальном мире мы часто сталкиваемся с ситуациями, когда векторы имеют одинаковое направление или противоположное по направлению и равные или противоположные по модулю.
Действия с векторами. Коллинеарность векторов
В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.
Правило сложения векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора и :
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор от конца вектора :
Суммой векторов и является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов представляет собой вектор результирующего перемещения с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.
Кстати, если вектор отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.
Умножение вектора на число
Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».
Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.
Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация: (векторы сонаправлены) или (векторы направлены противоположно).
Произведением ненулевого вектора на число является такой вектор , длина которого равна , причём векторы и сонаправлены при и противоположно направлены при .
Правило умножения вектора на число легче понять с помощью рисунка:
Разбираемся более детально:
1) Направление. Если множитель отрицательный, то вектор меняет направление на противоположное.
2) Длина. Если множитель заключен в пределах или , то длина вектора уменьшается. Так, длина вектора в два раза меньше длины вектора . Если множитель по модулю больше единицы, то длина вектора увеличивается в раз.
3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны
Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.
4) Векторы сонаправлены. Векторы и также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.
Какие векторы являются равными?
Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».
С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.
Основные принципы соответственной сонаправленности
Основные принципы соответственной сонаправленности включают следующие:
| Принцип | Описание | Пример |
| Группировка связанных элементов | Элементы, имеющие сходное назначение или связанные функциональные возможности, должны быть сгруппированы вместе. |
<div class="header"> <h1>Заголовок</h1> <p>Подзаголовок</p> </div> |
| Организация данных в таблицы | Для представления табличных данных следует использовать теги , и . |
<table> <tr> <th>Имя</th> <th>Возраст</th> </tr> <tr> <td>Иван</td> <td>25</td> </tr> </table> |
| Использование списков для перечисления | Для перечисления элементов следует использовать теги , и . |
<ul> <li>Пункт 1</li> <li>Пункт 2</li> </ul> |
| Применение семантических тегов | Для выделения различных частей документа следует использовать семантические теги, такие как , , и другие. |
<header> <h1>Заголовок</h1> <nav> <a href="/">Главная</a> <a href="/about">О нас</a> </nav> </header> |
Соблюдение принципов соответственной сонаправленности упрощает понимание и изменение кода, а также улучшает доступность и оптимизацию веб-страницы.
Как вычислить косинус угла между векторами для определения их сонаправленности
Для определения того, являются ли два вектора сонаправленными, можно использовать косинус угла между ними. Косинус угла между двумя векторами равен скалярному произведению векторов, деленному на произведение их длин.
Таким образом, если результат вычисления косинуса угла между двумя векторами равен единице, то они являются сонаправленными. Если результат равен -1, то векторы противонаправлены, а если результат равен 0, то они перпендикулярны.
Для вычисления косинуса угла между двумя векторами необходимо вычислить скалярное произведение их координат и разделить его на произведение модулей (длин) векторов. Формула для вычисления косинуса угла между векторами выглядит следующим образом:
| cos(α) = | v1 ⋅ v2 | ÷ | |v1| × |v2| |
Здесь v1 и v2 — это координаты двух векторов, а ⋅ — это операция скалярного произведения. Модули векторов можно вычислить используя формулу:
| |v| = | √(vx2 + vy2 + vz2) |
Здесь vx, vy и vz — это координаты вектора v, которые могут быть равны нулю, если вектор находится на плоскости.
Найдя косинус угла между векторами, можно легко определить их сонаправленность и направление
Этот метод использован в различных областях, где важно понимать, как движутся или взаимодействуют различные объекты, имеющие определенное направление
Что такое векторы сонаправлены
Векторы сонаправлены — это понятие из линейной алгебры, которое описывает взаимное расположение двух или более векторов на одной прямой. Когда векторы сонаправлены, это означает, что они направлены в одну и ту же сторону и могут быть представлены как коллинеарные векторы.
Векторы сонаправлены имеют одинаковое направление, но могут отличаться по длине и ориентации. Направление вектора может быть положительным или отрицательным, в зависимости от того, в какой стороне он направлен относительно оси.
Векторы сонаправлены широко используются в физике, где они помогают описать движение объектов в пространстве. Например, при описании движения автомобиля по прямой дороге, вектор скорости и вектор ускорения будут сонаправлены, так как они указывают в том же направлении движения.
Другой пример векторов сонаправлены — это силы, действующие на объект. Если на объект действуют несколько сил, и их векторы сонаправлены, то можно сложить эти векторы для получения общей силы, действующей на объект.
Для определения того, что векторы сонаправлены, достаточно проверить, совпадают ли их направления. Если векторы направлены в одну и ту же сторону или противоположны друг другу, то они сонаправлены и могут быть представлены как коллинеарные векторы.
Пример:
- Вектор A = (3, 4) и вектор B = (6,
 являются сонаправленными, так как они имеют одинаковое направление и могут быть умножены на одно и то же число.
являются сонаправленными, так как они имеют одинаковое направление и могут быть умножены на одно и то же число. - Вектор C = (-2, 1) и вектор D = (-4, -2) также являются сонаправленными, так как они имеют противоположное направление.
- Вектор E = (1, 3) и вектор F = (-1, -3) не являются сонаправленными, так как они имеют противоположное направление.
Векторы сонаправлены являются важным понятием в линейной алгебре и находят применение в различных областях науки и техники.
Векторы сонаправлены в математике
Векторы в математике представляют собой объекты, которые имеют как величину, так и направление. Они широко используются в различных областях, включая физику, геометрию, информатику и технику. Когда речь идет о векторах, одно из важнейших понятий, которое нужно понимать, — это сонаправленность.
Векторы сонаправлены, если они имеют одно и то же направление или показывают в одну сторону. Иными словами, если два вектора смотрят в одном направлении или находятся на одной прямой, они сонаправлены. Обратное утверждение также верно: если два вектора сонаправлены, это означает, что они смотрят в одном направлении или находятся на одной прямой.
Сонаправленность векторов можно описать с помощью следующих условий:
- Если два вектора направлены в одну сторону, они сонаправлены.
- Если два вектора параллельны, они сонаправлены.
- Если два вектора имеют одинаковые направления, они сонаправлены.
Сонаправленные векторы могут иметь различные величины, но при этом они все равно будут указывать в одном направлении. Это означает, что если мы добавим ко второму вектору или умножим его на какое-либо число, он все равно будет сонаправлен первому вектору.
Пример:
| Вектор 1 | Вектор 2 | Вектор 3 |
|---|---|---|
| 5i | 10i | -3i |
| 2j | 4j | -1j |
Векторы 1 и 2 сонаправлены, так как они имеют одинаковые направления и указывают в одном направлении. Вектор 3 сонаправлен с векторами 1 и 2, хотя и имеет отрицательное направление.
Векторы сонаправлены играют важную роль во многих приложениях, таких как физические законы, расчеты сил и перемещений, определение прямых и плоскостей в геометрии, а также в алгоритмах компьютерной графики и машинном обучении.
Что значит быть соответственно сонаправленным?
Быть соответственно сонаправленным подразумевает, что два или более объекта имеют единое направление действий или целей. Например, в бизнесе, когда компания и ее сотрудники работают вместе и стремятся достичь общей цели, они считаются соответственно сонаправленными. Это обеспечивает согласованность и синхронизацию в работе, что может привести к улучшению результатов и эффективности.
Примером соответственного сонаправления может служить работа команды разработчиков программного обеспечения над одним проектом. Каждый член команды имеет свои специализации и задачи, однако они все движутся в одном направлении, соблюдая соглашения и сотрудничая для достижения общей цели — успешного завершения проекта.
Еще одним примером соответственного сонаправления является движение двух автомобилей, двигающихся по одной дороге в одном направлении с одинаковой скоростью и соблюдая правила дорожного движения. В этом случае, два автомобиля считаются соответственно сонаправленными, так как они движутся в одном направлении и совершают одинаковые действия — перемещаются по дороге.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.



Конспект урока «Углы с сонаправленными сторонами»
· введем понятие сонаправленных лучей;
· дадим определение сонаправленных лучей;
· докажем теорему о равенстве углов с сонаправленными сторонами.
На этом уроке нам понадобится одна из аксиом планиметрии, которая звучит следующим образом: «любая прямая разбивает плоскость на две полуплоскости».
Итак, пусть у нас есть некоторая прямая а, которая лежит в плоскости α. Согласно аксиоме, эта прямая разделяет плоскость α на две части. Каждую из которой, называют полуплоскостью.
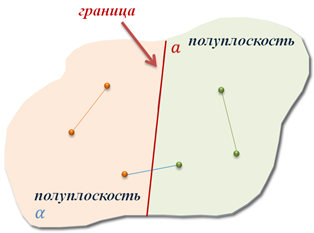
Понятно, что наша прямая а разделила плоскость α на две полуплоскости. Одна из которых лежит слева от прямой а, вторая – справа. В свою очередь, прямую а называют границей каждой из этих полуплоскостей.
Обратите внимание, любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а. А вот любые две точки разных полуплоскостей лежат по разные стороны от этой прямой
Определение. Два луча ОА и О1А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО1.
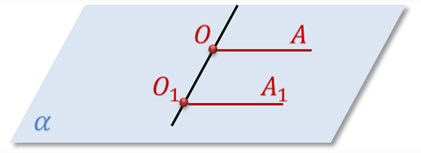
Напомню, что два луча называются параллельными, если они лежат на параллельных прямых.
Лучи ОА и O1A1, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Докажем теорему об углах с сонаправленными сторонами.
Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.
Доказательство. Рассмотрим случай, когда углы О и О1 с соответственно сонаправленными сторонами лежат в разных плоскостях.
Пусть нам даны параллельные лучи ОА и О1А1 и параллельные лучи ОB и
О1B1. Т.е. мы имеем два угла АОB и А1О1B1, стороны которых лежат на сонаправленных лучах. Докажем, что угол АОB равен углу А1О1B1.
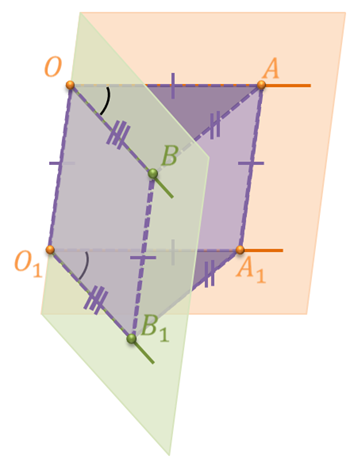
Отметим на сторонах лучей ОА и O1A1 точки А и A1 так, чтобы отрезки ОА и O1A1 были равны. На сторонах лучей ОB и O1B1 отметим точки B и B1 так, чтобы отрезки ОB и O1B1 были равны.
Рассмотрим четырехугольник ОАA1O1. Так как лучи ОА и O1A1 параллельны по условию (сонаправленны ) и равны по построению, то четырехугольник ОАА1О1 является параллелограммом по признаку параллелограмма. Следовательно, АА1 параллельно ОО1 и АА1 равно ОО1.
Рассмотрим четырехугольник ОBB1O1. Его стороны ОB и O1B1 параллельны, т.к. лежат на сонаправленных лучах по условию и равны по построению. Значит, по признаку параллелограмма четырехугольник OBB1O1 является параллелограммом. Тогда, стороны BB1 и OO1 параллельны и равны.
Обратите внимание, мы получили, что прямая AA1 параллельна прямой OO1 и прямая BB1 параллельна прямой OO1. Тогда по признаку параллельности прямых в пространстве, прямые AA1 и BB1 параллельны
Рассмотрим четырехугольник BAA1B1. В этом четырехугольнике стороны AA1 и BB1 параллельны и равны. А значит, BAA1B1 – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A1B1 тоже параллельны и равны.
Теперь рассмотрим треугольники АОB и A1O1B1. Стороны ОА и O1A1 равны по построению. Стороны ОB и O1B1 также равны по построению. Выше мы доказали, что стороны АB и A1B1 равны. Значит, треугольники АОB и A1O1B1 равны по трем сторонам. Напомню, что в равных треугольниках против соответственно равных сторон лежат равные углы. Значит, углы АОB и A1O1B1 равны. Теорема доказана.
Задание. Рассмотрите рисунок и
а) укажите лучи, которые являются сонаправленными;
б) укажите лучи, которые не являются сонаправленными.
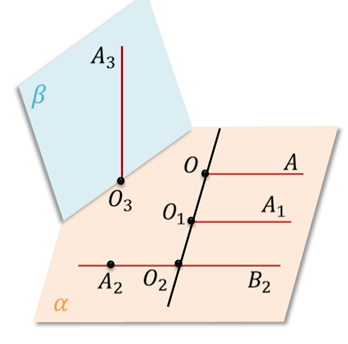

Подведем итоги урока. На этом уроке мы ввели понятие сонаправленных лучей. Узнали, что два луча ОА и О один А один в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей О О один. Лучи ОА и О один А один, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой. А также доказали теорему о равенстве углов с сонаправленными сторонами.
Источник
Примеры вычисления косинуса угла между двумя векторами
Вычисление косинуса угла между двумя векторами является одним из ключевых понятий линейной алгебры. Для его определения необходимо знание скалярного произведения векторов.
Пусть имеются два вектора A и B в трехмерном пространстве. Для вычисления косинуса угла между ними достаточно разделить скалярное произведение на произведение модулей векторов:
cos α = (A · B) / (|A| * |B|)
Для наглядности можно привести пример с координатами: если A(2,3,4) и B(5,6,7), то:
cos α = ((2*5) + (3*6) + (4+7)) / (√(2²+3²+4²) * √(5²+6²+7²)) = 0.994
Таким образом, косинус угла между этими векторами составляет 0.994, что означает, что они сонаправлены.
Если же косинус угла равен 0, то векторы ортогональны (то есть перпендикулярны друг другу), а если косинус угла меньше 0, то они направлены в противоположных направлениях.
Использование онлайн-калькулятора
Решение простых заданий из школьного курса обычно не вызывает сложностей. Но на практике приходится сталкиваться со сложными выражениями. Для их вычисления нужно проявить усидчивость и при этом быть предельно внимательным. Кроме этого, расчёт занимает довольно много времени, а любая, казалось бы, незначительная оплошность, приведёт к неправильному решению.
Поэтому условие коллинеарности векторов удобно проверять на так называемых онлайн-калькуляторах. Это обычно мощные сервисы, основная деятельность которых заключается в предоставлении услуг по автоматизации вычислений. Среди них попадаются и сайты, умеющие вычислять и вектора.
Для того чтобы выполнить на них математические операции, необходимо иметь доступ к интернету и установленный веб-обозреватель. Всё, что требуется от пользователя, это просто зайти на сайт и выбрать раздел, связанный с операциями над векторами. Затем в предложенную форму вести условие задания и запустить расчёт нажатием одной кнопки.
Из множества онлайн-расчётчиков, доступных в секторе рунета, можно выделить следующие:

- SolverBook — это простой на вид сайт, содержащий на своей странице приложение, позволяющее выполнять любые действия над отрезками, а также определять их вид. Кроме непосредственного предоставления ответа, сервис выдаёт пошаговое решение. При этом каждый этап будет детально расписан.
- O nlineMSchool — сайт помогает найти коллинеарные отрезки для любой сложности примеров. На страницах сервиса находится вся необходимая теория и примеры решения заданий. Поэтому даже слабо подготовленный пользователь сможет разобраться во всех нюансах решения нужных ему задач.
- Kontrolnaya-rabota — отличительной его чертой является возможность отправления подробного решения на указанную электронную почту. Сайт умеет работать как с парой векторов, так и попарной системой.
Все указанные сервисы предоставляют доступ к услугам бесплатно и без регистрации. Воспользовавшись онлайн-калькуляторами, даже слабо подготовленный пользователь научится самостоятельно определять коллинеарность. Такие расчётчики будут полезны и учащимся, и инженерам.
Задачи на умножение сонаправленных векторов на число для 9 класса
Вот несколько задач, в которых нужно умножать сонаправленные векторы на число:
- Вектор AB имеет длину 5 см и направлен вправо. Найдите вектор BC, если он получается путем умножения вектора AB на число 3.
- Вектор PQ имеет длину 10 м и направлен вверх. Найдите вектор QR, если он получается путем умножения вектора PQ на число 2.
- Вектор XY имеет длину 15 км и направлен вниз. Найдите вектор YZ, если он получается путем умножения вектора XY на число 4.
Для решения этих задач нужно умножить длину исходного вектора на заданное число, не меняя его направления. В результате получим новый вектор, который и будет искомым.
Используя умножение сонаправленных векторов на число, можно решать различные задачи, связанные с изменением длины вектора. Это огромное применение находит в реальной жизни, например, в физике, строительстве и навигации.
Изображение
Векторные элементы необходимо грамотно изображать, а не только записывать. Скаляр будет выражаться конкретной точкой на числовой прямой.
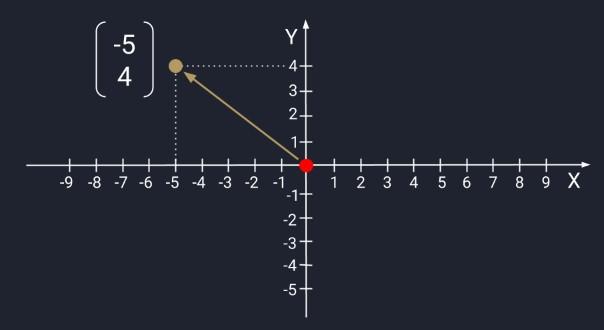
Компонент, который называется вектором и состоит из двух чисел – это две точки на плоскостях X и Y. Числа будут задавать координаты рассматриваемого элемента в пространстве. Они представляют собой некоторую инструкцию перемещения от хвоста к стрелке. Первое число – это расстояние, которое отмечается по оси X, второе – по Y. Положительные числа на X указывают движение вправо, отрицательные – влево. В случае с Y положительные параметры – это движение вверх, отрицательные – вниз.
Если координаты три, то изображение осуществляется на плоскостях X, Y, Z. Ось Z будет проводиться перпендикулярно X и Y. Такая форма записи называется трехмерной. Вектор здесь представлен триплетом чисел:
- первые два указывают на движение по X и Y;
- третье – куда направляться по оси Z.
Каждый триплет формирует уникальный «направленный отрезок» в пространстве. Каждый компонент, который называется вектором, имеет всего один триплет.
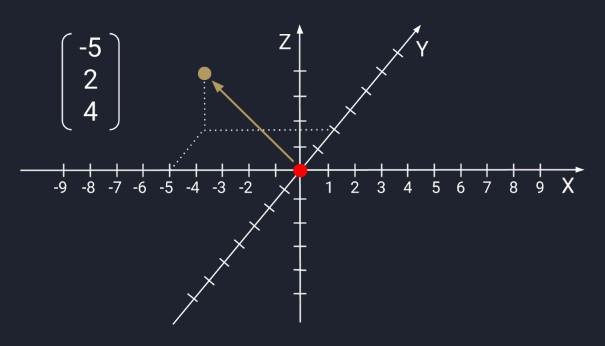
Выше – наглядный пример изображения рассматриваемых математических составляющих в трехмерном пространстве. Обычно в программировании и обучении используются двухмерные пространства и записи.
Определение сонаправленных векторов
Для определения сонаправленных векторов необходимо учитывать следующее:
- Векторы должны быть ненулевыми, то есть они должны иметь ненулевую длину.
- Длины векторов могут отличаться, но это не влияет на их сонаправленность. Главное, чтобы они указывали в одном направлении.
- Векторы могут быть параллельными или антипараллельными. Параллельные векторы сонаправлены, тогда как антипараллельные имеют противоположное направление, но также сонаправлены.
Сонаправленные векторы можно представить графически, например, стрелками, указывающими в одном направлении. Векторы могут иметь как положительное, так и отрицательное направление в зависимости от выбранной системы координат.
Примером сонаправленных векторов может служить движение автомобилей по одной и той же дороге в одном направлении. Векторы скорости этих автомобилей будут сонаправленными, так как они указывают в одном направлении — вперед.
Понятие скрещивающихся прямых
В пространстве можно построить две прямые так, что они не будут пересекаться, но и параллельными они также являться не будут. Для этого достаточно, чтобы прямые НЕ находились в одной плоскости. В этом случае их именуют скрещивающимися прямыми.

Здесь ребра ВС и АЕ как раз лежат на двух скрещивающихся прямых. Поэтому их можно так и называют – скрещивающиеся отрезки. По аналогии можно ввести понятие и скрещивающихся лучей.
Существует теорема, представляющая собой признак скрещивающихся прямых.

Действительно, пусть есть две прямые, НК и РМ. Обозначим как α плос-ть, проходящую через НК и точку М. Если РМ пересекает α, то это означает, что М – единственная общая точка у α и РМ. Получается, что Н, К, М и Р – это точки в различных плос-тях, и через них нельзя провести одну плос-ть. Значит, и прямые НК и РМ – скрещивающиеся.

Таким образом, в стереометрии возможно всего три случая взаимного расположения двух прямых в пространстве:
1) прямые пересекаются, и тогда они обязательно находятся в одной плос-ти;
2) прямые располагаются в одной плос-ти, но не пересекаются – случай параллельных прямых;
3) прямые находятся в разных плос-тях – случай скрещивающихся прямых.

Докажем одну теорему:

Для доказательства возьмем произвольные скрещивающиеся прямые m и n. Отметим на n точку К и проведем через К прямую р, параллельную m:

Через пересекающиеся прямые nи p можно провести единственную плос-тьα. По признаку параллельности прямой и плос-ти можно заключить, что m||α.
Покажем, что кроме α нет других плос-тей, проходящих через n и параллельных m. Действительно, если бы такая плос-ть β существовала, то р имела бы с ней общую точку К, но полностью в β она бы не могла находиться, иначе α и β совпадали бы. Значит, р пересекала бы β. Но тогда ее обязательно пересекала бы и m по одну из свойств параллельных прямых. В этом случае m и β не были бы параллельными.
Примеры в геометрии и приложениях
Сонаправленные вектора находят широкое применение в геометрии и других приложениях. Вот несколько примеров:
1. Векторные операции:
Сонаправленные вектора используются во многих векторных операциях, таких как сложение, вычитание и умножение векторов на скаляр. Например, при сложении двух сонаправленных векторов их значением будет вектор с той же направленностью и суммой их длин.
2. Соотношение между векторами и их компонентами:
Сонаправленные вектора позволяют установить соотношение между векторами и их компонентами. Например, если имеется вектор сонаправленный оси координат, его компоненты относятся к основным направлениям соответствующих осей.
3. Вычисление проекций:
Сонаправленные вектора широко используются для вычисления проекций векторов на плоскости или на оси. Например, при проецировании вектора на плоскость, проекции будут иметь одинаковое направление.
4. Расчет сил и скоростей:
В физике сонаправленные вектора применяются для расчета сил и скоростей. Например, сила, направленная вдоль оси, может быть представлена как сонаправленный вектор, а его величина будет определять величину силы.
5. Анализ направления и углов:
Сонаправленные вектора используются для анализа направления и углов между ними. Например, можно определить угол между двумя сонаправленными векторами, используя угловую функцию их компонент.
Все эти примеры показывают, что понимание и работы с сонаправленными векторами является важной частью геометрии и имеет широкий спектр приложений
Как работает сонаправленный вектор?
Сонаправленный вектор — это вектор, который имеет направление, совпадающее с другим вектором, но может иметь другую длину. Это означает, что при перемножении двух векторов, если они сонаправлены, мы получим новый вектор, который будет иметь направление совпадающее с направлением этих двух векторов.
Сонаправленный вектор может использоваться для удобства при задании векторов в пространстве. Например, если мы знаем направление вектора, но не знаем его точных координат, мы можем задать этот вектор как сонаправленный вектор с базовым вектором, имеющим известные координаты. Это упрощает вычисления и позволяет быстрее решать задачи в линейной алгебре и геометрии.
Сонаправленный вектор может также использоваться в физике для определения точного направления силы и ее векторной суммы. Например, если у нас есть две или более сил, направленные в одном направлении, мы можем использовать их сонаправленный вектор, чтобы определить общее направление силы и их векторную сумму. Это помогает упростить расчеты и обеспечить более точные результаты в физических экспериментах.
Как достичь соответственной сонаправленности
Чтобы достичь соответственной сонаправленности в отношениях, необходимо уделить внимание следующим аспектам:
1
Общие ценности: важно, чтобы у вас и вашего партнера были схожие ценности и убеждения. Обсудите, что вам действительно важно и на чем вы фокусируетесь в жизни.
2
Общие цели и планы: определите, какие цели вы хотите достичь вместе и разработайте план действий, чтобы их достичь. Важно, чтобы вы оба стремились к одним и тем же результатам.
3. Взаимная поддержка: поддерживайте друг друга в достижении поставленных целей. Будьте готовы помогать и поддерживать своего партнера в трудные моменты.
4. Взаимопонимание и компромисс: находите общий язык, разбирайтесь во взаимных потребностях и находите компромиссы, чтобы удовлетворить обе стороны.
5. Открытость и честность: будьте открытыми и честными друг с другом. Доверие и искренность являются ключевыми элементами соответственной сонаправленности.
6. Общение: уделите время для открытого общения друг с другом. Слушайте и понимайте друг друга, выражайте свои мысли, чувства и потребности.
Следуя этим принципам, вы можете достичь соответственной сонаправленности в отношениях и создать гармоничную и счастливую совместную жизнь.
3.1 Понятие atomic вектора в R
Если у вас не было линейной алгебры (или у вас с ней было все плохо), то просто запомните, что вектор (atomic vector или просто atomic) – это набор (столбик) чисел в определенном порядке.
Если вы привыкли из школьного курса физики считать вектора стрелочками, то не спешите возмущаться и паниковать. Представьте стрелочки как точки из нуля координат {0,0} до какой-то точки на координатной плоскости, например, {2,3}:
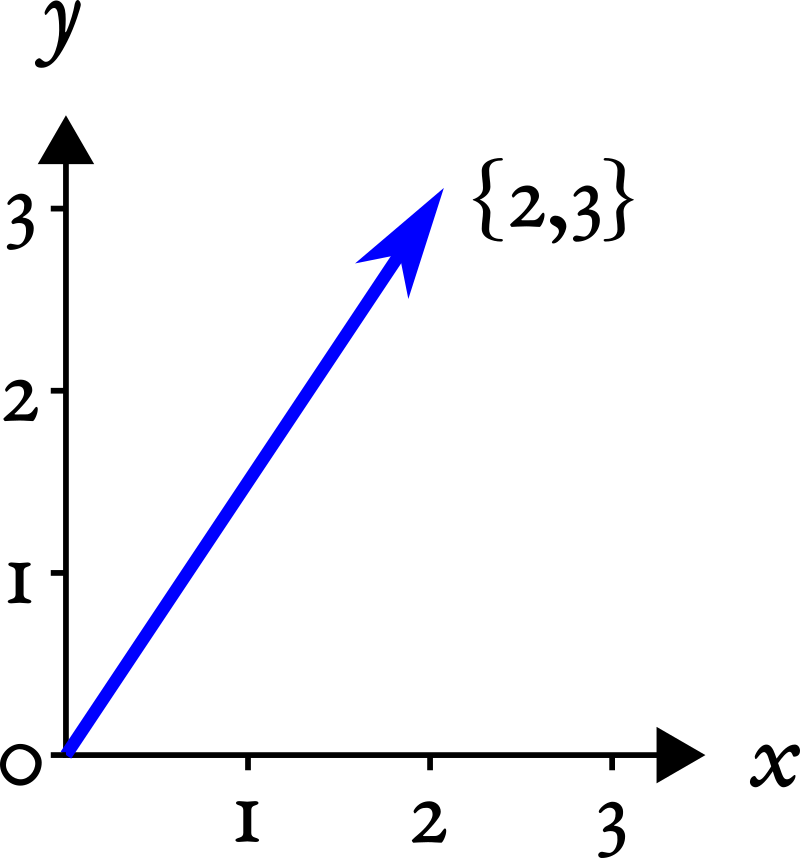
Вот последние два числа и будем считать вектором. Попытайтесь теперь мысленно стереть координатную плоскость и выбросить стрелочки из головы, оставив только последовательность чисел {2,3}:

На самом деле, мы уже работали с векторами в R, но, возможно, вы об этом даже не догадывались. Дело в том, что в R нет как таковых скалярных (т.е. одиночных) значений, есть вектора длиной 1. Такие дела!
Чтобы создать вектор из нескольких значений, нужно воспользоваться функцией :
Осторожно: ошибка с кириллической “с”
Одна из самых мерзких и раздражающих причин ошибок в коде – это использование из кириллицы вместо из латиницы. Видите разницу? И я не вижу. А R видит. И об этом сообщает:
Для создания числовых векторов есть удобный оператор .
Этот оператор создает вектор от первого числа до второго с шагом 1. Вы не представляете, как часто эта штука нам пригодится… Если же нужно сделать вектор с другим шагом, то есть функция :
Кроме того, можно задавать не шаг, а длину вектора. Тогда функция сама посчитает шаг:
Другая функция – – позволяет создавать вектора с повторяющимися значениями. Первый аргумент – значение, которое нужно повторять, а второй аргумент – сколько раз повторять.
И первый, и второй аргумент могут быть векторами! Если второй агрумент – вектор такой же длины, то каждое значение первого вектора будет повторено соответствующее количество раз из второго вектора.
Если нужно повторить каждое значение в векторе одно и то же количество раз, то можно воспользоваться дополнительным параметром :
Еще можно объединять вектора (что мы, по сути, и делали, просто с векторами длиной 1):
Очень многие функции в R работают именно с векторами. Например, функции (считает сумму значений вектора) и (считает среднее арифметическое всех значений в векторе):


























