Угол ⭐ между прямой и плоскостью в пространстве: определение, как найти, свойства, формула и примеры

Плоскость и ее основные свойства

Рассмотрим свойства плоскости, которые обычно принимаются без доказательств, поскольку это аксиомы:

Когда каждые 2 точки, которые лежат на одной прямой, принадлежат к единой плоскости, то все точки, находящиеся на этой прямой, также будут принадлежать к данной плоскости.
Если 2 плоскости соприкасаются в одной точке, значит они будут пересекаться на прямой линии, проходящей через эту точку.
Для любых 3 точек, не принадлежащих одной прямой, можно нарисовать плоскость, причем только одну.

Последствия этих аксиом следующие:

Можно нарисовать плоскость, имеющую прямую линию и точку за ней. Действительно утверждение, что точка вне прямой линии вместе с любыми двумя точками, лежащими на прямой, буду образовывать три точки, через которые может пройти новая плоскость.
Через две пересекающиеся линии можно провести единственную плоскость. Если взять точку пересечения и еще одну точку на прямой, то получим 3 точки, через которые можно будет провести единственную плоскость.
Только одну плоскость можно нарисовать двумя параллельными линиями. Доказано, что две параллельные прямые по определению лежат в одной плоскости. Эта плоскость уникальна, потому что не более одной плоскости можно провести через одну параллельную плоскость и одну точку в другую.
Вращение плоскости по прямой. Поэтому можно провести бесчисленное количество плоскостей через любую линию в пространстве.

Доказательство:

Действительно, пусть это будет прямая линия.
Возьмите отдельно точку А.
Через А и данную прямую а проходит плоскость М.
Возьмем точку B, лежащую вне данной плоскости М.
Через данную точку В и прямую линию также будет проходить плоскость N, которая может не совпадать с М. Это связано с тем, что она имеет точку B и она не принадлежит к М плоскости.
Мы можем взять другую точку С в пространстве за плоскости М и N.
Через точку С и прямой пройдет новая плоскость, например Р. Она не совпадет с М, ни с N, потому что содержит точку С, которая не принадлежит плоскости М и плоскости N.

Продолжая занимать все новые и новые точки в пространстве, мы получаем все больше и больше плоскостей. Они все будут пересекать исходную линию.

Их может быть бесчисленное число. Все полученные плоскости можно рассматривать как различные повороты одной исходной плоскости, которая может будет вращаться вокруг прямой А.

Таким образом, мы можем найти еще одно качество плоскости, которая может вращаться вокруг прямой, принадлежащей к ней.

Прямые в пространстве

Рассмотрим признаки параллельности прямых относительно заданной плоскости в пространстве:

Если 2 прямые линии в исходном пространстве параллельны, то они будут лежать в одной плоскости, поэтому пересекаться не могут.
Когда 2 линии пересекаются в пространстве, значит они не принадлежат к одной плоскости.
Когда прямая линия лежит на заданной плоскости, а другая пересекает данную плоскость в определенной точке, значит они будут пересекаться.
Прямые параллельны, если они не имеют общих точек соприкосновения.
Когда прямая не лежит на исходной плоскости, но параллельна относительно прямой, лежащей на этой плоскости, то они полностью параллельны.

Теорема о трех перпендикулярах на плоскости

Чтобы прямая линия, которая лежит в данной плоскости, была к ней перпендикулярна, вполне достаточно, чтобы она была перпендикулярна к проекции данной плоскости.

Любой угол между линией и плоскостью — это угол между линией и ее выступом на плоскости. Когда прямая b наклонна к исходной плоскости, то прямая а будет проекцией этой наклонной, а угол α будет находиться между наклонной и заданной плоскостью.

Любая прямая, которая получена при пересечении 2 плоскостей, будет называться ребром двугранного угла. Полуплоскости с одним общим ребром называют треугольными угловыми гранями.

Если граница полуплоскости совпадает с краем двугранного угла и делит двугранный угол на два равных, то ее называют биссектрисой.

Угол с двойными стенками можно измерять соответствующим линейным углом. Линейный угол для любого двугранного угла является углом между перпендикулярами, проведенными к каждой грани, и ее краем.

Метод с использованием векторов: значение

Основой для метода с использованием векторов является понятие вектора нормали плоскости. Вектор нормали определяется как вектор, перпендикулярный плоскости и указывающий в направлении от нее. Для того чтобы найти вектор нормали, необходимо знать координаты нормального вектора прямой, проходящей через плоскость.

Зная вектор нормали плоскости и координаты точки, принадлежащей прямой, можно найти уравнение плоскости, проходящей через прямую. Уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C — коэффициенты нормального вектора, а D — свободный член.

После того как уравнение плоскости найдено, можно перейти к решению конкретных задач. Например, для того чтобы найти угол между прямой и плоскостью, необходимо воспользоваться формулой cos(α) = |a·n| / (|a| · |n|), где a — направляющий вектор прямой, n — вектор нормали плоскости.

Также, если необходимо найти точку пересечения плоскости с прямой, можно воспользоваться системой уравнений, состоящей из уравнения плоскости и уравнения прямой. Решив эту систему, получим координаты искомой точки пересечения.

Решение задач

Аксиомы стереометрии часто применяются в доказательствах. И ещё в задачах с открытыми вопросами. Вот пример такой задачи:

Задача 1. Окружность и плоскость

Решение. Легко заметить, что ответ зависит от взаимного расположения точек $M$, $N$ и $O$.

Допустим, что все они лежат на одной прямой. Тогда $MN$ — диаметр, и вся окружность может как лежать в плоскости $\alpha $, так и не лежать в ней. Вот пример когда окружность не лежит в плоскости:

Пусть теперь точки $M$, $N$ и $O$ не лежат на одно прямой. По Аксиоме плоскости (Аксиома 4 в нашем списке) эти точки однозначно задают плоскость. Эта плоскость совпадает с плоскостью $\alpha $.

А поскольку окружность — плоская фигура, то остальные её точки также принадлежат плоскости $\alpha $:

Задача 2. Неравильный рисунок

Решение. Соединим точки $M$ и $K$ прямой $l$:

Мы видим, что точка $B\notin l$. Поэтому точки $M$, $B$, $K$ не лежат на одной прямой. И согласно Аксиоме плоскости (Аксиома 4 в нашем списке), эти точки однозначно задают плоскость.

С одной стороны, мы видим по рисунку, что это плоскость $\alpha $. С другой стороны, параллелограмм — плоская фигура, поэтому точки $M$, $B$, $K$ лежат ещё и в плоскости параллелограмма. А это значит, что плоскости $\alpha $ и $ABCD$ должны совпадать, чего на рисунке не происходит.

Есть и другой способ показать, что рисунок некорректен. По условию задачи, точки $M$, $B$, $K$ являются общими для плоскости $\alpha $ и плоскости $ABCD$. Согласно Аксиоме пересечения плоскостей (Аксиома 5 в нашем списке), все эти точки должны лежать на одной прямой.

Однако простое построение показывает, что точки $M$, $B$, $K$ не лежат на одной прямой, что противоречит аксиоме. Такое противоречие как раз и доказывает некорректность чертежа.

Далее мы будем лишь называть аксиомы — без нумерации.

Задача 3. Прямые на плоскости

Решение. Нарисуем прямые $a$, $b$, $c$ и обозначим их точки пересечения $M$, $N$, $K$:

Точки $M$, $N$, $K$ не лежат на одной прямой. По основной Аксиоме плоскости, эти три точки однозначно определяют некоторую плоскость $\alpha $.

Далее заметим, например, что точки $M\in \alpha $ и $N\in \alpha $ по построению. По основной Аксиоме прямой и плоскости вся прямая $MN=b$ лежит в этой плоскости, т.е. $b\subset \alpha $.

Аналогично доказывается, что прямые $a\subset \alpha $ и $b\subset \alpha $.

Задача 4. Пересечение плоскостей

Решение. Обозначим прямую, по которой пересекаются плоскости $\alpha $ и $\beta $, буквой $l$:

Дополнительное построение: прямая $AB$, которая пересекает прямую $l$ в точке $M$:

Точки $A\in \alpha $, $B\in \alpha $. По основной Аксиоме прямой и плоскости прямая $AB\subset \alpha $ — искомая линия сечения плоскости $\alpha $ и $ABC$.

Далее заметим, что точка $M\in l\subset \beta $. Дополнительное построение: прямая $CM$:

Точки $C\subset \beta $, $M\subset \beta $. И вновь по основной Аксиоме прямой и плоскости прямая $CM$ — искомая линия сечения плоскости $\beta $ и $ABC$.

Хочу отметить, что задачи на построение — это отдельный класс задач. Как в планиметрии, так и в стереометрии. Там много интересных моментов, им посвящены отдельные уроки. А то, что мы сделали сейчас — это совсем уж простые рассуждения, которые тем не менее опираются на всю мощь аксиом.

Задача 5. Стандартное доказательство

Решение. Это классическая задача на доказательство, которую в разных формулировках предлагают во всех учебниках по стереометрии.

Обозначим параллелограмм $ABCD$. Пусть $O$ — точка пересечения диагоналей.

Поскольку точка $O\notin AB$, точки $A$, $B$, $O$ не лежат на одной прямой. По основной Аксиоме плоскости эти три точки однозначно определяют плоскость. Обозначим эту плоскость $\alpha $.

Точки $A\in \alpha $, $O\in \alpha $. По основной Аксиоме прямой и плоскости, прямая $AO\subset \alpha $. Но точка $C\in AO\subset \alpha $. Следовательно, вершина параллелограмма $C\in \alpha $. Аналогично через точки $B$ и $O$ доказывается, что вершина $D\in \alpha $.

Замечание по поводу задач

Как видите, мы рассмотрели лишь самые простые задачи

Но даже на их примере видно, насколько важно чётко знать систему аксиом

Бесчисленное множество контрольных и экзаменов были завалены просто потому, что ученик не смог обосновать простые и наглядные рассуждения. Потому что, например, не знал: можно ли утверждать, что если две точки прямой лежат на плоскости, то и вся прямая лежит на этой плоскости.

В общем, учите аксиомы и практикуйтесь на простых примерах. А для более интересных задач нам потребуются некоторые следствия из этих аксиом. Чему и посвящён следующий урок.:)

Следствия из аксиом стереометрии
Теорема о трёх перпендикулярах
Комментарий к пробному ЕГЭ от 7 декабря
Метод Гаусса
Задачи про температуру и энергию звезд
Задача B4 про шерсть и свитер

Нормальное уравнение плоскости

Нормальным уравнением плоскости называется уравнение: (6.4)

где — углы между перпендикуляром, опущенным из начала координат на плоскость, и положительным направлением осей координат, а p- расстояние от плоскости до начала координат.

Нормальное уравнение отличается от общего уравнения тем, что в нем коэффициенты при x, у, z являются координатами единичного вектора перпендикулярного плоскости, а свободный член — отрицательный.

Общее уравнение (1) приводится к нормальному виду умножением его на нормирующий множитель при этом знак выбирается противоположным знаку свободного члена D (если D = 0, знак можно выбрать любой).

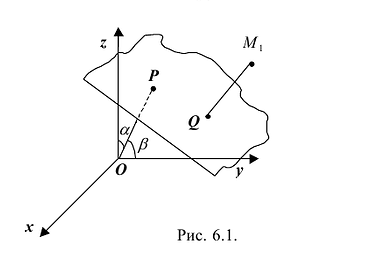
Отклонением точки , от плоскости называется ее расстояние d от плоскости, взятое со знаком плюс, если точка и начало координат О лежат по разные стороны от плоскости (Рис. 6.1), и со знаком минус — если и О лежат по одну сторону от плоскости.

Отклонение точки от плоскости определяется по формуле

Следовательно, чтобы найти расстояние от точки до плоскости, надо привести уравнение плоскости к нормальному виду и в его левую часть вместо х, у, z подставить координаты точки . Получим отклонение . А расстояние .

Уравнение прямой, проходящей через две точки.

Пусть в пространстве задана общая декартова система координат и две точки $M_{1}$ и $M_{2}$ с координатами $(x_{1}, y_{1}, z_{1})$ и $(x_{2}, y_{2}, z_{2})$. Чтобы написать уравнение прямой $M_{1}M_{2}$, примем $M_{1}$ за начальную точку, a $\overrightarrow{M_{1}M_{2}}$ за направляющий вектор. Этот вектор не нулевой, если точки не совпадают. По формуле мы получаем
$$
\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}.\label{ref1}
$$
Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять нулю соответствующий числитель.

В планиметрии задача решается также. Отличие только в том, что координаты точек теперь $(x_{1}, y_{1})$ и $(x_{2}, y_{2})$, и мы получаем по
$$
\begin{vmatrix}
x-x_{1}& y-y_{1}\\
x_{2}-x_{1}& y_{2}-y_{1}
\end{vmatrix}
= 0.\nonumber
$$

Расстояние от точки до плоскости.

Пусть дана плоскость с уравнением $(\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})=0$ и точка $M$ с радиус-вектором $R$. Рассмотрим вектор $\overrightarrow{M_{0}M}=\boldsymbol{R}-\boldsymbol{r}_{0}$, соединяющий начальную точку плоскости с $M$ (рис. 7.1). Расстояние от точки до плоскости равно модулю его скалярной проекции на вектор $\boldsymbol{n}$, то есть
$$
h=\frac{|(\boldsymbol{R}-\boldsymbol{r}_{0}, \boldsymbol{n})|}{|\boldsymbol{n}|}.\label{ref6}
$$

Если в декартовой прямоугольной системе координат точка $M$ имеет координаты $(X, Y, Z)$, то равенство \eqref{ref6} запишется согласно ранее доказанным утверждениям ( и ) так:
$$
h=\frac{|AX+BY+CZ+D|}{\sqrt{A^{2}+B^{2}+C^{2}}}.\label{ref7}
$$

Рис. 7.1. Расстояние от точки до плоскости.

Сечения

Как дракон с помощью сечений разрушал город?

…В далеком будущем, на одной из недавно открытых планет, люди построили новую цивилизацию. Они возвели новые дома для комфортной жизни разных необычных форм.

Он прилетал к домам, раскрывал свою пасть и стрелял страшным красным лучом. И каждая поверхность и каждый объем, которого касался этот луч, разрезался по прямой линии.

Прилетел дракон к пирамиде и разрезал ее. Ахнули люди: верхушка пирамиды съехала, осталась лишь прямоугольная плоскость.

Увидел дракон обычный дом — в форме параллелепипеда, — и снова луч разрезал здание. Осталась вместо крыши дыра в форме четырехугольника.

Долетел змей до памятника того народа: “треугольной” башни. Разрушил и это здание. Раскололось здание на две половинки, а в месте их раскола остались треугольные дыры.

Поняли люди: нет сил это терпеть! Собрали межгалактические войска и победили дракона. А после восстанавливали город и удивлялись: как интересно были разрезаны здания.

Так что же делал дракон? Он разрезал геометрические тела, а на месте их разреза оставались сечения.

Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью.

Разумеется, никакой дракон не прилетает и не рассекает наши рисунки в тетради. Все сечения чертятся отдельно, а представляются мысленно.

Заметим, что в многогранниках сечение получается в форме многоугольника, вершины которого лежат на ребрах многогранника, а стороны на гранях

Обратим внимание, что две соседние вершины будут принадлежать одной и той же грани, то есть одной плоскости

Рассмотрим сечение пирамиды АВС: вершины А, В и С лежат точно на ребрах.

При этом пары вершин А и В, В и С, А и С лежат в одной грани и принадлежат одной плоскости.

Сечение геометрических тел является очень интересным разделом стереометрии. Поскольку это раздел стереометрии, в нем действуют все ее законы, в том числе и аксиомы стереометрии

В этой статье мы не будем заострять на них внимание, прочитать подробнее можно в статье «Аксиомы стереометрии. Расположение прямых и плоскостей в пространстве».

Зачем может потребоваться сечение? Мы сталкиваемся с ними намного чаще, чем думаем. Они бывают не только в задачах, но и встречаются в жизни.

Что мы делаем, когда нарезаем салат? Рассекаем овощи. Каждый разрез — это сечение.

А что делают архитекторы, когда чертят разрезы? Мысленно рассекают здание и показывают его “внутренности”.

Чем вода похожа на сечение?Посмотрим на бутылку с водой. Верхний уровень воды можно принять за плоскость, которая рассекает тело бутылки. Наклоняя бутылку и меняя положение воды, можно увидеть различные сечения, которые могут в ней появиться.

Сечения окружают нас, и в них совсем нет ничего сверхъестественного. А поэтому и разобраться в сечениях в стереометрии не составит для нас труда.

Как найти угол между прямой и плоскостью в пространстве

При решении задач используют один и следующих методов определения угла между прямой и плоскостью:

геометрический;
аналитический, также известный как алгебраический.

Рассмотрим алгоритм решения каждого из методов.

Суть геометрического способа ясна из его названия и заключается в построении чертежа, с помощью которого находят искомый угол. В трехмерной системе координат строят плоскость и заданную прямую. Из двух произвольно выбранных точек на прямой опускают перпендикуляры на плоскость. По точкам пересечения перпендикуляров с поверхностью проводят проекцию прямой. Допускается опускать перпендикуляр из одной точки прямой. В этом случае проекцию строят по точкам пересечения перпендикуляра и прямой с плоскостью.

После того как построена проекция прямой, решение задачи переходит в область планиметрии. Искомый угол находят через синус или косинус угла прямоугольного треугольника.

В аналитическом способе для вычисления искомого угла используют уравнения прямой и плоскости. Из уравнения прямой находят координаты ее направляющего вектора , а из уравнения плоскости – координаты нормального вектора . Тогда углом между плоскостью и прямой считают угол между векторами .

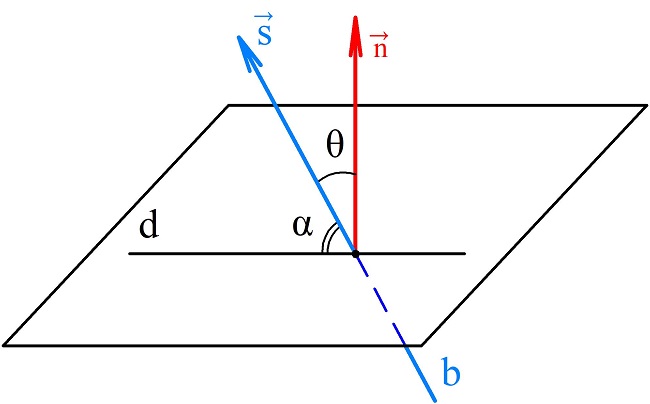
Косинус угла β можно найти через скалярное произведение векторов по формуле:

Угол . Подставим выражение для β в формулу косинуса, получим: .

Тогда синус искомого угла α можно определить следующим образом:

Плоскость: основное понятие

Основное понятие, связанное с плоскостью, — это уравнение плоскости. Уравнение плоскости позволяет определить все точки, которые находятся на ней. Оно задается в виде линейной комбинации трех координатных осей (x, y, z) с помощью коэффициентов a, b и c, и свободного члена d:

ax + by + cz + d = 0

Координаты точек, принадлежащих плоскости, удовлетворяют этому уравнению. Заметим, что если коэффициенты a, b и c равны нулю, то уравнение превращается в линию.

Основное понятие плоскости — это ее нормаль. Нормаль плоскости — это вектор, перпендикулярный к плоскости. Нормальные векторы могут быть положительно и отрицательно направлены, но для упрощения уравнения плоскости обычно выбираются нормальные векторы, указывающие в сторону положительных координат.

Плоскость может быть задана также через точку, через которую она проходит, и ее нормальный вектор. Это позволяет визуально представить плоскость и определить ее положение относительно других фигур и объектов.

Итак, плоскость — это двумерная геометрическая фигура в трехмерном пространстве, которая может быть определена уравнением или нормальным вектором. Она является важным понятием в геометрии и находит свое применение в различных областях, таких как физика, графика и архитектура.

Фактчек

Сечение — это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. При этом в многогранниках сечения представлены в виде многоугольников, вершины которых лежат на ребрах фигуры.
Существует несколько методов построения сечения в многогранниках: метод следов, метод внутреннего проектирования и комбинированный метод.
Метод следов заключается в том, что по следу сечения можно построить его полностью. След сечения — прямая, по которой секущая плоскость пересекает грань многогранника. В методе следов часто нужно продлевать линии и ребра до их пересечения.
Метод внутреннего проектирования позволяет параллельно переносить сторону сечения в параллельных плоскостях. Это может быть удобно в случаях, когда метод следов невозможно или трудно применить.
Комбинированный метод — метод, который сочетает в себе и метод следов, и метод внутреннего проектирования.

Что такое плоскость, проходящая через прямую: объяснение и примеры

Подобно прямым, плоскости обозначают буквами латинского алфавита, например, плоскость ABС или плоскость P. Прямая, через которую проходит плоскость, называется прямой-носитель плоскости.

Для определения плоскости, проходящей через прямую, необходимо задать еще одну точку, не совпадающую с прямой. Эта точка будет определять направление и наклон плоскости. Таким образом, для полного описания плоскости, проходящей через прямую, необходимо указать прямую-носитель и одну дополнительную точку.

Примеры:

Рассмотрим прямую AB и точку C, не лежащую на прямой. Плоскость, проходящая через прямую AB и точку C, можно обозначить как плоскость ABC или плоскость P.
Если прямая AB совпадает с носителем плоскости, то для определения плоскости достаточно указать эту прямую и любую дополнительную точку D, не лежащую на ней.
Если задано две пересекающиеся прямые, то плоскость, проходящая через эти прямые, можно обозначить их общими точками, например, плоскость ABD или плоскость P.

Итак, плоскость, проходящая через прямую, — это плоская поверхность, содержащая заданную прямую и другие точки, определяющие ее направление и наклон. Задается такая плоскость с помощью прямой-носителя и одной дополнительной точки.

Способы задания плоскости

В геометрии существует несколько способов задания плоскости. Рассмотрим основные из них:

Геометрический способ: плоскость можно задать с помощью трех своих непараллельных прямых, плоскость проходит через все три прямых одновременно.
Аналитический способ: задание плоскости может быть осуществлено с помощью уравнения плоскости в пространстве. Уравнение плоскости имеет вид Ax + By + Cz + D = 0, где A, B, C — коэффициенты, определяющие нормаль к плоскости, а D — свободный член.
Векторный способ: плоскость можно задать с помощью двух перпендикулярных прямых в плоскости. Также можно задать плоскость с помощью ее нормали и точки, через которую она проходит.

Выбор способа задания плоскости зависит от конкретной задачи и предпочтений геометра. Каждый из способов имеет свои преимущества и подходит для определенных геометрических конструкций.

Пучок прямых.

Пучком прямых на плоскости называется множество прямых, проходящих через фиксированную точку — центр пучка. Пусть $A_{1}x+B_{1}y+C_{1}=0$ и $A_{2}x+B_{2}y+C_{2}=0$ — уравнения двух прямых, принадлежащих пучку. Тогда уравнение
$$
\alpha(A_{1}x+B_{1}y+C_{1})+\beta(A_{2}x+B_{2}y+C_{2})=0\label{ref13}
$$
при условии $\alpha^{2}+\beta^{2} \neq 0$ называется уравнением пучка прямых.

Основанием для этого служит следующее утверждение.

Утверждение 3.

При любых $\alpha$ и $\beta$ $(\alpha^{2}+\beta^{2} \neq 0)$ уравнение \eqref{ref13} определяет прямую линию, принадлежащую пучку. Обратно, уравнение каждой прямой из пучка представимо в виде \eqref{ref13}.

Докажем сначала, что коэффициенты при переменных в уравнении \eqref{ref13} не равны нулю одновременно. Для этого перепишем его в виде
$$
(\alpha A_{1}+\beta A_{2})x+(\alpha B_{1}+\beta B_{2})y+(\alpha C_{1}+\beta C_{2})=0.\nonumber
$$
Допустим, что $\alpha A_{1}+\beta A_{2}=0$ и $\alpha B_{1}+\beta B_{2}=0$. Так как прямые пересекаются, $A_{1}B_{2}-A_{2}B_{1} \neq 0$ и , что значения $\alpha=0$, $\beta=0$ единственные, которые удовлетворяют этим двум равенствам. Но эти значения мы исключили. Таким образом, уравнение \eqref{ref13} определяет прямую линию.

Обозначим через $x_{0}$, $y_{0}$ координаты центра пучка. По условию
$$
A_{1}x_{0}+B_{1}y_{0}+C_{1}=0,\ A_{2}x_{0}+B_{2}y_{0}+C_{2}=0,\nonumber
$$
а потому $x_{0}$, $y_{0}$ удовлетворяют уравнению \eqref{ref13}, и прямая проходит через центр пучка.

Вторая часть предложения будет доказана, если окажется, что через любую точку, отличную от центра пучка $M_{0}$, проходит прямая линия с уравнением вида \eqref{ref13}. Легко проверить, так ли это. Рассмотрим точку $M_{1}(x_{1}, y_{1})$, отличную от $M_{0}$, и обозначим
$$
u=A_{1}x_{1}+B_{1}y_{1}+C_{1}=0,\ v=A_{2}x_{1}+B_{2}y_{1}+C_{2}=0\nonumber
$$
Так как наши прямые имеют только одну общую точку, числа $u$ и $v$ одновременно не равны нулю, и мы вправе положить $\alpha=-v$, $\beta=-u$. При таких значениях $\alpha$ и $\beta$ координаты точки $M_{1}$ удовлетворяют уравнению \eqref{ref13}. Это означает, что соответствующая этим значениям прямая пучка проходит через $M_{1}$, и утверждение доказано.

Заметим, что каждая пара чисел $\alpha$ и $\beta$ $(\alpha^{2}+\beta^{2} \neq 0)$ определяет в пучке единственную прямую, но каждой прямой соответствуют бесконечно много пропорциональных между собой пар чисел.

Если нам известны координаты центра пучка, то уравнение пучка можно написать в виде
$$
\alpha(x-x_{0})+\beta(y-y_{0})=0,\nonumber
$$
положив, что пучок определяется прямыми $x-x_{0}=0$ и $y-y_{0}=0$. Впрочем, и без того очевидно, что это — уравнение произвольной прямой, проходящей через $M_{0}$.

Систему из уравнений прямых, определяющих пучок, можно рассматривать как уравнение центра пучка. Поэтому уравнение каждой прямой пучка есть следствие этой системы. Теперь наш результат можно сформулировать так.

Утверждение 4.

Если система линейных уравнений имеет решение., то некоторое линейное уравнение является ее следствием тогда и только тогда, когда оно есть сумма уравнений системы, умноженных на какие-то числа.

Мы доказали это предложение для частного случая систем из двух уравнений с двумя неизвестными. В общем виде оно вытекает из результатов главы о системах линейных уравнений. Другими геометрическими интерпретациями этого предложения являются пучки и связки плоскостей.

Пучком плоскостей называется множество плоскостей, проходящих через фиксированную прямую — ось пучка. Уравнение пучка плоскостей имеет вид
$$
\alpha(A_{1}x+B_{1}y+C_{1}z+D_{1})+\beta(A_{2}x+B_{2}y+C_{2}z+D_{2})=0,\nonumber
$$
где $\alpha^{2}+\beta^{2} \neq 0$, а в скобках стоят левые части уравнений двух различных плоскостей пучка.

Связкой плоскостей называется множество плоскостей, проходящих через фиксированную точку — центр связки. Уравнение связки плоскостей имеет вид
$$
\alpha(A_{1}x+B_{1}y+C_{1}z+D_{1})+\beta(A_{2}x+B_{2}y+C_{2}z+D_{2}) +\\+ \gamma(A_{3}x+B_{3}y+C_{3}z+D_{3})=0,\nonumber
$$
где $\alpha^{2}+\beta^{2}+\gamma^{2} \neq 0$, а в скобках стоят левые части уравнений плоскостей связки, имеющих центр своей единственной общей точкой.

О геометрическом смысле порядка алгебраической линии.

Предположим, что на плоскости дана алгебраическая линия $L$, имеющая в декартовой системе координат уравнение
$$
A_{1}x^{k_{1}}y^{l_{1}}+…+A_{s}x^{k_{s}}y^{l_{s}}=0.\label{ref14}
$$
Рассмотрим произвольную прямую с параметрическими уравнениями
$$
x=x_{0}+a_{1}t,\ y=y_{0}+a_{2}t.\label{ref15}
$$
Найдем точки пересечения $L$ и прямой линии. Они будут известны, если мы найдем соответствующие им значения параметра $t$. Это будут те значения, при которых $x$ и $y$, выраженные по формулам \eqref{ref15}, удовлетворяют уравнению \eqref{ref14}. Подставим \eqref{ref15} в \eqref{ref14}:
$$
A_{1}(x_{0}+a_{1}t)^{k_{1}}(y_{0}+a_{2}t)^{l_{1}}+…+A_{s}(x_{0}+a_{1}t)^{k_{s}}(y_{0}+a_{2}t)^{l_{s}}=0.\label{ref16}
$$
Раскрывая скобки в каждом члене, мы получим многочлены относительно $t$ степеней $k_{1}+l_{1}, …, k_{s}+l_{s}$. Их сумма будет многочленом, степень которого не выше, чем максимальная из степеней слагаемых. Но максимальное из чисел $k_{1}+l_{1},…,k_{s}+l_{s}$ — это порядок линии $L$. Поэтому степень уравнения \eqref{ref16} не превосходит порядка линии.

Может, конечно, случиться, что все коэффициенты этого уравнения равны нулю, и оно представляет собой тождество. Если исключить этот случай, то число корней уравнения и, следовательно, число точек пересечения не превосходит порядка линии. Таким образом, мы доказали следующее утверждение.

Утверждение 5.

Число точек пересечения алгебраической линии с прямой, которая на ней не лежит целиком, не превосходит порядка линии.

Существуют линии, которые ни с одной прямой не имеют в принципе возможного числа точек пересечения, равного порядку линии. Примерами могут служить линии с уравнениями $x^{2}+y^{2}=0$ или $(x^{2}+y^{2})^{2}-1=0$.

Пример.

Архимедова спираль — линия с уравнением $r=\alpha\varphi$ в полярной системе координат — пересекает каждую прямую, проходящую через полюс, в бесконечном числе точек. Следовательно, она не является алгебраической линией.

Свойства угла между прямой и плоскостью в пространстве

Приведем основные свойства угла между прямой и плоскостью:

Из точки пересечения прямой и плоскости построим перпендикуляр к плоскости. Так как прямая, ее проекция и перпендикуляр лежат в одной плоскости, можно утверждать, что угол между прямой и плоскостью дополняет до 90° угол между перпендикуляром и прямой.
Если угол между прямой и плоскостью равен 0º, то прямая параллельна плоскости. Если угол между прямой и плоскостью равен 90º, прямая является перпендикуляром к плоскости.
Перпендикуляр к плоскости всегда меньше по величине чем наклонная, проведенная из той же плоскости.
Проекции двух равных наклонных, проведенных из одной точки, также равны между собой.

К свойствам угла между прямой и плоскостью можно отнести свойства линий, образующих данный угол: наклонной, проекции.

Сформулируем теорему о трех перпендикулярах и докажем ее.

Доказательство

Через точку пересечения наклонной MK и плоскости φ проведем прямую f. Теперь построим отрезок LK так, что LK||MN. Отрезок так как перпендикулярен плоскости, в которой лежит f. По двум параллельным отрезкам LK и MN построим плоскость . Тогда f перпендикулярна NK и LK, а значит, и плоскости ω. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, принадлежащей этой плоскости, то есть , что и требовалось доказать.

Свойства плоскости, проходящей через прямую

Плоскость, проходящая через прямую, имеет ряд свойств, которые можно использовать для анализа и решения геометрических задач. Вот некоторые из них:

Вся плоскость проходит через каждую точку прямой. Получается, что прямая является частью плоскости, а все точки прямой лежат в этой плоскости.
Любые две различные плоскости, проходящие через прямую, могут быть параллельными или пересекающимися. В зависимости от положения прямой относительно плоскостей, возможны различные варианты их взаимного расположения.
Если две плоскости проходят через одну и ту же прямую, то они называются скрещивающимися плоскостями. Это означает, что плоскости пересекаются между собой и не являются параллельными.
Прямая, которая лежит в плоскости, называется прямой, лежащей в плоскости. Все точки этой прямой также лежат в плоскости.
Если прямая параллельна одной плоскости, проходящей через неё, то она параллельна и всем другим плоскостям, проходящим через эту прямую.

Эти свойства плоскости, проходящей через прямую, позволяют упростить геометрические задачи и установить связи между прямыми и плоскостями в пространстве.

Уравнение для плоскости, которая проходит через 3 точки

Если 3-мерном пространстве дана прямоугольная к-ная система, она обозначена обычно Oxyz.

Тогда уравнение, где данные a, b и C являются действительными числами больше нуля, именуется ур-ем плоскости на отрезки.

При абсолютном значении чисел a, b и с, они будут равны длине отрезков, обрезанных плоскостью по осям координат. Буквенные значения демонстрируют положительное или отрицательное направление линейных сегментов относительно оси координат.

Чтобы составить общее уравнение для исходной плоскости, можно применить следующую теорему.

Теорема:

Любое уравнение, имеющее стандартный вид, имеет действительные значения A, b, C и D, которые не должны быть равны нулю. Эти данные определяют исходную плоскость в системе координат Oxyz, расположенной в 3-мерном пространстве.

Эта теорема содержит в себе 2 части:

Сначала получаем общее уравнение для плоскости, которая будет проходить через точку и саму плоскость.
Затем мы доказываем, что данное уравнение можно использовать для действительных чисел, чтобы доказать, что оно будет определять плоскость V, Z и D.

Доказательство 1 части:

Так как значения чисел A, V и Z не будут равны нулю одновременно, значит есть определенная точка, координаты которой будут соответствовать исходному уравнению, то есть выдавать верное равенство.
Далее вычитаем правую и левую части полученного уравнения из данного уравнения. Получается уравнение, которое будет эквивалентно исходному.
Далее необходимо будет доказать, что полученное уравнение будет определять именно плоскость в данной системе координат 3-мерного пространства и найти общее уравнение.

Главным условием для перпендикулярности 2 векторов является их равенство. То есть, когда координаты удовлетворяют уравнению, то векторы будут перпендикулярны и наоборот. При верном равенстве набор точек будет обуславливать плоскость, проходящую через эту точку.

Полученное уравнение будет определять плоскость, расположенную в 3-мерном пространстве. Также оно будет полностью соответствовать для общего уравнения плоскости, которая проходит через три точки.

Из сказанного следует, что любое уравнение, эквивалентное исходному, будет определять одну и ту же плоскость. Мы доказали 1 часть теоремы.

Доказательство 2 части теоремы:

Когда имеем плоскость, проходящую через точку, вектор которой нормален, мы можем доказать, что в прям-ной координатной системе Oxyz ее задают с помощью данного основного уравнения.

Если взять любую точку данной системы координат, то векторы будут перпендикулярны, а произведение будет равно нулю.

После принятия данного понятия, уравнение снова изменится и будет определять нашу плоскость.

Вывод: если уравнения эквивалентны, то они определяют одинаковую плоскость. Мы доказали теорему.

Данный обзор будет полезен при решении математических задач, а также в аналитической геометрии.