Tan в математике: что это такое и как использовать

Содержание

Геометрическое определение

Тригонометрические функции обычно определяются геометрически. Пусть будет декартова система координат на плоскости и окружность радиуса R с принципом O в качестве центра. Пусть угол измеряется как поворот от положительного направления горизонтальной оси к лучу OB. Направление против часовой стрелки является положительным, а направление по часовой стрелке — отрицательным. Обозначим через x_B и покажем его упорядоченным по y_B (см. рис.)

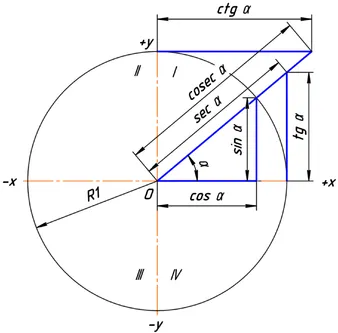
Рис. 3. Тригонометрические функции угла α с радиусом, равным 1.

Благодаря схожим свойствам формы, очевидно, что значение тригонометрической функции не зависит от радиуса окружности R. Во многих случаях этот радиус принимается равным значению единичного отрезка, а синусоида — это просто прямой угол y._B Синус — это отклонение x_B. На рисунке 3 показана величина тригонометрической функции единичного круга.

Когда a вещественно, синус a в математическом анализе — это синус угла, радиальное измерение которого равно a, как и для других тригонометрических функций.

Определение тригонометрических функций для острых углов

Во многих предыдущих учебниках по геометрии тригонометрическая функция острого угла определяется как отношение сторон прямоугольного треугольника. Пусть OAB — треугольник с углом a. Итак.

Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)

Постройте систему координат, используя направление ребер линий вдоль начала координат O и OA, при необходимости измените направление (инверсия) треугольника и поместите его в первую четверть системы координат, затем постройте окружность. Для радиуса, равного косой грани, сразу видно, что определение этой функции дает тот же результат, что и предыдущее определение. Это определение имеет ряд педагогических преимуществ, так как не требует введения понятия системы координат, но имеет и серьезный недостаток: нельзя определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении базовых задач. тупоугольные треугольники (см. теорема о полутонах, теорема о коэффициентах).

Определение тригонометрических функций как решений дифференциальных уравнений

Функции косинуса и полутона можно определить как четные (полутон) и нечетные (синус) решения дифференциальных уравнений.

R(\varphi) = — R(\varphi),» width=»» height=»» />

Если начальное условие cos(0) = sin'(0) = 1, то есть производная второго порядка берется как функция переменной, равной самой функции, со знаком минус.

Функции кокерина и синуса можно определить как непрерывные решения (f и g соответственно) системы интересных уравнений: f(x+y)& amp; amp; f(x)f(y)-g(x(x))-g(y) g(x+y)& amp; amp; «width =» «height =» » />

Тангенс

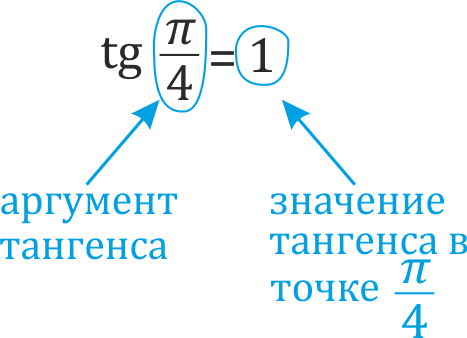
Аргументом тангенса может быть: — как число или выражение с Пи: \(1,3\), \(\frac\), \(π\), \(-\frac\) и т.п. — так и угол в градусах: \(45^°\), \(360^°\),\(-800^°\), \(1^° \) и т.п.

Для обоих случаев тангенс вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).

Тангенс острого угла

1) Пусть дан угол и нужно определить тагенс этого угла.

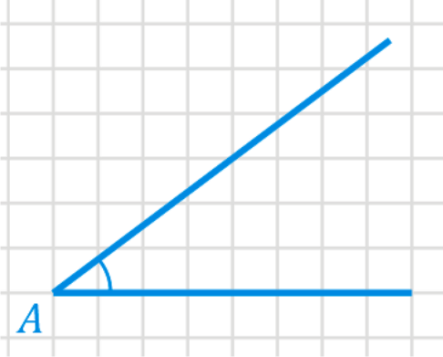
2) Достроим на этом угле любой прямоугольный треугольник.

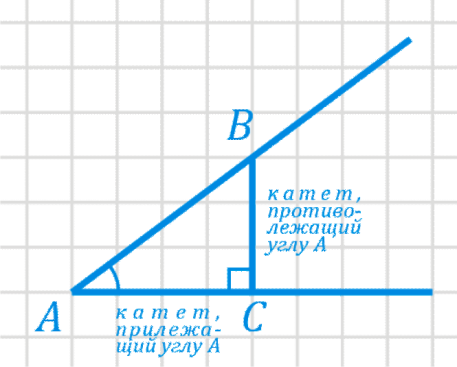
3) Измерив, нужные стороны, можем вычислить тангенс.

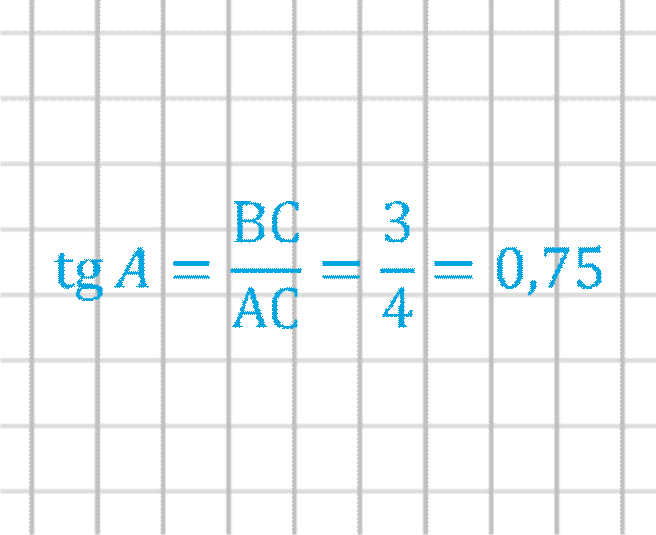
Вычисление тангенса числа или любого угла

Пример. Вычислите \(tg\:0\). Решение: Чтобы найти тангенс нуля нужно найти сначала синус и косинус \(0\). И то, и другое найдем с помощью тригонометрического круга :

Точка \(0\) на числовой окружности совпадает с \(1\) на оси косинусов, значит \(cos\:0=1\). Если из точки \(0\) на числовой окружности провести перпендикуляр к оси синусов, то мы попадем в точку \(0\), значит \(sin\:⁡0=0\). Получается: \(tg\:0=\) \(\frac\) \(=\) \(\frac\) \(=0\).

Пример. Вычислите \(tg\:(-765^\circ)\). Решение: \(tg\: (-765^\circ)=\) \(\frac\) Что бы вычислить синус и косинус \(-765^°\). Отложим \(-765^°\) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на \(720^°\) , а потом еще на \(45^°\).

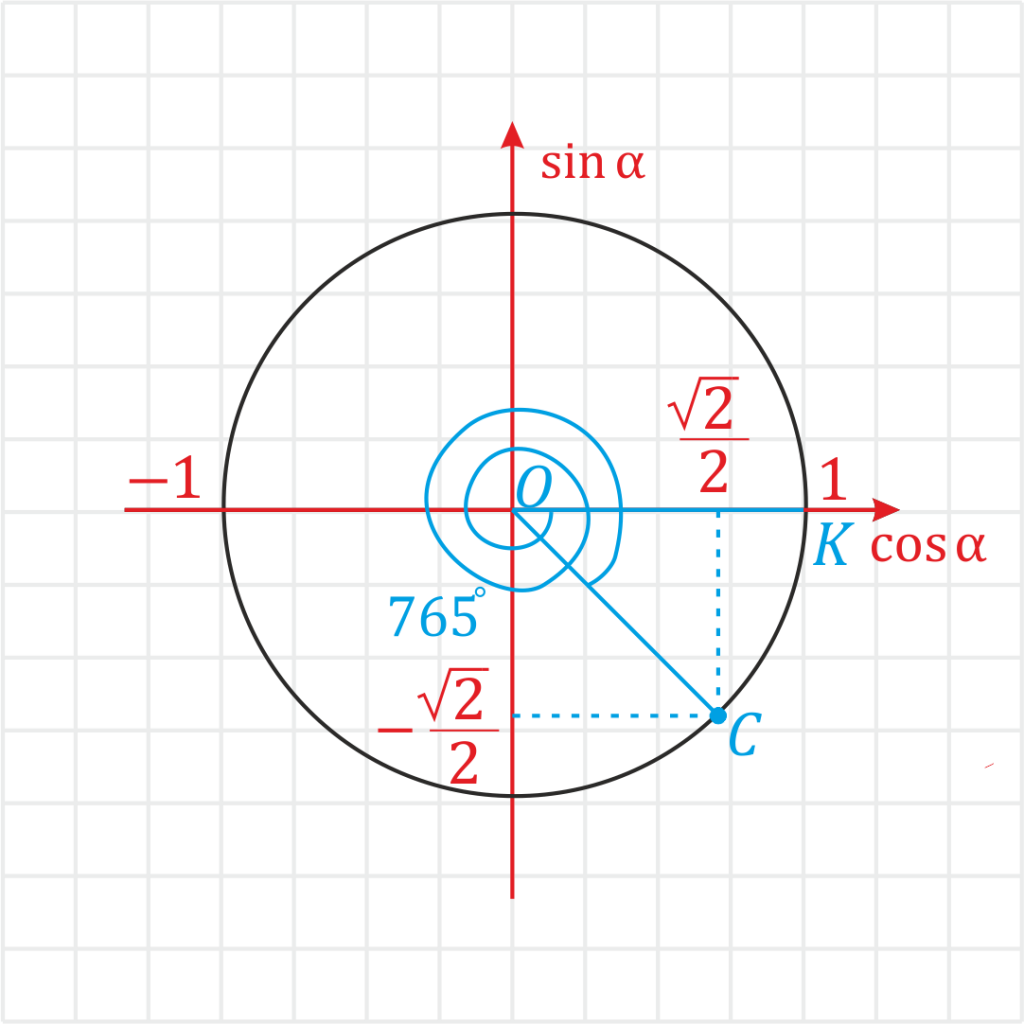
Однако можно определять тангенс и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:

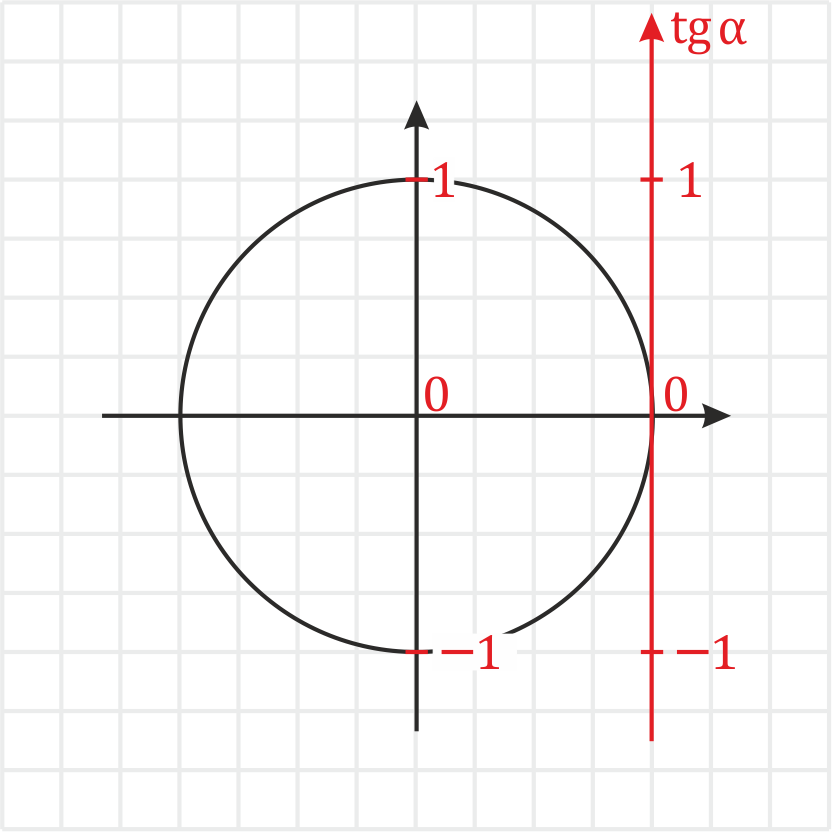
Ось тангенсов – это фактически копия оси синусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси синусов.

Чтобы определить тангенс с помощью числовой окружности, нужно: 1) Отметить соответствующую аргументу тангенса точку на числовой окружности. 2) Провести прямую через эту точку и начало координат и продлить её до оси тангенсов. 3) Найти координату пересечения этой прямой и оси тангенсов.

Пример. Вычислите \(tg\:\frac\). Решение: 1)Отмечаем \(\frac\) на окружности.

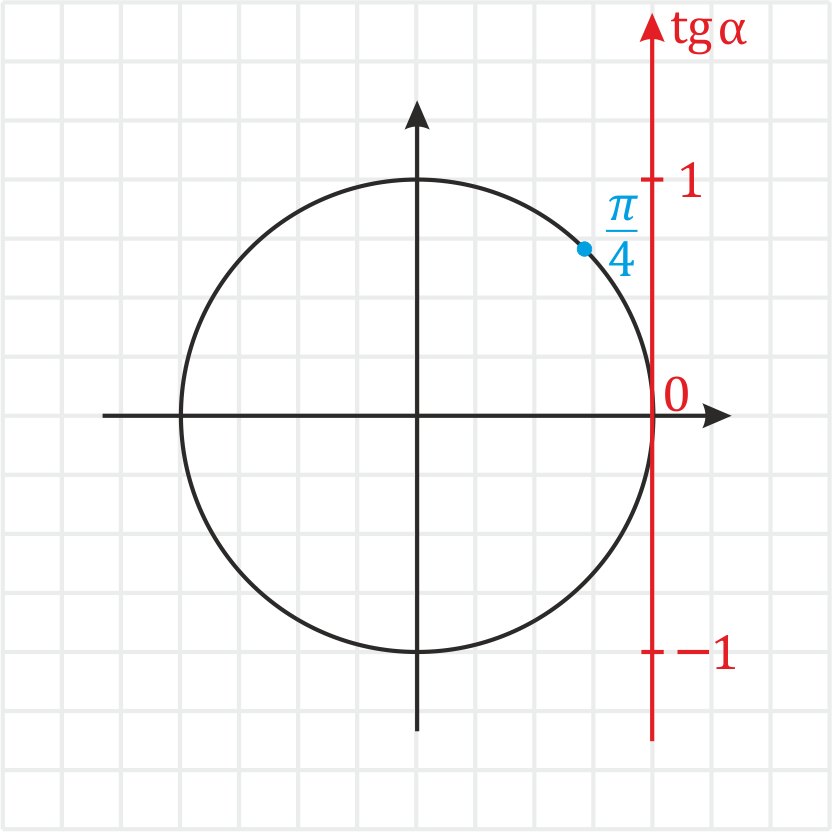
2) Проводим через данную точку и начало координат прямую.

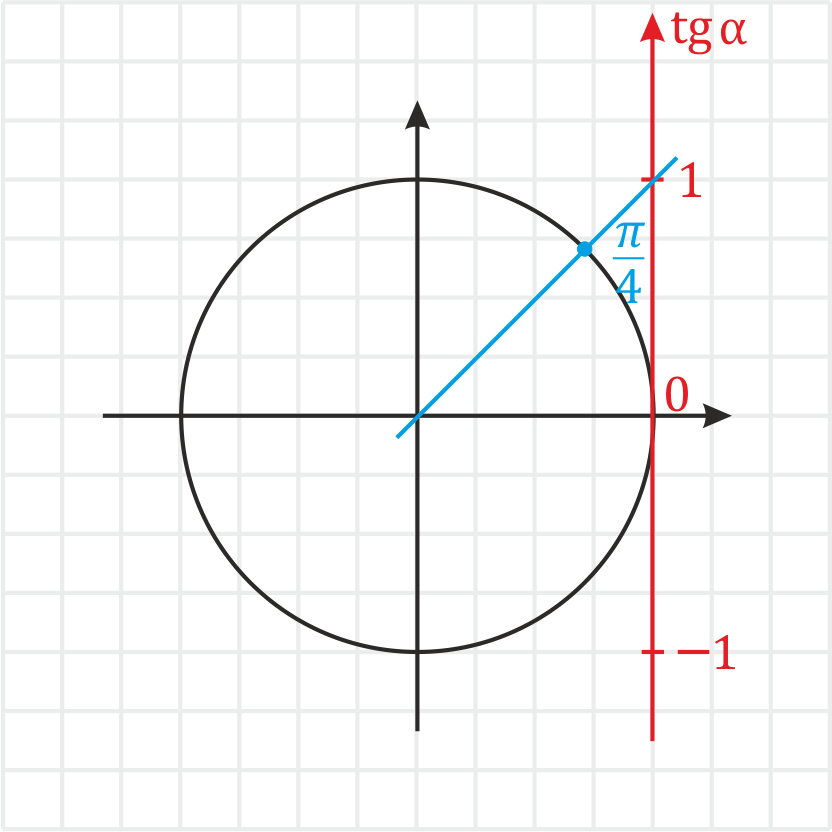
3) В данном случае координату долго искать не придется – она равняется \(1\).

Пример. Вычислите \(tg\: 45°\) и \(tg\: (-240°)\). Решение: Для угла \(45°\) (\(∠KOA\)) тангенс будет равен \(1\), потому что именно в таком значении сторона угла, проходящая через начало координат и точку \(A\), пересекает ось тангесов. А для угла \(-240°\) (\(∠KOB\)) тангенс равен \(-\sqrt\) (приблизительно \(-1,73\)).

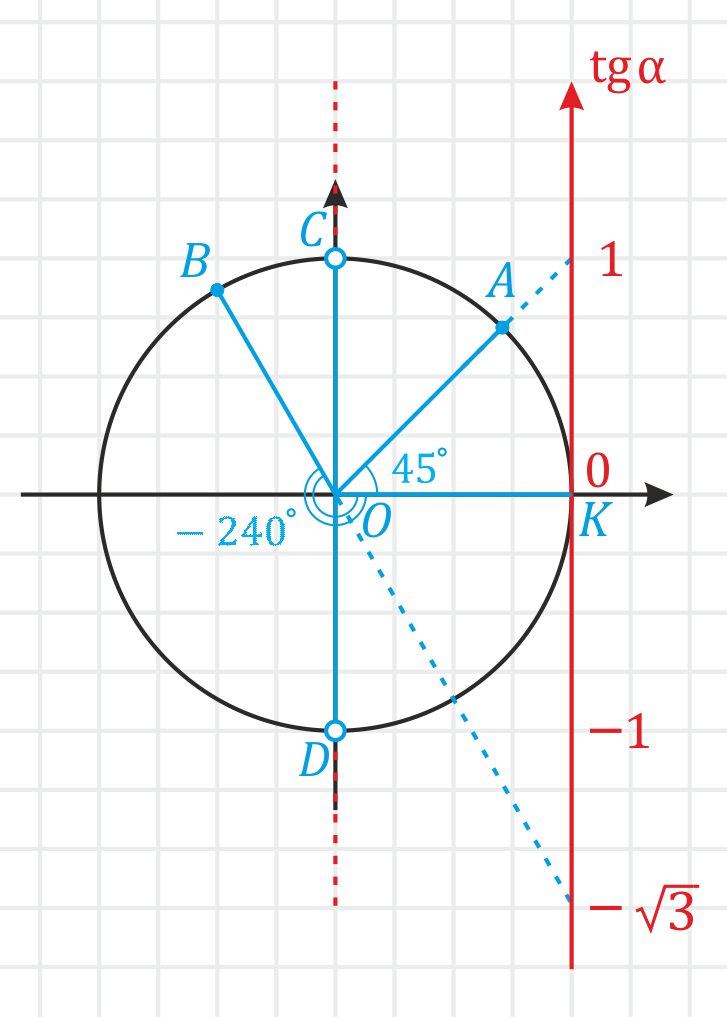
Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.

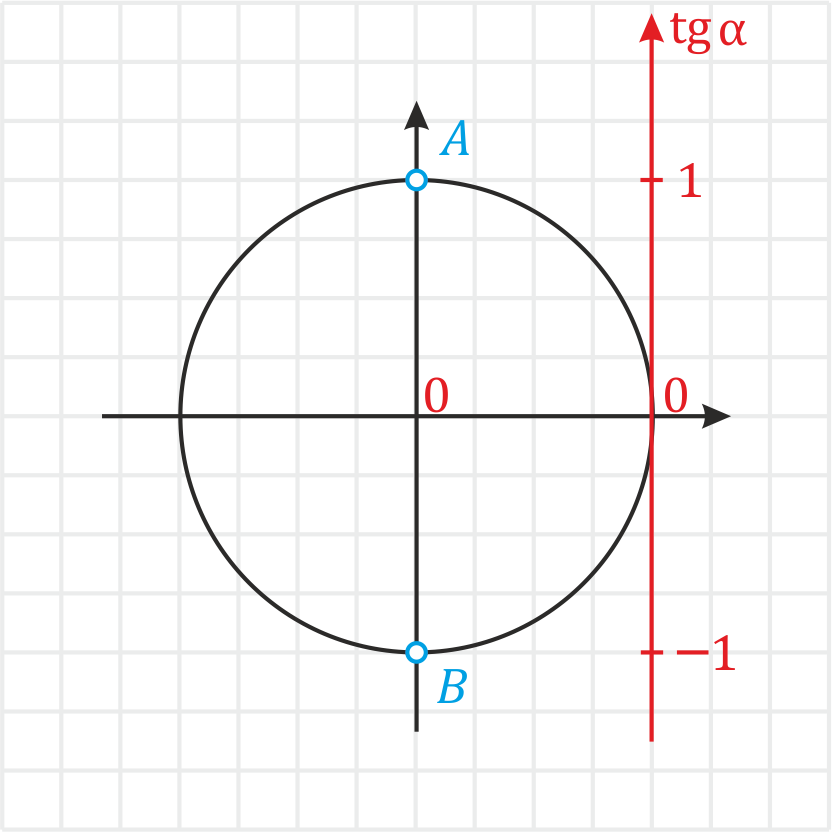
При этом тангенс не определен для: 1) всех точек \(A\) (значение в Пи: …\(-\) \(\frac\) ,\(-\) \(\frac\) , \(\frac\) , \(\frac\) , \(\frac\) …; и значение в градусах: …\(-630°\),\(-270°\),\(90°\),\(450°\),\(810°\)…) 2) всех точек \(B\) (значение в Пи: …\(-\) \(\frac\) ,\(-\) \(\frac\) ,\(-\) \(\frac\) , \(\frac\) , \(\frac\) …; и значение в градусах: …\(-810°\),\(-450°\),\(-90°\),\(270°\)…) .

Так происходит потому, что прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось тангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках тангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений тангенс может быть найден).

Из-за этого при решении тригонометрических уравнений и неравенств с тангенсом необходимо учитывать ограничения на ОДЗ .

Знаки по четвертям

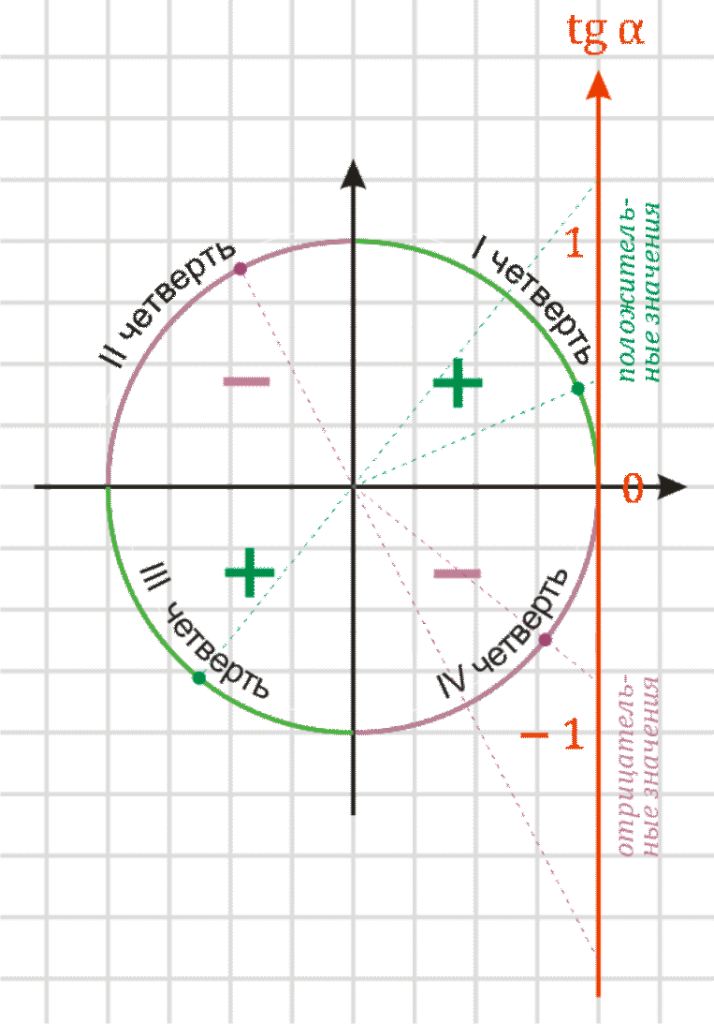
С помощью оси тангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак тангенса для нее описанным выше способом. У всей четверти знак будет такой же.

Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение тангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение тангенса будет положительно (знак плюс). С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

— котангенсом того же угла: формулой \(ctg⁡\:x=\) \(\frac\) Другие наиболее часто применяемые формулы смотри здесь .

Тангенс по градусам: подробное объяснение и примеры

Формула для вычисления тангенса по градусам: тангенс (α) = противоположная сторона / прилежащая сторона;

Градусы — это единицы измерения угла. Один полный оборот составляет 360 градусов. Для вычисления тангенса по градусам необходимо знать значения противоположной и прилежащей сторон треугольника. Противоположная сторона — это сторона, лежащая напротив угла, а прилежащая сторона — это смежная к углу сторона.

Для лучшего понимания работы тангенса по градусам, рассмотрим пример.

Пример: Допустим, у нас есть прямоугольный треугольник со сторонами противоположной стороны равной 5 и прилежащей стороны равной 3. Чтобы найти тангенс угла α, мы должны разделить длину противоположной стороны на длину прилежащей стороны. В этом случае, тангенс α = 5/3.

Таким образом, нахождение тангенса по градусам требует знания значений противоположной и прилежащей сторон прямоугольного треугольника, а затем применение соответствующей формулы. Это позволяет определить отношение противоположной стороны и прилежащей стороны, что является основной задачей тангенса.

Тангенс и котангенс: определение и свойства

Тангенс угла определяется как отношение противолежащей стороны к прилежащей стороне треугольника. Обозначается как tg или tan. Формула для вычисления тангенса: tg(A) = a/b, где A — угол, а a и b — стороны треугольника.

Котангенс угла — это обратное значение тангенса. Он определяется как отношение прилежащей стороны к противолежащей стороне треугольника. Котангенс обозначается как ctg или cot. Формула для вычисления котангенса: ctg(A) = b/a.

Свойства тангенса и котангенса:

Значение тангенса лежит в диапазоне от минус бесконечности до плюс бесконечности.
Значение котангенса лежит в диапазоне от минус бесконечности до плюс бесконечности.
Значение тангенса и котангенса зависит от угла и может быть положительным или отрицательным.
Значение тангенса и котангенса повторяется с периодом в 180 градусов или π радиан.
Тангенс и котангенс являются взаимно обратными функциями друг друга.

Тангенс и котангенс широко используются в геометрии, физике, инженерии и других научных дисциплинах для решения задач связанных с треугольниками, углами и прямыми.

Тангенс: определение и свойства

Основные свойства тангенса:

Тангенс определяется только для углов в прямоугольном треугольнике.
Значение тангенса нельзя выразить через значения синуса и косинуса.
Значения тангенса могут быть положительными или отрицательными, в зависимости от квадранта, в котором находится угол.
Тангенс угла с нулевым тангенсом равен нулю.
Тангенс угла с бесконечным тангенсом не определен.

Тангенс обладает следующими свойствами:

Тангенс угла равен отношению синуса угла к косинусу угла: .
Тангенс угла меняет своё значение при переходе через угол, равный 180 градусов или π радиан.
Периодический характер тангенса: тангенс угла повторяет свои значения с периодом 180 градусов или π радиан.
Тангенс угла увеличивается от нуля до бесконечности при движении угла от 0 до 90 градусов или от 0 до π/2 радиан.
Тангенс отрицательного угла равен отрицательному значению тангенса положительного угла такой же меры: .

Котангенс: определение и свойства

Обозначение котангенса угла θ:

Котангенс также может быть определен как отношение косинуса угла к синусу угла:

Свойства котангенса:

Значение котангенса всегда отрицательно, кроме точек, где тангенс равен нулю, и известно, что котангенс θ = -cot(θ).
Периодичность: котангенс периодичен с периодом π, то есть , где n — целое число.
Котангенс угла в прямоугольном треугольнике может быть выражен как отношение длины прилежащего катета к длине противолежащего катета.
Котангенс угла отвечает за отношение по горизонтали и вертикали, отрицательное значение обозначает, что две стороны противоположны друг другу.
Котангенс функции периодичен с периодом π, что отражается на графике функции.

Калькуляторы и электронные устройства

Калькуляторы и электронные устройства широко применяются для вычислений тангенса и других тригонометрических функций. Современные калькуляторы, как физические, так и программные, обычно имеют встроенную функцию вычисления тангенса, а также других тригонометрических функций, что делает их очень удобными для работы с этими функциями.

Калькуляторы могут иметь различные клавиши для ввода угла в градусах или радианах, и клавишу для вычисления тангенса. После ввода угла калькулятор выдает значение тангенса на дисплее. В программных калькуляторах такая функция также доступна с помощью соответствующего меню или команды.

Кроме калькуляторов, существует множество других электронных устройств, которые могут вычислять тангенс. Например, это могут быть электронные счетчики, компьютеры, смартфоны и другие портативные устройства. Многие из них имеют встроенные калькуляторы, что позволяет с легкостью решать задачи, связанные с тангенсом и другими тригонометрическими функциями.

Устройство	Описание	Преимущества
Физический калькулятор	Портативное устройство с клавишами и дисплеем для вычислений	Удобство использования вне компьютерной среды
Программный калькулятор	Приложение на компьютере или смартфоне для вычислений	Возможность использования на различных устройствах
Электронный счетчик	Устройство для измерения электрических параметров	Высокая точность измерений тангенса
Компьютер	Устройство для обработки и хранения данных	Возможность использования специализированных программ для вычисления тангенса
Смартфон	Мобильное устройство с широкими возможностями	Портативность и простота использования

С использованием калькуляторов и электронных устройств, вычисление тангенса становится проще и быстрее

Они позволяют получать точные значения функции, что особенно важно при решении различных математических задач

Отрицательный тангенс: определение и свойства

Отрицательный тангенс может быть определен как отношение сторон треугольника, где противоположная сторона отрицательна, а прилежащая сторона положительна.

Свойства отрицательного тангенса:

Значение отрицательного тангенса находится в промежутке от минус бесконечности до нуля, не включительно.
Значение отрицательного тангенса равно нулю в точках, где противоположная сторона равна нулю, а прилежащая сторона отрицательна.
Значение отрицательного тангенса меняется с приростом или убыванием угла, и его график имеет периодичность, повторяющуюся каждые 180 градусов.
Отрицательный тангенс может быть использован для нахождения угла треугольника, зная значения противоположной и прилежащей сторон.

Отрицательный тангенс играет важную роль в различных областях, таких как физика, инженерия и математика. Он используется для решения задач, связанных с треугольниками и углами. Понимание его определения и свойств позволяет более эффективно решать такие задачи.

Общая информация

Раздел математики, который занимается изучением тригонометрических функций, называется тригонометрией. К функциям относятся следующие: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существуют также и обратные им функции: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg).

Для нахождения знаков тригонометрических функций по четвертям рекомендуется применять специальный «инструмент». Он называется окружностью синусов и косинусов. Однако по ней можно находить не только функции, которые соответствуют ее названию, но и другие. Делается это с помощью тригонометрических тождеств.

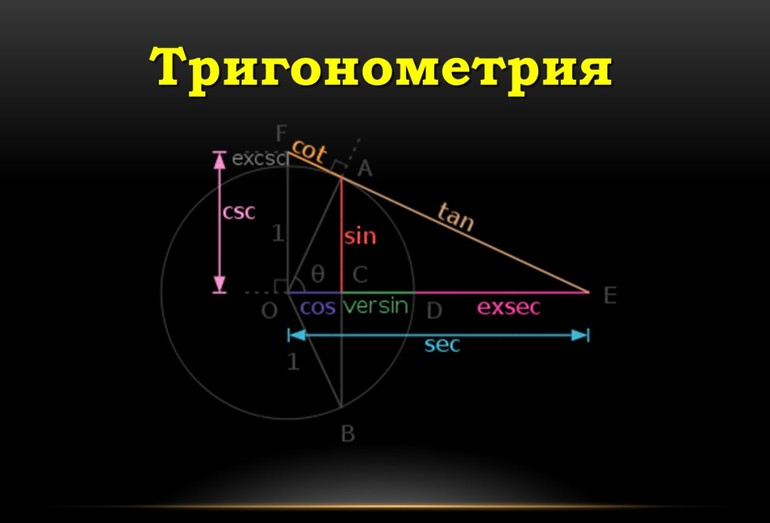
Виды углов

Важной «ступенью» в освоении тригонометрии является идентификация углов. Они делятся на 7 видов

Кроме того, существует еще два типа классификации по знаку: положительные и отрицательные.

Для составления критериев, по которым математики классифицируют углы, необходимо ввести некоторую переменную. Пусть существует некоторый угол a, градусная мера которого составляет x градусов. Необходимо рассмотреть 7 случаев, в которых он измеряется только в градусной размерности:

При х < 90 угол считается острым.
Если х = 90, то является прямым.
В случае, когда выполняется неравенство, он считается тупым: 90 < x < 180.
Развернутый: х = 180.
Выпуклый: 180 < x < 360.
Полный: х = 360.
Свыше 360: x > 360.

Градус — это не единственная единица измерения размерности угла. Существует также и радиан, который пользуется большей популярностью, чем предыдущая единица. Согласно статистике, которая составлена математиками, при решении задач с тригонометрическим уклоном многие используют радиан (около 95,88%). Это объясняется удобством, поскольку в основном применяется тригонометрическая окружность для быстрого нахождения значений функций. Перевод одной единицы в другую осуществляется с помощью двух простых соотношений:

В радианы: P = (a * ПИ) / 180.
В градусы: а = (P * 180) / ПИ.

Существует 2 метода перевода: автоматизированный и ручной. В первом случае следует применять специальные радианные таблицы, программы и тригонометрическую окружность. Во втором — пользоваться формулами для преобразований. Если очень часто приходится решать задачи подобного типа, то можно создать свой инструмент. Для этого потребуется табличный процессор EXCEL. Необходимо вбить в ячейки две формулы, и тогда ручной метод «превратится» в автоматизированный.

Смысл функций

Тригонометрические функции используются не только в математике, но и в других дисциплинах (физике, электронике, микросхемотехнике, акустике и так далее). С их помощью можно описывать законы изменения различных периодических величин.

Синус угла — значение, которое вычисляется отношением линейного размера противолежащего катета к гипотенузе прямоугольного треугольника. Если выразить величину через отношение прилежащего катета к гипотенузе, то она называется косинусом угла. Величина, полученная при отношении двух катетов — противолежащего к прилежащему, называется тангенсом. В случае с котангенсом, необходимо поменять числитель и знаменатель местами, то есть отношение прилежащего к противолежащему. Следует также напомнить, что все четыре функции обладают периодичностью. Для sin и cos период соответствует 2 ПИ, а для tg и ctg — ПИ.

Обратными тригонометрическими функциями являются arcsin, arccos, arctg и arcctg. Их необходимо использовать в том случае, когда нужно найти угол по заданному значению. Для этих целей применяются таблицы Брадиса, тригонометрический калькулятор и программное обеспечение, а также круг синусов и косинусов.

Последовательность действий: пошаговая инструкция по поиску тангенса от косинуса

Шаг 1: Возьмите значение косинуса, для которого нужно найти тангенс.

Шаг 2: Используя определение косинуса и теорему Пифагора, найдите значение синуса. Синус может быть вычислен как квадратный корень из (1 — косинус в квадрате).

Шаг 3: Поделите значение синуса на значение косинуса. Это даст вам значение тангенса.

Пример: Пусть у вас есть значение косинуса 0,5. Вычислим тангенс для этого значения.

Согласно шагу 2, найдем значение синуса:

синус = √(1 — косинус^2) = √(1 — 0,5^2) = √(1 — 0,25) = √0,75 = 0,866

Согласно шагу 3, найдем значение тангенса:

тангенс = синус / косинус = 0,866 / 0,5 = 1,732

Таким образом, для значения косинуса 0,5, тангенс будет равен 1,732.

Расчет тангенса и котангенса в компьютерных программах

Тангенс и котангенс: что это такое?

Тангенс и котангенс — это тригонометрические функции, которые используются для нахождения соотношений между двумя сторонами прямоугольного треугольника.
Тангенс определяется как отношение противоположного катета к прилежащему, а котангенс как отношение прилежащего катета к противоположному.

В компьютерных программах расчет тангенса и котангенса выполняется с помощью математических функций. Обычно это функции «tan» и «cot». Например, если нужно найти тангенс угла в радианах, можно использовать следующий код: tan(x), где «x» — значение угла в радианах.

Зачем нужны тангенс и котангенс в компьютерных программах?

Тангенс и котангенс могут использоваться во многих приложениях, где необходимо вычислить углы или расстояния между объектами. Например, в компьютерной графике тангенс используется для определения наклона линий и кривых. В астрономии тангенс используется для нахождения высоты объектов на небосводе. Котангенс же применяется для определения угла наклона плоскости.

Также тангенс и котангенс могут использоваться в физике, инженерных расчетах и других научных приложениях

Важно понимать, что правильный расчет тангенса и котангенса может существенно влиять на точность результатов, поэтому необходимо использовать соответствующие математические функции и учитывать единицы измерения

Тангенс и котангенс нужны для решения задач, где требуется найти угол между двумя линиями или найти расстояние между двумя точками. В геометрии тангенс и котангенс используются для вычисления высоты, основания, площади и объема различных геометрических фигур.

Тангенс и котангенс: каковы их различия и зачем нужны

В геометрии довольно часто приходится сталкиваться с задачами, для решения которых необходимо знание тангенса и котангенса. Эти две математические функции очень важны как для геометрических вычислений, так и для работы в ряде других областей науки и техники.

Тангенс и котангенс являются соответственно функциями тригонометрии синуса и косинуса, разделяющихся каждая своей обратной функцией. Тангенс и котангенс — это отношения двух катетов в прямоугольном треугольнике, примыкающих к углу α и называемого соответственно катетом противоположным и катетом прилежащим.

Тангенс и котангенс находят применение в вычислениях астрономических координат, математической статистике, вероятности, физике, инженерии и многих других областях. Например, в радиотехнике тангенс и котангенс используются для вычисления импеданса и проводимости сигналов. В машиностроении они используются для нахождения углов наклона поверхностей и степени прессовки сжатых материалов.

Тангенс – это отношение стороны прямоугольного треугольника, противоположной заданному углу, к прилежащей стороне. Применение тангенса может быть очень разнообразным, он используется для решения уравнений, нахождения длины сторон треугольника, векторов, скорости и т. д.

Практическое применение тангенса и котангенса в физике и инженерии

Также котангенс применяется в оптике при расчетах нахождения фокусных расстояний линз.

06.06.2019 19:36:58

2019-06-06 19:36:58

Любые данныеЛюбые данныеЛюбые данные Любые данные

Определение знака

Достоверность результата зависит от правильного решения. Неверный знак функции способен кардинально его изменить. Для безошибочного определения значений потребуются еще кое-какие знания. К ним относятся следующие: понятие о системе координат и теорема Пифагора, а также умение чертить окружность с определенным радиусом.

Системы координат, которые применяются при решении задач бывают полярными и декартовыми. Последние используются чаще, чем первые. Полярные применяются для решения задач из области высшей математики, а также в других сложных дисциплинах с физико-математическим уклоном.

Дополнительные сведения

Для определения знака применяется обыкновенная система координат с двумя осями. Одна из них (ОХ) является осью абсцисс, а другая (ОУ) — ординат. Ее центром, который совпадает с центром тригонометрической окружности, является точка «О». Очень часто для работы необходимо знание теоремы Пифагора. Ее формулировка имеет следующий вид: в любом прямоугольном треугольнике выполняется равенство квадрата гипотенузы и суммы квадратов катетов. Вторая формулировка записывается в виде формулы: с^2 = a^2 + b^2 (c, a и b — гипотенуза и два катета соответственно).

Необходимо обратить внимание на следующий факт: сумма всех углов треугольника составляет 180 градусов, то есть является развернутым углом. Математически утверждение можно записать следующим образом через углы а, b и c: а + b + c = 180

Кроме того, существуют и другие соотношения между острыми углами прямоугольного треугольника: cos (a) = sin (b), cos (b) = sin (a), tg (a) = ctg (b), и tg (b) = ctg (a).

Чтобы найти знаки тангенса и котангенса по четвертям, используются такие соотношения: tg (a) = sin (a) / cos (a) и ctg (a) = cos (a) / sin (a).

Построение окружности

Сделать «инструмент», который значительно ускорит процесс решения задач довольно просто. Для этого нужно построить декартовую систему координат и единичную окружность с центром в точке О (точка пересечения осей абсцисс и ординат). Горизонтальная ось обозначается «х», а вертикальная — «у».

Рекомендуется чертить произвольную окружность. Чертеж должен быть простым и понятным. Это называется масштабирование, при котором изображение не соответствует действительному размеру объекта. Его примером является обыкновенная географическая карта. Кроме того, при проектировании очень мелких деталей применяются чертежи, которые в несколько десятков или сотен раз превышают натуральные размеры. Обозначение точки на плоскости выполняется следующим образом:

Координаты заключаются в круглые скобки и разделяются «;».
На первом месте стоит значение, соответствующее оси абсцисс, а на втором — ординат: (x;y).

Окружность пересекает оси в четырех точках: (1;0), (0;1), (-1;0) и (0;-1). Четвертями называются области, которые делят систему координат на четыре равные части. Отсчет выполняется от первой четверти (x>0 и y>0) против часовой стрелки:

Значения по x и y больше 0 соответствуют первой четверти (I).
II: x<0 и y>0.
III: x<0 и y<0.
IV: x>0 и y<0.

Ось ординат соответствует всем значениям sin углов альфа и бета, а абсцисс — всем cos. Следовательно, по тригонометрической окружности можно определить знаки косинуса и синуса по четвертям. Рекомендуется отметить для удобства значения углов в радианах рядом с точками пересечения следующим образом:

0 и 2ПИ (0 и 360 градусов) — (1;0).
ПИ/2 (90) — (0;1).
3ПИ/2 (270) — (1;0).

Использование готового инструмента

Однако необязательно самостоятельно чертить единичную окружность для определения знаков. Можно воспользоваться уже готовыми вариантами (например, рис. 1).

Рисунок 1. Пример тригонометрического круга.

Косинус положителен в четвертях I и IV. Существуют области, где синус положителен: I и II. Функции tg и ctg положительны только в I и III четвертях. Однако перед тем, как приступить к решению задач, нужно понять термин «четность и нечетность функции». В тригонометрии они обладают такими свойствами:

cos(-a) = cos(a).
sin(-a) = -sin(a).
tg(-a) = -tg(a).
ctg(-a) = -ctg(a).

С помощью единичной окружности можно не только находить знаки функций, но и их значения. Например, для определения знака и значения cos(270) следует воспользоваться таким алгоритмом:

Определить четверть, в которой находится угол: 240 = 4ПИ/3 соответствует III четверти.
В III четверти величина функции принимает только отрицательные значения. Значит, перед ней следует поставить знак «минус».
Вычислить: cos(4ПИ/3) = — 1/2.

Когда угол представлен отрицательным значением, то следует правильно раскрыть скобки. Например, sin(-4ПИ/3) = — (-1/2) = 1/2.

Цикличность тангенса и его роль в тригонометрических уравнениях

Тангенс является одной из шести тригонометрических функций, которая определена для всех действительных чисел, кроме значений, при которых косинус равен нулю. Тангенс описывает соотношение между длинами противолежащего и прилежащего катета в прямоугольном треугольнике и может быть выражен через синус и косинус.

Особенностью тангенса является его периодичность. Тангенс имеет период 180 градусов или π радиан. Это означает, что значения тангенса повторяются с фиксированной частотой при увеличении аргумента на 180 градусов или π радиан. Таким образом, при решении тригонометрических уравнений, содержащих тангенс, мы можем использовать эту периодичность для нахождения всех возможных значений угла, удовлетворяющих уравнению.

При решении тригонометрических уравнений с тангенсом нам также могут пригодиться его основные свойства. Например:

Тангенс положителен в первой и третьей четвертях, а отрицателен во второй и четвертой четвертях.
Тангенс не имеет значений при аргументах, при которых косинус равен нулю (то есть при углах, кратных 90 градусам или π/2 радиан). В этих точках тангенс имеет вертикальные асимптоты.
Тангенс является неограниченной функцией. Он стремится к положительной или отрицательной бесконечности при приближении аргумента к значениям, при которых косинус равен нулю.

Важно помнить, что при решении тригонометрических уравнений с тангенсом мы должны учитывать и периодичность функции, и ее особенности, чтобы получить все корни уравнения и действительные значения угла

Свойства синуса, косинуса, тангенса и котангенса

В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.

Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .

Знаки тригонометрических функций по четвертям

Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 ( 1 , 0 ) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 ( x , y ) . В зависимости от того, в какой четверти будет лежать точка A 1 ( x , y ) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.

Для наглядности приведем иллюстрацию.

Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.

При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.

Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 ( x , y ) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.

Косинус — это абсцисса точки A 1 ( x , y ) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.

Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.

Свойство периодичности

Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.

При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.

Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.

Математически данное свойство записывается так:

sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α

Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.

sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5

t g ( — 689 ° ) = t g ( 31 ° + 360 ° · ( — 2 ) ) = t g 31 ° t g ( — 689 ° ) = t g ( — 329 ° + 360 ° · ( — 1 ) ) = t g ( — 329 ° )

Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов

Вновь обратимся к единичной окружности.

Точка A 1 ( x , y ) — результат поворота начальной точки A 0 ( 1 , 0 ) вокруг центра окружности на угол α . Точка A 2 ( x , — y ) — результат поворота начальной точки на угол — α .

Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты ( x , y ) , а вторая — ( x , — y ) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:

sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y

Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.

Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов

sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α

Согласно этому свойству, справедливы равенства

sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °

Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.

Таблица тангенсов

х (°)» порядок данных=»x (°)«стиль = «минимальная ширина: 34,7656%»; ширина:34,7656%;»>x (°)	х (строка)» порядок данных=»x (рад)«стиль = «минимальная ширина: 33,5938%; ширина:33,5938%;»>x (строка)	х»заказ данных=»tg x«стиль = «минимальная ширина: 31,6406%»; ширина:31,6406%;»>тг х
-90°	-π/2	-∞
-71,565°	-1,2490	-3
-63,435°	-1,1071	-2
-60°	-π/3	3″ порядок данных=»-√3″>-√3
-45°	-π/4	-1
-30°	-π/6	3″ порядок данных=»-1/√3″>-1/√3
-26,565°	-0,4636	-0,5
0°
26,565°	0,4636	0,5
30°	π/6	3″ порядок данных=»1/√3″>1/√3
45°	π/4	1
60°	π/3	3″заказ данных=»√3″>√3
63,435°	1.1071	2
71,565°	1.2490	3
90°	π/2	∞

Углы с отрицательным синусом

Синус угла определяется соотношением между противолежащим катетом и гипотенузой прямоугольного треугольника. Обычно синус принимает положительные значения, но существуют углы, при которых синус отрицательный.

Углы с отрицательным синусом находятся во втором и третьем квадрантах геометрической системы координат. В этих квадрантах противолежащий катет прямоугольного треугольника отрицателен, а гипотенуза положительна.

Понимание углов с отрицательным синусом важно при решении задач, связанных с геометрией, тригонометрией и физикой. Например, векторы с отрицательным синусом могут указывать направления с противоположными значениями наклона, а это важно при изучении движения тел в пространстве

Пример:

Если угол А лежит во втором квадранте и синус этого угла равен -0,5, то мы знаем, что противолежащий катет имеет отрицательную длину, а гипотенуза положительна. Это может быть полезной информацией при дальнейшем анализе и вычислениях.