Определение всех геометрических фигур их свойства и формулу площади

Введение

«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия».

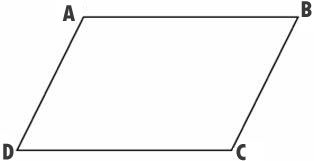
Свойство противолежащих сторон параллелограмма

У параллелограмма противолежащие стороны равны.

Доказательство.

Пусть ABCD – данный параллелограмм. И пусть его диагонали пересекаются в точке O.Так как Δ AOB = Δ COD по первому признаку равенства треугольников (∠ AOB = ∠ COD, как вертикальные, AO=OC, DO=OB, по свойству диагоналей параллелограмма), то AB=CD. Точно также из равенства треугольников ВОС и DOA, следует что BC=DA. Теорема доказана.

Свойство противолежащих углов параллелограмма

У параллелограмма противолежащие углы равны.

Доказательство.Пусть ABCD – данный параллелограмм . И пусть его диагонали пересекаются в точке O.Из доказанного в теореме о свойства противолежащих сторон параллелограмма Δ ABC = Δ CDA по трем сторонам (AB=CD, BC=DA из доказанного, AC – общая). Из равенства треугольников следует, что ∠ ABC = ∠ CDA.Так же доказывается, что ∠ DAB = ∠ BCD, которое следует из ∠ ABD = ∠ CDB. Теорема доказана.

Свойство диагоналей параллелограмма

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Доказательство.

Пусть ABCD – данный параллелограмм. Проведем диагональ AC. Отметим на ней середину O. На продолжении отрезка DO отложим отрезок OB 1 , равный DO.По предыдущей теореме AB 1 CD – параллелограмм. Поэтому, прямая AB 1 параллельна DC. Но через точку A можно провести только одну прямую, параллельную DC. Значит, прямая AB 1 совпадает с прямой AB.Также доказывается, что BC 1 совпадает с BC. Значит, точка С совпадает с С 1 . параллелограмм ABCD совпадает с параллелограммом AB 1 CD. Следовательно, диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Теорема доказана.

В учебниках для обычных школ (например, в Погорелове) доказывается она так: диагонали делят параллелограмм на 4 треугольника. Рассмотрим одну пару и выясним — они равны: основания у них — противоположные стороны, прилежащие к нему соответствующие углы равны как вертикальные при параллельных прямых. То есть отрезки диагоналей попарно равны. Всё.

Всё ли?Выше доказано, что точка пересечения делит диагонали пополам — если существует. Само её существование приведённое рассуждение не доказывает ни в коей мере. То есть часть теоремы «диагонали параллелограмма пересекаются» остаётся недоказанной.

Забавно, что доказать эту часть намного сложнее. Следует это, кстати, из более общего результата: у любого выпуклого четырёхугольника диагонали будут пересекаться, у любого невыпуклого — не будут.

О равенстве треугольников по стороне и двум прилежащим к ней углам (второй признак равенства треугольников) и другие.

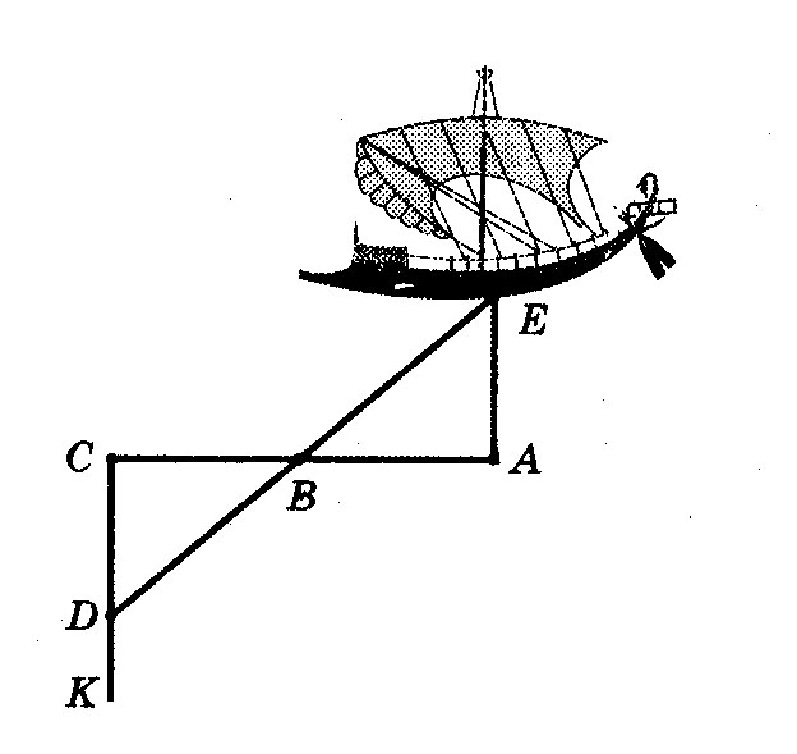
Теореме о равенстве двух треугольников по стороне и двум прилежащим к ней углам Фалес нашел важное практическое применение. В гавани Милета был построен дальномер, определяющий расстояние до корабля в море

Он представлял собой три вбитых колышка А, В и С (АВ = ВС) и размеченную прямую СК, перпендикулярную.СА. При появлении корабля на прямой СК находили точку D такую, чтобы точки D, .В и Е оказывались на одной прямой. Как ясно из чертежа, расстояние CD на земле является искомым расстоянием до корабля.

Диагонали квадрата точкой пересечения делятся пополам?
Диагонали параллелограмма равны?
Противолежащие углы параллелограмма равны?
Сформулируйте определение параллелограмма?
Сколько признаков параллелограмма?
Может ли ромб быть параллелограмом?

Диагонали делятся пополам

Так как параллелограмм — это выпуклый четырехугольник, то у него две две диагонали, и они пересекаются. Пусть дан параллелограмм ABCD, его диагонали AC и BD пересекаются в точке E. Рассмотрим образованные ими треугольники ABE и CDE.

У этих треугольников стороны AB и CD равны как противоположные стороны параллелограмма. Угол ABE равен углу CDE как накрест лежащие при параллельных прямых AB и CD. По этой же причине ∠BAE = ∠DCE. Значит, ∆ABE = ∆CDE по двум углам и стороне между ними.

Также можно заметить, что углы AEB и CED вертикальные, а следовательно, тоже равны друг другу.

Так как треугольники ABE и CDE равны друг другу, то равны и все их соответствующие элементы. Стороне AE первого треугольника соответствует сторона CE второго, значит, AE = CE. Аналогично BE = DE. Каждая пара равных отрезков составляет диагональ параллелограмма. Таким образом доказано, что диагонали параллелограмма делятся точкой пересечения пополам
.

Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны, т. е. лежат на параллельных прямых
(рис.1).

Теорема 1.
О свойстве сторон и углов параллелограмма.
В параллелограмме противоположные стороны равны, противоположные углы равны и сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.

Доказательство. В данном параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC (рис.2).

Эти треугольники равны, так как ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (накрест лежащие углы при параллельных прямых), а сторона АС общая. Из равенства Δ ABC = Δ ADC следует, что АВ = CD, ВС = AD, ∠ B = ∠ D. Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых. Теорема доказана.

Замечание. Равенство противоположных сторон параллелограмма означает, что отрезки параллельных, отсекаемых параллельными, равны.

Следствие 1. Если две прямые параллельны, то все точки одной прямой находятся на одном и том же расстоянии от другой прямой.

Доказательство. В самом деле, пусть а || b (рис.3).

Проведем из каких-нибудь двух точек В и С прямой b перпендикуляры ВА и CD к прямой а. Так как АВ || CD, то фигура ABCD — параллелограмм, и следовательно, АВ = CD.

Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из прямых до другой прямой.

По доказанному оно равно длине перпендикуляра, проведенного из какой-нибудь точки одной из параллельных прямых к другой прямой.

Пример 1.
Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.

Решение.

По теореме 1 противоположные стороны параллелограмма равны. Обозначим одну сторону параллелограмма через х, другую через у. Тогда по условию
$$\left\{\begin{matrix}
2x + 2y = 122
\\x — y = 25
\end{matrix}\right.$$
Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.

Пример 2.

Решение.

Пусть условию задачи отвечает рисунок 4.

Обозначим АВ через х, а ВС через у. По условию периметр параллелограмма равен 10 см, т. е. 2(x + у) = 10, или х + у = 5.
Периметр треугольника ABD равен 8 см. А так как АВ + AD = х + у = 5 то BD = 8 — 5 = 3 .
Итак, BD = 3 см.

Пример 3.
Найти углы параллелограмма, зная, что один из них больше другого на 50°.

Решение.

Пусть условию задачи отвечает рисунок 5.

Обозначим градусную меру угла А через х. Тогда градусная мера угла D равна х + 50°.

Углы BAD и ADC внутренние односторонние при параллельных прямых АВ и DC и секущей AD. Тогда сумма этих названных углов составит 180°, т. е.

х + х + 50° = 180°, или х = 65°. Таким образом, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.

Пример 4.
Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?

Решение.

Пусть условию задачи отвечает рисунок 6.

АЕ — биссектриса острого угла параллелограмма. Следовательно, ∠ 1 = ∠ 2.

В этом разделе мы рассматриваем геометрический объект параллелограмм. Все элементы параллелограмма наследуются от четырехугольника, поэтому рассматривать их мы не будем. А вот свойства и признаки заслуживают детального рассмотрения. Мы разберем:

чем признак отличается от свойства;
рассмотрим основные свойства и признаки, которые изучают в программе 8 класса;
сформулируем еще два дополнительных свойства, которые получим при решении опорных задач.

Как отличить параллелограмм от прямоугольника и ромба по сторонам

1. Параллелограмм:

Все стороны параллелограмма имеют одинаковую длину и параллельны друг другу.
Углы между сторонами могут быть любыми, но противоположные углы равны.

2. Прямоугольник:

У прямоугольника все стороны также имеют одинаковую длину и параллельны друг другу.
Углы между сторонами равны по 90 градусов.

3. Ромб:

У ромба все стороны имеют одинаковую длину, как и у параллелограмма и прямоугольника.
Углы между сторонами ромба равны.
Два угла ромба равны 90 градусов, как и у прямоугольника.

Итак, вот как можно отличить параллелограмм от прямоугольника и ромба по сторонам. Если все стороны четырехугольника имеют одинаковую длину и параллельны друг другу, то это параллелограмм. Если углы между сторонами равны 90 градусов, то это прямоугольник. Если все углы и стороны четырехугольника равны, то это ромб.

Полезные советы для решения задач

Читайте условие задачи внимательно

Важно понимать, что именно требуется от вас в задании и какие данные есть

Рисуйте схемы и картинки. Наглядное представление поможет вам лучше понять задание и найти решение.

Используйте формулы и свойства. Заранее знание формул и свойств, связанных с темой задачи, может существенно облегчить ее решение.

Решайте задачу поэтапно. Разбейте задачу на несколько частей и решите каждую отдельно. Это поможет вам не упустить важные детали и избежать ошибок.

Проверяйте результат. После завершения решения задачи не забывайте его проверить. При ошибке вернитесь к предыдущим этапам и уточните решение.

Не бойтесь задавать вопросы. Если вы не уверены в своем решении или не понимаете условие задачи — не стесняйтесь обратиться к учителю, он поможет вам разобраться в теме.

Практикуйтесь. Чем больше задач вы решите, тем больше опыта вы наберетесь. Не забывайте тренироваться и улучшать свои навыки.

Важно:
Не списывайте решения. Это не поможет вам научиться решать задачи и может привести к неприятностям

В заключение, помните, что решение математических задач требует терпения, внимательности и усидчивости.

Теорема о параллелограмме

Теорема: параллелограммы на одном основании и между одинаковыми параллелями имеют одинаковую площадь.

Доказательство: Предположим, что есть два параллелограмма ABCD и ABEF с одним и тем же основанием DC и между одинаковыми параллельными прямыми AB и FC.

Доказать: площадь параллелограмма ABCD = площадь параллелограмма ABEF.

На приведенном ниже рисунке два параллелограмма ABCD и ABEF лежат между одними и теми же параллельными прямыми и имеют одно и то же основание. Площадь ABDE является общей для обоих параллелограммов. Если присмотреться к двум треугольникам, △BCD и △AEF могут оказаться конгруэнтными.

BC = AE (противоположные стороны параллелограмма),

∠BCD = ∠AEF (это соответствующие углы, потому что BC || AE и CE являются секущими).

∠BDC = ∠AFE (это соответствующие углы, поскольку BD || AF и FD являются секущими).

Таким образом, по критерию ASA конгруэнтных треугольников. Эти два треугольника конгруэнтны, и они должны иметь равные площади.

площадь (BCD) = площадь (AEF)

⇒ площадь(BCD) + площадь(ABDE) = площадь(AEF) + площадь(ABDE)

⇒ площадь(ABCD) = площадь(ABEF)

Следовательно, параллелограммы, лежащие между одними и теми же параллельными прямыми и имеющие общее основание, имеют одинаковую площадь.

В каких областях и сферах применяются эти формы

Параллелограммы находят свое применение в различных областях. Например, в архитектуре они используются для создания фасадов зданий, формирования витражных окон или создания крыш. Также параллелограммы встречаются в дизайне интерьеров: они могут служить основой для расстановки мебели или создания художественных композиций.

Прямоугольники широко применяются в конструкции строений, таких как двери и окна. Они обеспечивают простоту и легкость в производстве, а также отличные свойства прочности и устойчивости. В дизайне, прямоугольники часто используются для создания рамок, плакатов или рекламных щитов.

Ромбы находят свое применение в различных сферах. В геометрическом моделировании они используются для создания трехмерных моделей, таких как украшения, кристаллические структуры или объемные фигуры. В технике, ромбы они могут служить основой для создания роликовых подшипников или крепежных элементов.

Таким образом, параллелограммы, прямоугольники и ромбы находят широкое применение в разных областях и сферах, благодаря своим уникальным свойствам и возможностям формирования.

Формулы для треугольников

Имеется несколько формул площади треугольника. Если в треугольнике известны две величины: во-первых, длина стороны, а во-вторых, высота, опущенная из противоположного угла перпендикулярно этой стороне, то площадь можно определить, умножив длину на высоту и разделив полученное произведение на два. Выглядит формула так: S = ½ * a * h. Буквой a обозначена длина, буквой h — высота.

При известности всех трёх сторон — a, b, c, широко применяется формула, названная в честь Герона — математика из Древней Греции: S = √(p*(p — a)*(p — b)*(p — c)). Величина p — это половина от периметра треугольника (полупериметр). Чтобы его рассчитать, необходимо суммировать все стороны и разделить сумму на два: (a + b + c)/2.

Для ещё одной формулы требуются следующие данные:

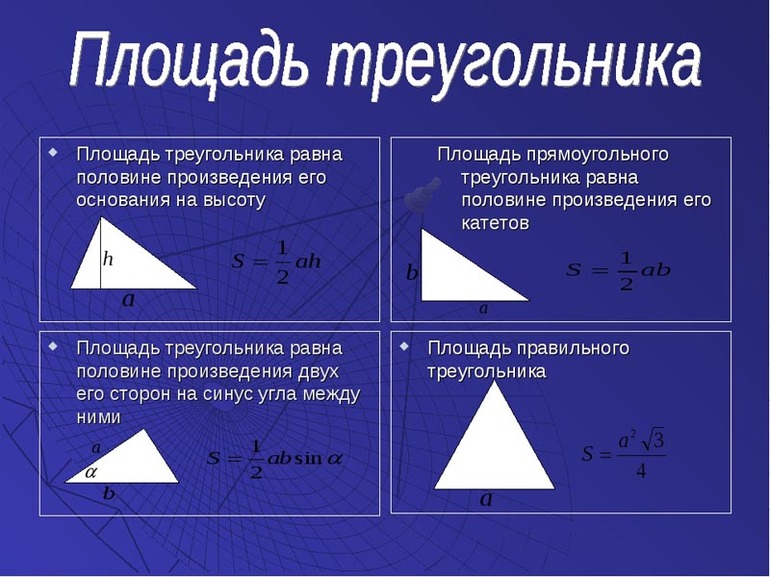
Тогда расчёт можно произвести таким способом: S = ½ * a * b * sin γ. Синус угла является одной из тригонометрических функций, представляющей собой результат деления (отношение) в прямоугольном треугольнике противолежащего (дальнего) катета к гипотенузе (сторона напротив прямого угла). Значение sin γ для конкретного угла можно посмотреть в специальной таблице.

Когда два треугольника являются подобными (подобие означает, что у них равны углы и стороны пропорциональны), то отношение их площадей соответствует отношению возведённых в квадрат сторон. Такое отношение сторон для них (например, AB: A (1) B (1)) именуется коэффициентом подобия (k). Поэтому отношение площадей равняется коэффициенту подобия в квадрате.

Если в треугольнике даны все стороны, тогда, кроме формулы Герона, есть возможность воспользоваться ещё одним способом. Он основан на том, что можно вписать любой треугольник в круг. Зная такую величину, радиус окружности и три стороны треугольника, производится расчёт: S = (a * b * c) / 4 R.

https://youtube.com/watch?v=aXyKgX6RAqw

Параллелограмм — выпуклый четырехугольник

Докажем сначала теорему о том, что параллелограмм является выпуклым четырехугольником
. Многоугольник является выпуклым тогда, когда какая бы его сторона не была продлена до прямой, все остальные стороны многоугольника окажутся по одну сторону от этой прямой.

Пусть дан параллелограмм ABCD, у которого AB противоположная сторона для CD, а BC — противоположная для AD. Тогда из определения параллелограмма следует, что AB || CD, BC || AD.

У параллельных отрезков нет общих точек, они не пересекаются. Это значит, что CD лежит по одну сторону от AB. Поскольку отрезок BC соединяет точку B отрезка AB с точкой C отрезка CD, а отрезок AD соединяет другие точки AB и CD, то отрезки BC и AD также лежат по ту же сторону от прямой AB, где лежит CD. Таким образом, все три стороны — CD, BC, AD — лежат по одну сторону от AB.

Аналогично доказывается, что по отношению к другим сторонам параллелограмма три остальные стороны лежат с одной стороны.

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Свойства параллелограмма в геометрии

1. Противоположные стороны параллельны

Все стороны параллелограмма имеют одинаковую длину, причем каждая сторона параллельна соответствующей ей противоположной стороне. Таким образом, любая предполагаемая линия, соединяющая противоположные вершины параллелограмма, будет параллельна боковым сторонам.

2. Противоположные углы равны

Все углы параллелограмма равны по мере, противоположные углы имеют равные величины. Например, углы, образованные противоположными сторонами параллелограмма, имеют равную меру. Это является следствием того, что противоположные стороны параллелограмма параллельны и одинаково ориентированы.

3. Диагонали пересекаются в своей середине

Диагонали параллелограмма делятся пополам в своей точке пересечения. Другими словами, точка пересечения диагоналей является серединой каждой из диагоналей. Это свойство часто используется для нахождения точки пересечения диагоналей или для вычисления длин диагоналей.

4. Параллелограмм имеет две оси симметрии

Параллелограмм имеет две оси симметрии. Одна ось симметрии проходит через середину стороны и соединяет противоположные вершины, а другая ось симметрии проходит через середину диагонали и соединяет противоположные углы. Это свойство подразумевает, что параллелограмм можно перевернуть вокруг оси симметрии так, чтобы он выглядел одинаково.

5. Периметр параллелограмма

Периметр параллелограмма вычисляется по формуле: P = 2(a + b), где a и b — длины сторон параллелограмма. Формула основана на том факте, что стороны параллельны и одинаково ориентированы.

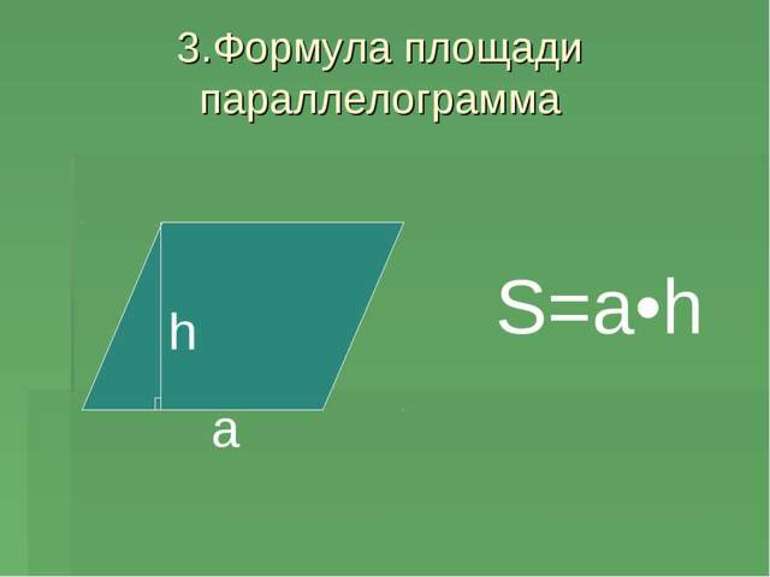
6. Площадь параллелограмма

Площадь параллелограмма вычисляется по формуле: S = a * h, где a — длина основания параллелограмма, h — высота параллелограмма, опущенная на это основание. Формула также основана на том факте, что стороны параллельны и одинаково ориентированы.

Равенство противоположных сторон и углов

Кроме того, у параллелограмма также равны противоположные углы. Это означает, что углы A и C параллелограмма равны между собой, а углы B и D также равны. Это свойство является следствием параллельности противоположных сторон.

Например, рассмотрим параллелограмм ABCD:

Сторона	Длина	Угол
AB	6 см	40°
BC	6 см	140°
CD	6 см	40°
DA	6 см	140°

В данном примере видно, что все стороны и углы параллелограмма ABCD равны. Это свидетельствует о равенстве противоположных сторон и углов в параллелограмме, что является одним из его основных свойств.

Сумма углов внутри параллелограмма равна 360 градусов

Чтобы убедиться в этом свойстве, рассмотрим поочередно каждый из углов параллелограмма:

1) Первый угол — угол A. Он противоположен углу C и равен ему по величине.

2) Второй угол — угол B. Он противоположен углу D и равен ему по величине.

3) Третий угол — угол C. Он противоположен углу A и равен ему по величине.

4) Четвертый угол — угол D. Он противоположен углу B и равен ему по величине.

Таким образом, сумма углов A, B, C и D внутри параллелограмма равна 360 градусов.

Важно отметить, что данное свойство относится только к параллелограммам и не выполняется для других четырехугольников. Поэтому, если известна сумма углов внутри некого четырехугольника, это еще не гарантирует, что он является параллелограммом

Свойства четырехугольников. Параллелограмм

Свойства параллелограмма

Внимание! Слова «свойства параллелограмма
» означают, что если у тебя в задаче есть
параллелограмм, то всем нижеследующим можно пользоваться

Теорема о свойствах параллелограмма.

В любом параллелограмме:

Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ
теорему.

Итак, почему верно 1)?

Раз — параллелограмм, то:

как накрест лежащие
как накрест лежащие.

Значит, (по II признаку: и — общая.)

Ну вот, а раз, то и — всё! — доказали.

Но кстати! Мы ещё доказали при этом и 2)!

Почему? Но ведь (смотри на картинку), то есть, а именно потому, что.

Осталось только 3).

Для этого всё-таки придётся провести вторую диагональ.

И теперь видим, что — по II признаку (угла и сторона «между» ними).

Свойства доказали! Перейдём к признакам.

Признаки параллелограмма

Напомним, что признак параллелограмма отвечает на вопрос «как узнать?», что фигура является параллелограммом.

В значках это так:

Почему? Хорошо бы понять, почему — этого хватит. Но смотри:

Ну вот и разобрались, почему признак 1 верен.

Ну, это ещё легче! Снова проведём диагональ.

А значит:

И
тоже несложно. Но …по-другому!

Значит, . Ух! Но и — внутренние односторонние при секущей!

Поэтому тот факт, что означает, что.

А если посмотришь с другой стороны, то и — внутренние односторонние при секущей! И поэтому.

Видишь, как здорово?!

И опять просто:

Точно так же, и.

Обрати внимание:
если ты нашел хотя бы
один признак параллелограмма в своей задаче, то у тебя точно
параллелограмм, и ты можешь пользоваться всеми
свойствами параллелограмма. Для полной ясности посмотри на схему:

Для полной ясности посмотри на схему:

Площадь четырёхугольников

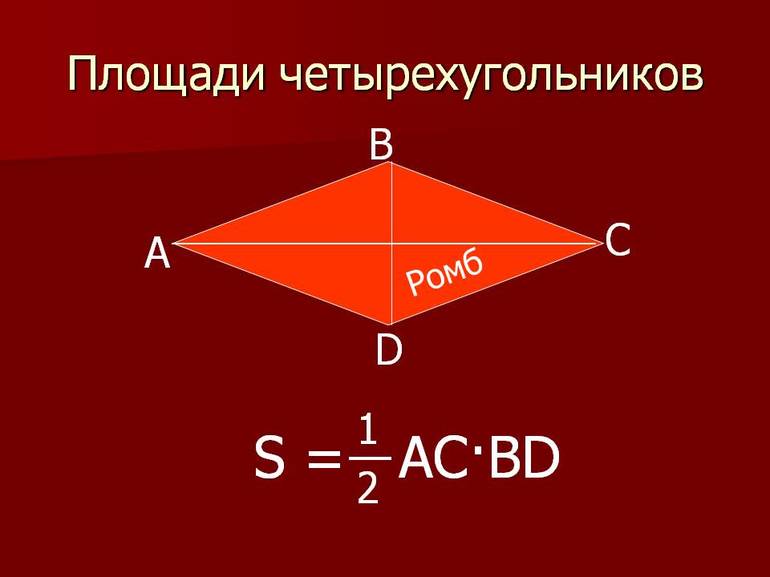
Четырёхугольник — это одна из фигур в геометрии (многоугольник), имеющая четыре стороны, а также четыре вершины, три из которых не находятся на одной прямой. Четырёхугольник называется выпуклым, если он располагается по одну сторону относительно прямой, являющейся продолжением любой из его сторон.

К выпуклым четырёхугольникам относятся практически все известные фигуры, имеющие четыре вершины, а также четыре стороны. Основными их видами выступают: 1) ромб; 2) прямоугольник; 3) трапеция; 4) квадрат; 5) параллелограмм.

Квадрат и прямоугольник

Самый простой способ вычисления площади квадрата — умножить сторону «саму на себя», иными словами, возвести в квадрат длину любой из его сторон (S = a 2 ). Такой расчёт обусловлен особым признаком квадрата — тем, что все его стороны являются абсолютно равными между собой, поэтому квадрат называется правильной фигурой.

Параллелограмм, ромб и трапеция

Параллелограмм представляет собой четырёхугольник, в котором имеются два противоположных друг другу тупых угла и два — острых.

Применяются три формулы площади параллелограмма:

Ромб похож на параллелограмм с одним отличием: он является равносторонним. Поэтому для вычисления площади ромба используются похожие формулы:

Трапеция является геометрической фигурой, имеющей такие элементы: два параллельных основания — верхнее и нижнее, две боковые стороны, расположенные к нижнему основанию под острым углом. Что касается боковых сторон, то они могут быть как равными по длине (так называемая равнобедренная трапеция), так и разными.

В связи с тем, что в «составе» трапеции можно «выделить» прямоугольник и два расположенных по бокам от него треугольника, то можно определить площадь по специальной формуле Герона: S = (a + b): | a + b | * √(p — a) * (p — b) * (p — a — c) * (p — a — d).

В этой формуле имеются следующие обозначения:

Выпуклый четырёхугольник

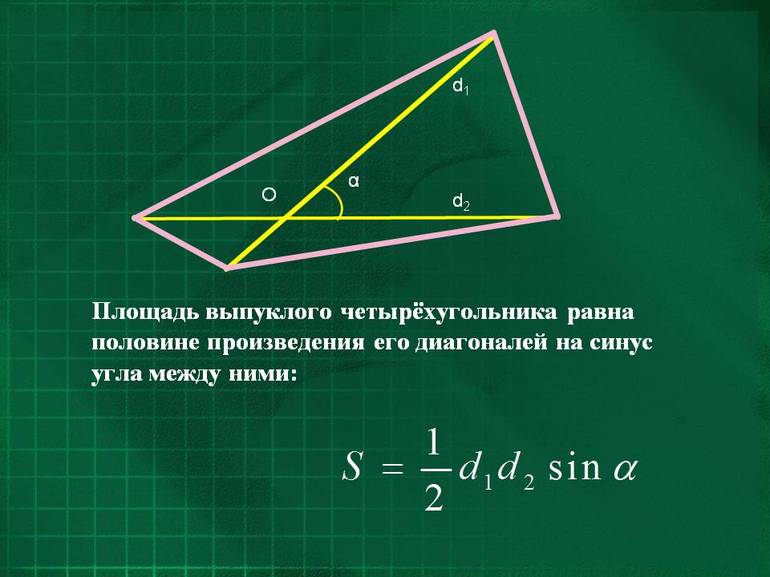
В отношении всех иных выпуклых четырёхугольников, то есть имеющих разные по длине стороны и разные углы, разработаны свои формулы вычисления площади.

Прежде всего, можно перемножить две диагонали, а также синус образуемого ими угла, разделив общий результат на два, то есть применить формулу: S = ½ d (1) * d (2) * sin γ.

В том случае, когда внутри выпуклого четырёхугольника, так же как и внутри треугольника, может быть вписан круг, то для нахождения площади четырёхугольной фигуры, требуется определить две величины:

Для тех случаев, когда круг может быть очерчен вокруг четырёхугольника, применяется другая формула. Для её использования все стороны фигуры должны быть известны. Они обозначаются буквами a, b, c, d. Рассчитывается половина периметра: p = (a + b + c + d)/2. Затем определяется площадь: S = √(p — a)(p — b)(p — c)(p — d).

Когда конфигурация четырёхугольника такова, что не позволяет возле него описать круг, то в связи с этим формула площади немного дополняется: S = √(p — a)(p — b)(p — c)(p — d) — abcd cos 2 γ.

Коэффициент γ представляет собой половину от суммы двух противоположных углов четырёхугольной фигуры: γ = (угол (1) + угол (2)) / 2.

Определение и свойства квадрата

Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.

Четырёхугольник называют квадратом в следующих случаях:

Если это прямоугольник, у которого длина a и ширина b равны.
Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.

К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:

Диагонали перпендикулярны относительно друг друга (свойство ромба).
Точка пересечения совпадает с центром вписанной окружности.
Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.

Приведём часто используемые формулы для вычисления периметра, площади и элементов квадрата:

Диагональ d = a √2.
Периметр P = 4 a.
Площадь S = a ².
Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.

Как построить прямоугольник и параллелограмм

Прямоугольник и параллелограмм — это четырехугольники, которые имеют определенные свойства и пересекаются с другими фигурами под определенным углом. Для построения этих фигур существует несколько способов:

Построение прямоугольника

1. На листе бумаги проведите две перпендикулярные линии, представляющие собой стороны будущего прямоугольника.

2. Установите точки пересечения линий в качестве вершин прямоугольника.

3. Откладывайте от каждой вершины по одинаковой длине вдоль каждой линии, чтобы получить стороны прямоугольника.

4. Соедините полученные точки линиями и вы получите прямоугольник.

Построение параллелограмма

1. На листе бумаги проведите отрезок, который будет являться одной из сторон будущего параллелограмма.

3. Продлите полученные отрезки так, чтобы они пересеклись и образовали четырехугольник с двумя параллельными сторонами.

4. Убедитесь, что две параллельные стороны имеют одинаковую длину, чтобы получить правильный параллелограмм.

Здесь важно помнить о том, что стороны параллелограмма должны быть параллельными, а углы на противоположных сторонах должны быть равными. Для построения фигур используйте линейку и угольник для получения точных значений

Свойства четырехугольников. Прямоугольник.

Свойства прямоугольника:

Пункт 1) совсем очевидный — ведь просто выполнен признак 3 ()

А пункт 2) — очень важный
. Итак, докажем, что

А значит, по двум катетам (и — общий).

Ну вот, раз треугольники и равны, то у них и гипотенузы и тоже равны.

Доказали, что!

И представь себе, равенство диагоналей — отличительное свойство именно прямоугольника среди всех параллелограммов. То есть верно такое утверждение^

Давай поймём, почему?

Значит, (имеются в виду углы параллелограмма). Но ещё раз вспомним, что — параллелограмм, и поэтому.

Значит, . Ну и, конечно, из этого следует, что каждый из них по! Ведь в сумме-то они должны давать!

Вот и доказали, что если у параллелограмма
вдруг (!) окажутся равные диагонали, то это точно прямоугольник
.

Но! Обрати внимание!
Речь идёт о параллелограммах
! Не любой
четырехугольник с равными диагоналями — прямоугольник, а только
параллелограмм!

2.3 Опорная задача №4 (Свойство угла между высотами параллелограмма)

Дано:
ABCD

— параллелограмм, BK

и BM

— его высоты, $\angle KBM = 60^0$
.

Найти:
$\angle ABK$, $\angle A$

Решение:

Приступая к решению этой задачи, нужно иметь ввиду следующее:

высота в параллелограмме перпендикулярна обеим противоположным сторонам

Например, если отрезок $BM$ проведен к стороне $DC$ и является его высотой ($BM \perp DC$), то этот же отрезок будет высотой к противположной стороне ($BM \perp BA$). Это следует из параллельности сторон $AB \parallel DC$.

При решении этой задачи, ценным является свойство, которое мы получаем.

Дополнительное свойство.
Угол между высотами параллелограмма, проведенными из его вершины, равен углу при соседней вершине.

Частные случаи параллелограммов

Как мы знаем, по определению, чтобы быть параллелограммом, многоугольник должен иметь параллельные стороны. Есть три четырехугольника, которые рассматриваются как частные случаи параллелограмма: прямоугольник, ромб и квадрат.

Квадратный

мы называем квадратный четырехсторонний многоугольник с четырьмя сторонами и четырьмя равными углами — каждый угол равен точно 90 градусам. Поскольку квадрат является параллелограммом, все свойства действительны для квадрата.

Площадь квадрата и его периметр рассчитываются аналогично тому, как это делается с параллелограммом, но поскольку все стороны квадрата равны, мы можем представить площадь и периметр квадрата следующим образом:

A = l²

P = 4,1

Прямоугольник

О прямоугольник это параллелограмм, у которого есть все совпадающие углы. Он получил такое название, потому что все твои углы прямые, то есть четыре угла составляют 90º. Область прямоугольника идентична области параллелограмма, но мы можем рассматривать вертикальную сторону как высоту, в конце концов, она перпендикулярна основанию.

А =а.б

P = 2 (а + б)

Алмаз

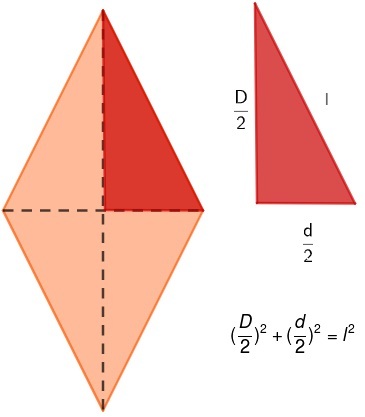
О алмаз это параллелограмм, у которого все стороны равны. Учтите, что ограничений по углам нет, они могут быть разными или нет. В отличие от предыдущих примеров, Расчет площади алмаза производится по его диагоналям. Также существует очень важная взаимосвязь между диагоналями алмаза и его стороной.

D: большая диагональ

d: малая диагональ

l: сторона

Для любого ромба мы знаем, что диагонали пересекаются в средней точке, образуя четыре прямоугольных треугольника. Анализируя один из этих треугольников, можно увидеть Пифагорейские отношения между стороной и половиной каждой из диагоналей.

Также доступ: длина окружности и площадь круга

Простейшие виды фигур

Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.

Точка

Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик

Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом

Например, A, B, C или 1, 2, 3.

Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.

Самыми простейшими фигурами являются луч и отрезок.

Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.
Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.

Линия

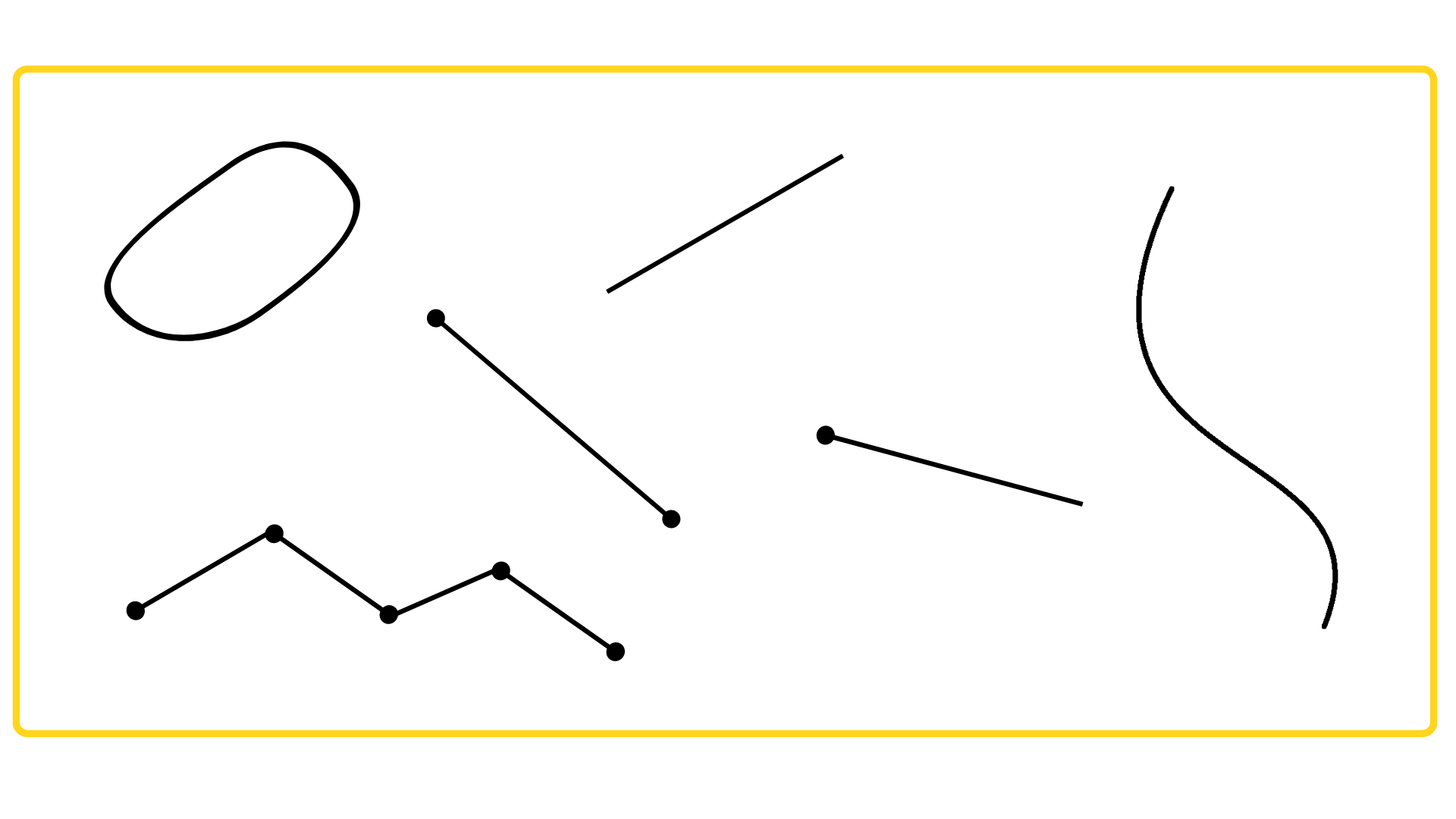
Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными.

Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
Разомкнутая — когда начало и окончание линии не соединены.
Прямая — непрерывная линия без изменений.
Кривая — отличная от прямой линии.
Ломаная — когда соединены отрезки не под углом 180 градусов.

Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.