Существует ли треугольник, у которого все стороны невырождены и отличаются друг от друга в целых числах

Треугольник с двумя углами в 90 градусов

Такой треугольник называется «прямоугольным» и является основой для изучения тригонометрии. Два катета, пересекающиеся под прямым углом, обозначаются a и b, а гипотенуза — c. Известно, что гипотенуза всегда больше любого из катетов и можно вычислить ее длину по формуле:

c = √(a² + b²)

Прямоугольный треугольник встречается во многих областях, например, в геометрии, физике и инженерии. Он используется при расчете траектории движения тела, переноса картинок на экране компьютера и даже в космических экспедициях для ориентации в космосе.

• Примеры применения прямоугольного треугольника:
• Расчет длины кабеля, необходимого для соединения двух точек на разной высоте
• Расчет расстояния до недоступных объектов с помощью лазерного измерителя
• Расчет траектории падения парашютиста для безопасного приземления

Прямоугольный треугольник — важный элемент в повседневной жизни и науке. Его знание позволяет решать широкий круг задач, связанных с расчетами и конструированием. Основные теоремы, связанные с прямоугольным треугольником, были известны еще Древней Греции и с тех пор активно применяются в науке и технике.

Треугольник — формулы, свойства, элементы и примеры с решением

Треугольники и его элементы:

Определение: Треугольником называется геометрическая фигура, которая состоит из трех точек (вершин треугольника), не лежащих на одной прямой, и трех отрезков (сторон треугольника), попарно соединяющих эти точки.

Треугольник обозначается знаком

На рисунке 54 изображен треугольник с вершинами А, B, С и сторонами АВ, ВС, АС. Этот треугольник можно обозначить так:

Определение: Углом треугольника ABC при вершине А называется угол ВАС.

Угол треугольника обозначают тремя буквами (например, «угол ABC») или одной буквой, которая указывает его вершину (например, «угол А треугольника ABC »).

Если вершина данного угла треугольника не принадлежит стороне, то говорят, что данный угол противолежащий этой стороне. В противном случае угол является прилежащим к стороне. Так, в треугольнике ABC угол А — прилежащий к сторонам АВ и АС и противолежащий стороне ВС. Стороны и углы треугольника часто называют его элементами

Определение: Периметром треугольника называется сумма всех его сторон.

Периметр — от греческого «пери» — вокруг и «метрео» — измеряю, измеренный вокруг.

Периметр обозначается буквой Р. По определению —

Роль треугольника в геометрии трудно переоценить. Ученые не зря называют треугольники клетками организма геометрии. Действительно, многие более сложные геометрические фигуры можно разбить на треугольники.

В этой главе мы не только изучим «внутрен нее устройство» треугольников и выделим их виды, но и докажем признаки, по которым можно установить равенство треугольников, сравнивая их стороны и углы. Полученные в ходе наших рассуждений теоремы и соотношения расширят ваши представления об отрезках и углах, параллельности и перпендикулярности прямых на плоскости.

В процессе решения задач и доказательства теорем о свойствах треугольников вам предстоит освоить важные геометрические методы, которые помогут в ходе дальнейшего изучения геометрии.

Значимость невырожденных треугольников

Невырожденные треугольники являются основным строительным блоком геометрии и имеют большое значение в различных научных и практических областях. Они широко используются в архитектуре, инженерии, физике, графике и других науках.

Вот несколько основных причин, почему невырожденные треугольники являются важными:

1. Определение формы и размера: Невырожденные треугольники обладают четко определенной формой и размером. Используя их в качестве основного элемента для построения, архитекторы и инженеры могут создавать прочные и устойчивые сооружения. Например, пирамиды в Египте и готические соборы в Европе строятся на основе треугольников.
2. Вычисления и измерения: Треугольники являются одной из наиболее изученных геометрических фигур. Их свойства и формулы используются для вычислений и измерений в различных областях. Например, в геодезии треугольники используются для определения расстояний и углов на земной поверхности.
3. Графическое моделирование и анимация: Треугольники используются как основные элементы в компьютерной графике и анимации. В трехмерной графике объекты обычно представляются в виде множества треугольников, которые затем обрабатываются компьютером для создания реалистичных изображений и анимации.
4. Триангуляция: Треугольники играют важную роль в геометрии и алгоритмах триангуляции. Триангуляция представляет собой разбиение геометрической фигуры на невырожденные треугольники. Этот процесс используется в различных областях, таких как картография, сеточное моделирование и компьютерная графика.
5. Перспектива и пропорции: Треугольники используются для создания эффекта перспективы и определения пропорций в изображении. В искусстве и дизайне треугольники могут использоваться для создания глубины и тримерного вида, а также для соблюдения пропорций и гармонии в композиции.

Таким образом, невырожденные треугольники играют важную роль в различных областях, от строительства и наук о материалах до компьютерной графики и искусства. Понимание и использование треугольников позволяют нам лучше понять и описать мир вокруг нас.

Решение задач

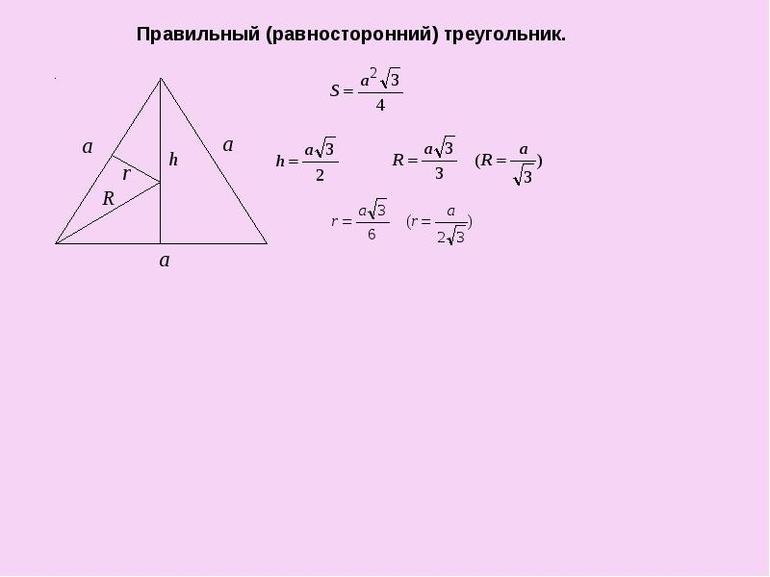
Чтобы уметь решать различные задания, связанные с треугольником, нужно помнить всего несколько формул. Но понадобится знать, что углы в фигуре равны друг другу и составляют 60 градусов. Часто придётся применять и теорему Пифагора. Вот некоторые из типовых заданий, используемые при обучении школьников в седьмом классе:

1. Какой будет радиус вписанной в правильный треугольник окружности, если его высота равняется 9 см. Зная свойство фигуры, решить задачу можно за пару секунд. Так как радиус равен 1/3 высоты, ответом на задачу будет: r = h / 3 = 9 / 3 = 3 см.
2. Сторона равностороннего треугольника равняется корню из трёх. Определить диаметр описанной окружности. Известно, что отношение синуса к противолежащему углу составляет 2R. Следовательно: R = a / 2 * sin (a) = √‎3 * 2 / 2 * √‎3 = 1.
3. Вокруг треугольной фигуры со стороной 8 √‎3 описан круг. Узнать его радиус. Эта задача в 2 действия. Используя формулу для нахождения вписанного радиуса и определение r = R / 2 можно записать: R = 2 * a * √‎3 / 6 = 2 * 8 * √‎3 * √‎3 / 6 = 2 * 4 = 8.
4. Пусть имеется квадрат, вокруг которого описана окружность. В ней так же располагается правильный треугольник. Периметр треугольной фигуры равен 9 √‎ 6. Нужно вычислить сумму всех сторон квадрата. На первом шаге необходимо определить длину боковой грани треугольника. Найти её можно по формуле: a = 3 √‎6. Теперь возможно рассчитать радиус описанной окружности: a = R * √‎3. Выполнив подстановку, найти ответ несложно: R = 3 √‎6 / √‎3 = 3 * √‎2. На третьем шаге можно выяснить, чему равняется сторона четырёхугольника. В этом поможет равенство: 3 √‎2 = (n √‎2) / 2. Отсюда n = 6. Значит, периметр квадрата равняется: P = 4 * 6 = 24.

Следует отметить, что выучить наизусть все формулы сложно, поэтому обычно используют логическое мышление и теоремы синусов-косинусов. Учитывая, что любой угол в равностороннем треугольнике равен 60 градусов практически любую формулу вывести можно самостоятельно.

Важность невырожденного треугольника для измерений

Один из основных аспектов, в котором невырожденные треугольники используются для измерений — это в геодезии. Геодезические измерения треугольников используются для определения расстояний и углов на больших расстояниях. Невырожденные треугольники служат основой для создания сетей измерений, которые необходимы для картографических и геодезических работ. Благодаря свойству невырожденности, треугольники позволяют точно определить положение географических объектов и создать точные карты.

В физике и инженерии также пользуются невырожденными треугольниками для измерений. Они используются, например, для измерения угловых скоростей и ускорений вращающихся объектов. Используя свойства невырожденных треугольников и принципы треугольной геометрии, физики и инженеры могут точно определить и измерить углы и расстояния траектории движения объекта.

Невырожденные треугольники также используются в строительстве и архитектуре для измерения и построения угловых структур. Они могут быть использованы для определения углов расположения стен, потолков, и других элементов здания

Создание точных и пропорциональных угловых структур важно для обеспечения качества и прочности конструкций

Таким образом, невырожденный треугольник играет важную роль в измерениях в различных областях науки и техники. Свойства невырожденного треугольника позволяют точно определить расстояния, углы и другие параметры, что является необходимым для создания точных карт, измерения физических величин и построения прочных и устойчивых конструкций.

Нормированное векторное пространство

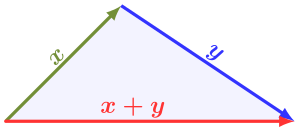Неравенство треугольника для норм векторов.

В нормированное векторное пространство V, одно из определяющих свойств норма это неравенство треугольника:

‖Икс+у‖≤‖Икс‖+‖у‖∀Икс,у∈V{ displaystyle displaystyle | x + y | leq | x | + | y | quad forall , x, y in V}

то есть норма не больше суммы норм двух векторов. Это также называется субаддитивность. Чтобы любая предлагаемая функция вела себя как норма, она должна удовлетворять этому требованию.

Если нормированное пространство евклидов, или, в более общем смысле, строго выпуклый, тогда ‖Икс+у‖=‖Икс‖+‖у‖{ Displaystyle | х + у | = | х | + | у |} если и только если треугольник, образованный Икс, у, и Икс + у, является вырожденным, то естьИкс и у находятся на одном луче, т.е. Икс = 0 или у = 0, илиИкс = α y для некоторых α > 0. Это свойство характеризует строго выпуклые нормированные пространства, такие как ℓ_п пространства с 1 < п < ∞. Однако есть нормированные пространства, в которых это неверно. Например, рассмотрим самолет с ℓ₁ норма ( Манхэттенское расстояние ) и обозначить Икс = (1, 0) и у = (0, 1). Тогда треугольник, образованныйИкс, у, и Икс + у, невырожден, но

‖Икс+у‖=‖(1,1)‖=|1|+|1|=2=‖Икс‖+‖у‖.{ Displaystyle | х + у | = | (1,1) | = | 1 | + | 1 | = 2 = | х | + | у |.}

Примеры норм

Абсолютное значение как норма для реальная линия. Чтобы быть нормой, неравенство треугольника требует, чтобы абсолютная величина удовлетворять для любых реальных чисел Икс и у:

|Икс+у|≤|Икс|+|у|,{ Displaystyle | х + у | Leq | х | + | у |,}

что он делает.

Доказательство:

−|Икс|≤Икс≤|Икс|{ displaystyle — left vert x right vert leq x leq left vert x right vert}

−|у|≤у≤|у|{ displaystyle — left vert y right vert leq y leq left vert y right vert}

После добавления

−(|Икс|+|у|)≤Икс+у≤|Икс|+|у|{ Displaystyle — ( влево верт х вправо верт + влево верт у вправо верт) Leq х + у Leq влево верт х вправо верт + влево верт у вправо vert}

Используйте тот факт, что |б|≤а⇔−а≤б≤а{ displaystyle left vert b right vert leq a Leftrightarrow -a leq b leq a}(с участием б заменяется Икс+у и а от |Икс|+|у|{ displaystyle left vert x right vert + left vert y right vert}), у нас есть

|Икс+у|≤|Икс|+|у|{ Displaystyle | х + у | Leq | х | + | у |}

Неравенство треугольника полезно в математический анализ для определения наилучшей верхней оценки размера суммы двух чисел в терминах размеров отдельных чисел.

Существует также более низкая оценка, которую можно найти с помощью обратное неравенство треугольника в котором говорится, что для любых действительных чисел Икс и у:

|Икс−у|≥||Икс|−|у||.{ displaystyle | x-y | geq { bigg |} | x | — | y | { bigg |}.}

Внутренний продукт как норма в внутреннее пространство продукта. Если норма возникает из внутреннего произведения (как в случае евклидовых пространств), то неравенство треугольника следует из Неравенство Коши – Шварца следующим образом: данные векторы Икс{ displaystyle x} и у{ displaystyle y}, и обозначив внутренний продукт как ⟨Икс,у⟩{ Displaystyle langle х, у rangle}:

‖Икс+у‖2{ Displaystyle | х + у | ^ {2}}	=⟨Икс+у,Икс+у⟩{ displaystyle = langle x + y, x + y rangle}
	=‖Икс‖2+⟨Икс,у⟩+⟨у,Икс⟩+‖у‖2{ displaystyle = | x | ^ {2} + langle x, y rangle + langle y, x rangle + | y | ^ {2}}
	≤‖Икс‖2+2|⟨Икс,у⟩|+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | langle x, y rangle | + | y | ^ {2}}
	≤‖Икс‖2+2‖Икс‖‖у‖+‖у‖2{ Displaystyle Leq | х | ^ {2} +2 | х | | у | + | у | ^ {2}} (по неравенству Коши – Шварца)
	=(‖Икс‖+‖у‖)2{ Displaystyle = влево ( | х | + | у | вправо) ^ {2}}.

Неравенство Коши – Шварца превращается в равенство тогда и только тогда, когда Икс и улинейно зависимы. Неравенство⟨Икс,у⟩+⟨у,Икс⟩≤2|⟨Икс,у⟩|{ displaystyle langle x, y rangle + langle y, x rangle leq 2 | langle x, y rangle |}превращается в равенство для линейно зависимых Икс{ displaystyle x} и у{ displaystyle y}тогда и только тогда, когда один из векторов Икс или у это неотрицательный скаляр другого.

Извлечение квадратного корня из окончательного результата дает неравенство треугольника.

п-норма: обычно используемой нормой является п-норма:

‖Икс‖п=(∑я=1п|Икся|п)1п ,{ Displaystyle | х | _ {p} = left ( sum _ {i = 1} ^ {n} | x_ {i} | ^ {p} right) ^ {1 / p} ,}

где Икс_я компоненты вектора Икс. Для п = 2 то п-норма становится Евклидова норма:

‖Икс‖2=(∑я=1п|Икся|2)12=(∑я=1пИкся2)12 ,{ Displaystyle | х | _ {2} = влево ( сумма _ {я = 1} ^ {п} | х_ {я} | ^ {2} вправо) ^ {1/2} = влево ( sum _ {i = 1} ^ {n} x_ {i} ^ {2} right) ^ {1/2} ,}

который Теорема Пифагора в п-размеры, очень частный случай, соответствующий внутренней норме продукта. Кроме случая п = 2, то п-норма не внутренняя норма продукта, потому что она не удовлетворяет закон параллелограмма. Неравенство треугольника для общих значений п называется Неравенство Минковского. Он принимает вид:

‖Икс+у‖п≤‖Икс‖п+‖у‖п .{ displaystyle | x + y | _ {p} leq | x | _ {p} + | y | _ {p} .}

Вписанная окружность треугольника

У вписанной окружности треугольника есть ряд свойств:

1. Радиус вписанной окружности равен половине длины стороны треугольника, с которой он соприкасается.
2. Центр вписанной окружности является точкой пересечения трех биссектрис треугольника, то есть линий, которые делят углы треугольника пополам.

Для проверки равнобедренности треугольника можно проверить, совпадают ли проекции вершин треугольника на сторону, к которой они прилегают, и проекция центра вписанной окружности. Если проекции совпадают, то треугольник является равнобедренным.

Существует также классификация треугольников по типу вписанной окружности:

1. Треугольник, в котором центр вписанной окружности совпадает с центром описанной окружности, называется остроугольным треугольником.
2. Треугольник, в котором центр вписанной окружности лежит внутри треугольника, но не совпадает с центром описанной окружности, называется прямоугольным треугольником.
3. Треугольник, в котором центр вписанной окружности лежит вне треугольника, называется тупоугольным треугольником.
4. Если треугольник равнобедренный и равносторонний, то вписанная окружность будет совпадать с описанной окружностью.

Из формул для треугольников можно также найти радиус вписанной окружности и его длину:

• Радиус вписанной окружности можно найти по формуле: ( r = frac{{ ext{{площадь треугольника}}}}{{ ext{{периметр треугольника}}}} ).
• Длина окружности можно найти по формуле: ( L = 2 pi r ), где ( pi ) — это число пи.

Таким образом, вписанная окружность треугольника является важным элементом его геометрии. Она обладает рядом свойств, которые можно использовать для классификации треугольников и вычисления различных характеристик.

[править] Свойства и особенности треугольников

Трём точкам пространства, не лежащим на одной прямой (и образуемому ими невырожденному треугольнику), обязательно соответствует одна и только одна плоскость. Это весьма уникально — так как меньшему количеству точек соответствуют прямая и точка, а уже четыре точки могут находится вне единой плоскости.

Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве. Процесс разбиения на треугольники называется триангуляция.

Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Треугольник, когда не вырожден — всегда выпуклый многоугольник.

Для треугольника всегда существует одна вписанная и одна описанная окружность.

Слайд 13 Замечательные прямые треугольника Замечательные прямые треугольника — прямые, местоположение которых однозначно

определяется треугольником. Местоположение некоторых не зависит от того, в каком порядке

берутся стороны и вершины треугольника (например, прямая Эйлера). Местоположение же большинства зависит от того, в каком порядке берутся стороны и вершины треугольника.Обычно они расположены внутри треугольника, но и это не обязательно. В частности, высота может находиться и вне треугольника.Многие однотипные замечательные прямые треугольника при пересечении образуют замечательные точки треугольника. Например, на пересечении трех высот треугольника находится замечательная точка треугольника — ортоцентр.

В геометрии

Коническое сечение

Вырожденная коника — это коническое сечение (плоская кривая второй степени , определяемая полиномиальным уравнением второй степени), которая не может быть неприводимой кривой.

• A точкой, является вырожденная окружность, а именно, радиус 0.
• Линия — это вырожденный случай параболы, если парабола находится на касательная плоскость. В инверсной геометрии линия является вырожденным случаем окружности с бесконечным радиусом.
• Две параллельные линии также образуют вырожденную параболу.
• A отрезок можно рассматривать как вырожденный случай эллипса, в котором малая полуось переходит в ноль, а фокусы переходят в конечных точек, а эксцентриситет переходит в единицу.
• Окружность можно представить как вырожденный эллипс, поскольку эксцентриситет приближается к нулю.
• Эллипс также может вырождаться в одну точку.
• A гипербола может вырождаться в две линии, пересекающиеся в точке, через семейство гипербол, имеющих эти линии как общие асимптоты.

Треугольник

A вырожденный треугольник имеет коллинеарные вершины и нулевую площадь и, таким образом, совпадает с отрезком, покрытым дважды (если три вершины не равны; в противном случае треугольник вырождается в одну точку). Если три вершины попарно различны, он имеет два угла 0 ° и один угол 180 °. Если две вершины равны, у него один угол 0 ° и два неопределенных угла.

Прямоугольник

• Отрезок линии — это вырожденный случай прямоугольника , длина стороны которого равна 0.
• Для любого непустого подмножества S ⊆ {1, 2,…, n} {\ displaystyle S \ substeq \ {1,2, \ ldots, n \}}, существует ограниченный выровненный по оси вырожденный прямоугольник

  R ≜ {x ∈ R n: xi = ci (для i ∈ S) и ai ≤ xi ≤ bi (для i ∉ S)} {\ displaystyle R \ Triangleq \ left \ {\ mathbf {x} \ in \ mathbb {R} ^ {n}: x_ {i} = c_ {i} \ ({\ text {for}} i \ in S) {\ text {и}} a_ {i} \ leq x_ {i} \ leq b_ {i} \ ({\ text {for}} i \ notin S) \ right \}}

  где x ≜ {\ displaystyle \ mathbf {x} \ треугольник q \ left }и ai, bi, ci {\ displaystyle a_ {i}, b_ {i}, c_ {i}}являются постоянными (с ai ≤ bi {\ displaystyle a_ {i} \ leq b_ {i }}для всех i {\ displaystyle i}). Количество вырожденных сторон R {\ displaystyle R}- это количество элементов подмножества S {\ displaystyle S}. Таким образом, может быть всего одна вырожденная «сторона» или целых n {\ displaystyle n}(в этом случае R {\ displaystyle R}сводится к одноэлементной точке).

Выпуклый многоугольник

A выпуклый многоугольник является вырожденным, если хотя бы две последовательные стороны совпадают хотя бы частично, или хотя бы одна сторона имеет нулевую длину, или хотя бы один угол равен 180 °. Таким образом, вырожденный выпуклый многоугольник с n сторонами выглядит как многоугольник с меньшим числом сторон. В случае треугольников это определение совпадает с тем, что было дано выше.

Выпуклый многогранник

A выпуклый многогранник вырожден, если либо две смежные грани копланарны, либо два ребра являются выровнен. В случае тетраэдра это эквивалентно тому, что все его вершины лежат в одной плоскости, что дает ему объем нуля.

Стандартный тор

В контекстах, где разрешено самопересечение, сфера представляет собой вырожденный стандартный тор, ось вращения которого проходит через центр образующий круг, а не за его пределами.

[править] Свойства и особенности треугольников

Трём точкам пространства, не лежащим на одной прямой (и образуемому ими невырожденному треугольнику), обязательно соответствует одна и только одна плоскость. Это весьма уникально — так как меньшему количеству точек соответствуют прямая и точка, а уже четыре точки могут находится вне единой плоскости.

Треугольник — это часть плоскости, ограниченная минимально возможным количеством сторон. Любой многоугольник можно точно разбить на треугольники, лишь связав его вершины отрезками, не пересекающими его стороны. С некоторым приближением, на треугольники можно разбить поверхность любой формы, как на плоскости так и в пространстве. Процесс разбиения на треугольники называется триангуляция.

Существует раздел математики, целиком посвящённый изучению закономерностей треугольников — Тригонометрия.

Треугольник, когда не вырожден — всегда выпуклый многоугольник.

Для треугольника всегда существует одна вписанная и одна описанная окружность.

Сумма углов треугольника

В невырожденном треугольнике существуют разные типы углов:

1. Острые углы — углы, меньшие 90°;
2. Прямой угол — угол, равный 90°;
3. Тупой угол — угол, больший 90°, но меньший 180°.

Теорема о сумме углов треугольника утверждает, что в невырожденном треугольнике сумма углов всегда равна 180°. Это свойство можно доказать несколькими способами, например через параллельные линии или с использованием проекций.

Сумма углов в треугольнике можно найти с помощью формулы α + β + γ = 180°, где α, β и γ — углы треугольника.

Пользуясь этой формулой, можно определить тип треугольника по его углам:

• Треугольник с тремя острыми углами называется остроугольным, если все его углы меньше 90°;
• Треугольник с одним прямым углом называется прямоугольным;
• Треугольник с одним тупым углом называется тупоугольным.

Кроме того, сумма углов треугольника связана с его высотой. В прямоугольных треугольниках, высота проходит через прямой угол, а в остроугольных и тупоугольных треугольниках, высоты опускаются из вершин на стороны треугольника.

Также, сумма углов треугольника связана с площадью треугольника. С помощью высоты можно вычислить площадь треугольника по формуле S = 1/2 * a * h, где a — основание треугольника, h — высота. Или можно воспользоваться формулой S = 1/2 * b * c * sin(α), где b и c — боковые стороны треугольника, α — угол между ними.

В общем случае, треугольник можно классифицировать по различным свойствам, таким как равные стороны, равные углы, соотношение между сторонами внутри треугольника (например, теорема Пифагора), подобие с другими треугольниками и т.д.

Способы определения типов невырожденных треугольников:

Способ 1: Определение по длинам сторон

Если треугольник имеет три стороны, причем каждая сторона неравна нулю, то его можно классифицировать по длинам сторон.

• Равносторонний треугольник — все стороны равны между собой.
• Разносторонний треугольник — все стороны различны.
• Равнобедренный треугольник — у треугольника есть две равные стороны.

Способ 2: Определение по углам

Углы треугольника также могут помочь определить его тип:

• Остроугольный треугольник — все углы треугольника острые (меньше 90 градусов).
• Прямоугольный треугольник — треугольник имеет один прямой угол (равный 90 градусов).
• Тупоугольный треугольник — треугольник имеет один тупой угол (больше 90 градусов).

Способ 3: Определение по соотношению длин сторон и углов

Существуют также более сложные условия, при которых возможно определение типа треугольника. Например, если известно, что сторона треугольника в 4 раза больше, чем ордината основания высоты, а один его угол составляет 60 градусов, то такой треугольник называется 30-60-90 треугольником.

Зная эти способы определения, можно точно классифицировать невырожденный треугольник по его свойствам и характеристикам.

Что такое треугольник

Рассмотрим понятие треугольника. Пусть на плоскости дана трехзвенная замкнутая ломаная. Тогда эта ломаная разделяет множество оставшихся точек плоскости на ограниченную и неограниченную фигуры. При этом ограниченная фигура называется частью плоскости, ограниченной данной ломаной. Например, на рисунке 59, а изображена часть плоскости, ограниченная трехзвенной замкнутой ломаной ABC.

Определение. Треугольником называется геометрическая фигура, состоящая из трехзвенной замкнутой ломаной и части плоскости, ограниченной этой ломаной.

Вершины ломаной называются вершинами треугольника, а звенья ломаной — сторонами треугольника.

Точки треугольника, не принадлежащие его сторонам, называются внутренними.

Треугольник, вершинами которого являются точки А, В и С, обозначается следующим образом:

АВС
BСА
CАВ

На рисунке 59, а изображен треугольник ABC. Точки А, В и С — вершины этого треугольника, а отрезки AB, ВС и АС — его стороны. На рисунке 59, B показан треугольник AFD, содержащийся в грани куба.

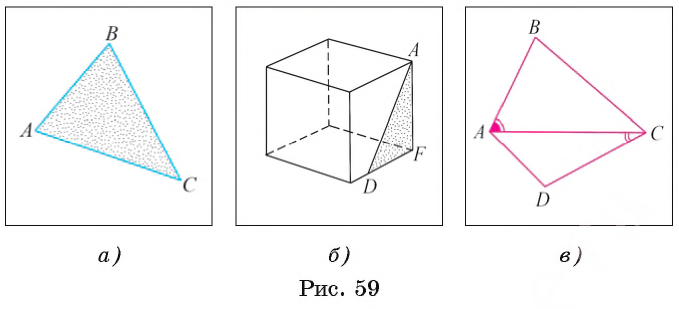
Углы АBС, АСВ и САВ (см. рис. 59, а) называются внутренними углами треугольника ABC или просто углами треугольника. Иногда они обозначаются одной буквой:

A,
B,
CСтороны и углы треугольника называются его элементами.

На рисунке 59, в изображены треугольники ABC и ACD, у которых общая сторона АС. Угол ВАС — внутренний угол треугольника ВАС,

ACD

Периметром треугольника называется сумма длин всех его сторон. Периметр треугольника ABC обозначается P_ABC.

Конструкции, имеющие треугольную форму, применяются при строительстве архитектурных сооружений, мостов и жилых зданий. Например, при постройке крыш некоторых домов используются стропила, имеющие форму треугольников (рис. 60, а).

Для треугольников, как и любых геометрических фигур, определяется понятие их равенства.

Два треугольника называются равными, если их можно совместить наложением, т. е. можно совместить их вершины, стороны и углы.

Рассмотрим пример. Если лист бумаги, имеющий форму прямоугольника, разрезать на две части, как показано на рисунке 60, б, то мы получим модели равных треугольников. Непосредственно можно убедиться, что полученные части можно наложить одна на другую так, что они совместятся.

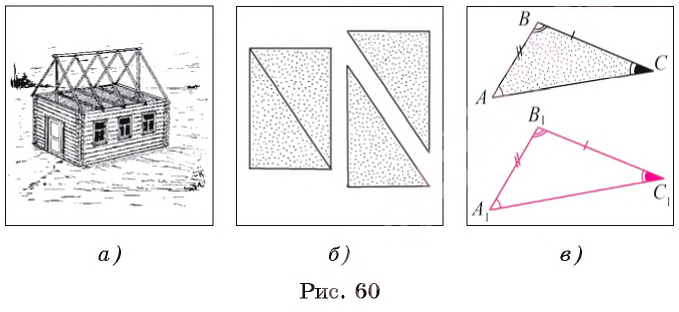
Два равных треугольника ABC и A₁B₁C₁(рис. 60, в) можно совместить так, что попарно совместятся их вершины, стороны и углы. Другими словами, если два треугольника равны, то стороны и углы одного треугольника соответственно равны сторонам и углам другого треугольника. Подчеркнем, что:

• в равных треугольниках против соответственно равных сторон лежат равные углы;
• в равных треугольниках против соответственно равных углов лежат равные стороны.

Например, в равных треугольниках ABC и A₁B₁C₁, изображенных на рисунке 60, в, против равных сторон ВС и В₁С₁лежат равные углы А и А₁. Против равных углов С и С₁ лежат равные стороны AB и A₁B₁.

Если треугольники ABC и A₁B₁C₁ равны, то это обозначается следующим образом:

ABC
A₁B₁C₁

Заметим, что для установления равенства треугольников необязательно их совмещать один с другим, а достаточно сравнить некоторые их элементы (стороны и углы).

Для доказательства равенства треугольников пользуются соответствующими теоремами (признаками), которые позволяют на основании равенства некоторых элементов треугольников делать вывод о равенстве самих треугольников.

Значение понятия «Невырожденный треугольник»

Невырожденный треугольник — это треугольник, который имеет конечные стороны и углы, а также положительную площадь. Такой треугольник является основным объектом изучения геометрии и математики.

Значит, треугольник, который не является невырожденным, будет иметь одну или несколько из следующих характеристик:

• Одна или несколько сторон имеют нулевую длину. В этом случае треугольник превращается в отрезок или точку.
• Одна или несколько сторон имеют отрицательную длину. Это может происходить, когда точки, задающие стороны треугольника, расположены в неправильном порядке.
• Сумма длин двух сторон меньше третьей стороны. Такой треугольник называется вырожденным, и он не может существовать в двумерном пространстве.
• Один или несколько углов равны 0 или 180 градусов. Такие углы называются вырожденными углами и не отличаются от прямой линии или плоскости.

Имея эти определения в виду, мы можем утверждать, что для треугольника с конечными сторонами и положительной площадью справедливо понятие «невырожденный треугольник». Это базовое понятие является основой для изучения свойств и характеристик треугольников в геометрии.

Основные характеристики невырожденного треугольника

Что значит невырожденный треугольник? Невырожденный треугольник — это треугольник, у которого все три стороны положительной длины и никакие три точки, задающие его вершины, не лежат на одной прямой.

Вот основные характеристики, которые отличают невырожденный треугольник:

• Три стороны: невырожденный треугольник имеет три стороны, каждая из которых имеет положительную длину и является отрезком прямой между двумя вершинами.
• Три вершины: треугольник имеет три вершины, которые являются точками пространства или плоскости. Вершины образуют углы друг с другом.
• Три угла: треугольник состоит из трех углов, которые образуются между сторонами. Сумма всех углов в невырожденном треугольнике равна 180 градусам.
• Площадь: невырожденный треугольник имеет площадь, которая можно вычислить с использованием формулы Герона или других методов.
• Периметр: периметр невырожденного треугольника — это сумма всех его сторон. Он также может быть вычислен с помощью известных значений длин сторон.

Невырожденный треугольник является одной из основных фигур в геометрии. Он имеет множество свойств и характеристик, которые могут быть использованы для изучения его свойств и применения в различных математических и физических задачах.

Различия невырожденного треугольника от вырожденного

Треугольник — это геометрическая фигура, состоящая из трех отрезков, которые соединяются между собой в трех точках. Однако не все треугольники являются невырожденными, и это имеет свои особенности и значения.

Невырожденный треугольник (также известный как обычный треугольник) — это треугольник, у которого все три стороны имеют разную длину и все три угла не равны нулю и не равны 180 градусов. Невырожденный треугольник значит, что он имеет достаточно размеров и формы, чтобы считаться полноценным и функциональным треугольником.

Основное отличие невырожденного треугольника от вырожденного заключается в его свойствах и определениях. Невырожденный треугольник имеет три разные стороны и три угла, которые в сумме равны 180 градусов. Каждая сторона невырожденного треугольника соединяет две точки, и каждый угол образуется между двумя сторонами. Такой треугольник может быть измерен и описан с помощью геометрических формул и правил.

В то же время, вырожденный треугольник имеет особые свойства и определения. Он представляет собой треугольник, у которого все три стороны соединены в одной точке, а все три угла равны нулю или 180 градусов. Это значит, что его стороны и углы не образуют полноценной фигуры у треугольника и не могут быть измерены с помощью геометрических формул.

Таким образом, различия между невырожденным и вырожденным треугольниками заключаются в их свойствах и определениях. Невырожденный треугольник является полноценной геометрической фигурой с тремя разными сторонами и углами в сумме, равной 180 градусов, в то время как вырожденный треугольник не обладает такими свойствами и не может быть измерен с помощью геометрических формул.

Особые линии и точки

Медиана, высота и биссектриса — 3 замечательные линии любого треугольника. Представляют они собой внутренние отрезки, построенные из углов на противоположные стороны. Линия, соединяющая вершину с серединой противоположной грани, называется медианой. Луч, разделяющий угол на 2 равные части — это биссектриса, а перпендикуляр, построенный к стороне — высота.

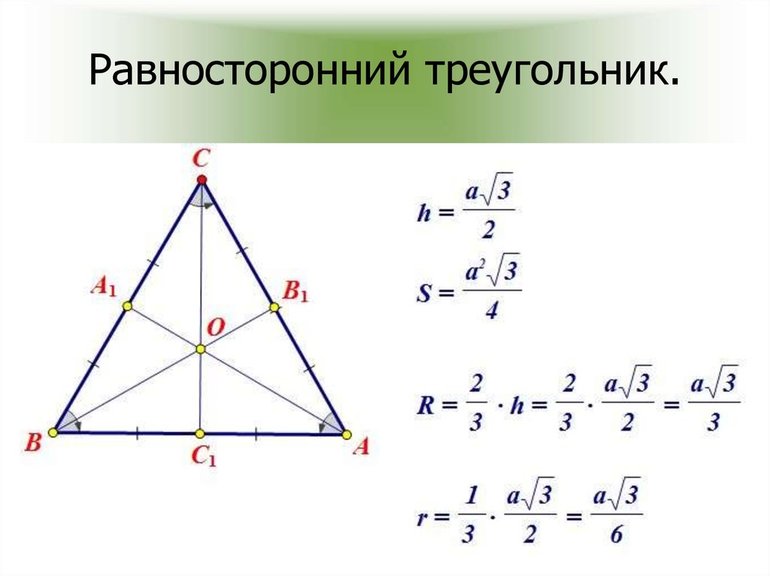
В любом правильном треугольнике можно начертить 3 отрезка. Если отложить медиану, а потом биссектрису и высоту, можно заметить, что эти линии совпадут. Эта особенность и есть замечательным свойством равностороннего многоугольника, то есть если в любой другой трёхугольной фигуре можно построить 12 особых линий, то в рассматриваемом только 3.

Доказать это утверждение можно следующим образом: пусть имеется треугольник АВС, в котором проведена высота ВH. Далее, рассуждения нужно построить так:

1. Отрезок BH перпендикулярен прямой AC по построению.
2. Точка H разделяет отрезок AC на AD и CD. Если это утверждение будет верным, это означает, что построенная высота BH будет медианой треугольника.
3. Отрезок BH создаёт в многоугольнике 2 угла — ∠ABH и ∠CBH. При верности этого утверждения можно утверждать, что отрезок BH является биссектрисой.

Если создать зеркальное отражение треугольнику и совместить его с оригинальным, все углы попарно совместятся. Совпадут и стороны. Так как ВH — высота, она перпендикуляр. Значит, в точке H отрезок образует прямой угол с боковой гранью AC. Отсюда следует, что образованные треугольники AHB и CBH прямоугольные.

Они являются равными по общей гипотенузе и острому углу. Это следует из того, что правильный многоугольник — частный случай равнобедренного. Так как треугольники совпадают, у них одинаковые углы ABH и CBH. Причём они смежные, поэтому BH — биссектриса. В то же время точка H делит AC на 2 равных отрезка, значит, BH — медиана.

Топ вопросов за вчера в категории образование

Образование 16.09.2023 23:41 2082 Ткачёв Витя.

Какое проверочное слово к слову ОГОРОД?

Ответов: 1

Образование 06.10.2023 16:43 831 Романов Ярослав.

Как правильно гулять» по лесу» или в» лесу»?

Ответов: 1

Образование 26.08.2023 14:06 2182 Пинчук Никита.

Какие фрукты начинаются на букву «Р»?

Ответов: 1

Образование 11.10.2023 21:09 1383 Ситникова Евгения.

Какое проверочное слово к слову ПРЕДПОЛАГАТЬ?

Ответов: 1

Образование 01.09.2023 05:01 2059 Зонова Виктория.

Какие фрукты начинаются на букву «Д»?

Ответов: 1

Образование 28.10.2023 10:34 1956 Угланова Яна.

Как решить: Для перевозки груза потребовалось 24 машины грузоподъём. 7,5 т?

Ответов: 1

Образование 10.10.2023 17:31 656 Швецов Степан.

Какое проверочное слово к слову иссЯкать?

Ответов: 1

Образование 04.10.2023 07:56 225 Самохвалов Ярослав.

Много очистков или очисток, как правильно?

Ответов: 1

Образование 07.11.2023 10:30 229 Ширяев Данил.

Какое проверочное слово к слову СОСТАВЛЯТЬ?

Ответов: 1

Образование 02.09.2023 05:24 1273 Салымгереев Акылбек.

Как правильно: по получении или по получению?

Ответов: 1