Действительные числа

Примеры использования недействительных и комплексных чисел

1. Электрические цепи:

Недействительные числа могут возникать в расчетах электрических цепей. Например, при расчете последовательного соединения активного сопротивления, индуктивности и емкости, возможно получение недействительного сопротивления. Для таких случаев необходимо использовать комплексные числа.

R	JL	JC	W	Z
200	500	50	-153.846j

2. Квадратные уравнения:

Квадратные уравнения могут иметь комплексные корни, формирующие некоторые закономерности и принципы. Например, сумма корней квадратного уравнения равна -b/a, где b – коэффициент при x, a – коэффициент при x². Это правило работает независимо от наличия или отсутствия комплексных корней. Если комплексных корней нет, то сумма корней квадратного уравнения равна -b/a.

3. Механика квантовых систем:

В механике квантовых систем, таких как атом, молекула, частица, комплексные числа используются для описания волновой функции этих частиц. Квантовая механика утверждает, что все эти частицы имеют двойственную природу: иногда они ведут себя как частицы, а иногда как волны. Эта двойственность отражается в использовании комплексных чисел.

Виды преобразования выражений

Иррациональные выражения содержат операцию извлечения корня. Это особые записи, состоящие из радикалов и знаков алгебраических действий.

Во время преобразования таких выражений нельзя допускать сужения области допустимых значений. С ними разрешается проводить любые из основных тождественных преобразований:

• раскрытие скобок;
• группировка подобных множителей и слагаемых;
• перестановка множителей и слагаемых;
• замена разности суммой.

Замена исходной записи

Подкоренное выражение можно заменить тождественно равным, то есть математической записью, значение которой будет равно исходному. Следует учитывать, что равенство должно соблюдаться при любых допустимых значениях переменных, которые входят в состав обоих выражений.

Использование свойств корней

Для упрощения сложных выражений часто применяются свойства корней, к примеру, перемножение их степеней. Делать это необходимо в соответствии со специальными формулами.

Особое внимание при работе следует обращать на отрицательные числа и выражения с переменными. В ряде случаев для применения формул такие значения сначала придётся привести к тождественно равным, которые подойдут для дальнейшего использования свойств корней.. Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом

После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.

Внесение множителя под знак корня — это преобразование произведения, в котором лишь один из множителей находится под знаком радикала со степенью, выраженной натуральным числом. После замены выражения под корнем будут находиться все множители, составляющие произведение, но оно останется равным исходному.

Изменение дробей

Иррациональные математические записи могут содержать дроби с радикалами в делимом или делителе. С ними разрешается проводить любые действия, относящиеся к основным преобразованиям дробных чисел:

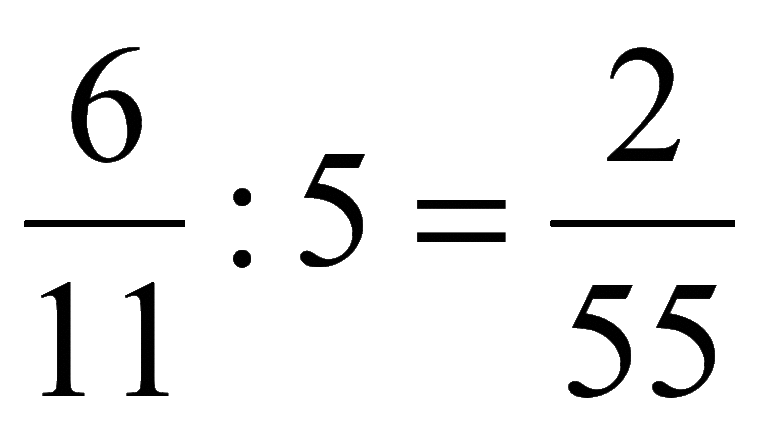
• Отдельное вычисление выражений, находящихся в числителе и знаменателе.
• Изменение знака перед дробью, которое влечёт за собой перемену знаков делимого и делителя.
• Проведение сокращения дроби, если это является возможным и целесообразным. Зачастую перед тем как сократить значение, необходимо вычислить множители, составляющие числитель и знаменатель. Иногда перед сокращением можно заменить переменную, чтобы исходная иррациональная величина стала более удобной рациональной.
• Приведение к новому знаменателю посредством умножения делимого и делителя на один дополнительный множитель. При этом действии следует учитывать, что выполнение сокращения или приведения к новому знаменателю возможно только на область допустимого значения переменных для исходного числа.

Избавление от иррациональности в знаменателе

Освобождение от иррациональности в знаменателе представляет собой преобразование дроби путём её замены на тождественно равную с делителем, не содержащим корней и степеней. Для этого необходимо последовательно провести два действия:

• Умножение числителя и знаменателя на значение, которое отличается от 0.
• Преобразование выражения, ставшего новым делителем.

Переход к степеням

Переход от радикалов к степеням осуществляется на основе равенства, давшего определение степени, которая имеет рациональный показатель. При этом используется следующая формула:

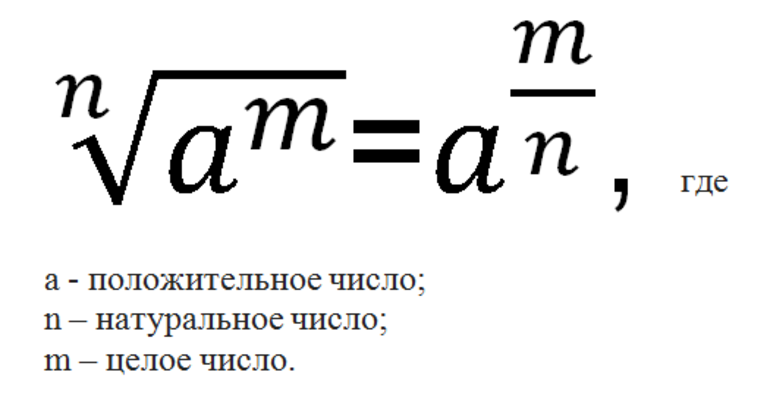
Если же величина под радикалом отрицательная или там находится выражение с переменными, то перед использованием формулы подкоренное значение необходимо преобразовать. Для этого следует применять свойства степеней.

Число «е» и его иррациональность

Иррациональность числа «е» была доказана в 1873 году швейцарским математиком Шарлем Эрмитом. Он показал, что «е» не может быть выражено в виде дроби и не является алгебраическим числом.

Число «е» появляется во многих разделах математики и физики, включая ряды Тейлора, дифференциальные уравнения, комплексный анализ и вероятность. Оно также имеет связь с экспоненциальной функцией, график которой представляет собой параболу, проходящую через точку (1, е).

Доказательство иррациональности числа «е» основано на его ряде Маклорена, который имеет вид:

1. е = 1 + 1/1! + 1/2! + 1/3! + 1/4! + …

Данный ряд является бесконечной суммой, где каждый член ряда равен обратному факториалу натурального числа.

Доказательство иррациональности заключается в том, что ряд Маклорена для «е» является сходящимся рядом, но его сумма является иррациональным числом. Это было достигнуто путем анализа разности между приближенной и истинной суммами ряда Маклорена, которая стремится к нулю при неограниченном увеличении числа членов ряда.

Как определить недействительный аргумент?

Иногда при обсуждении или дебатах люди предлагают аргументы, которые не основаны на достоверных фактах или логических связях. Такие аргументы называются недействительными. Они могут быть ошибочными, искаженными или просто не имеющими базы

Чтобы успешно вести дискуссию и делать информированные выводы, важно различать действительные и недействительные аргументы

Существует несколько признаков, которые помогут определить недействительность аргумента:

1. Аргумент от авторитета	В этом случае, аргумент считается недействительным, если он основывается только на мнении какого-либо авторитетного лица без предоставления достаточной информации или фактических данных.
2. Ложное причинно-следственное утверждение	Это ошибка, когда говорят, что одно явление является причиной другого, в то время как нет научных доказательств или логической связи между ними.
3. Применение личных представлений	Недействительный аргумент заключается в использовании субъективных мнений или чувств вместо объективных фактов и доказательств.
4. Аргумент от неверной аналогии	В этом случае, сравнение двух явлений или ситуаций основывается на неправильной аналогии, что делает аргумент недействительным.

Иметь возможность распознавать недействительные аргументы позволяет лучше анализировать информацию и принимать обоснованные решения

Когда находите недействительный аргумент, важно быть готовым предоставить альтернативу на основе доступных фактов и логики

Правила сравнения

Иногда для решения математических задач необходимо провести сравнение иррациональных значений. При этом необходимо руководствоваться следующими правилами:

• Два числа с иррациональностью будут считаться равными при происхождении от измерения одной единицей двух равных величин. Эти величины обязательно должны содержать одинаковое количество единиц, десятых, сотых, тысячных долей и так далее. Таким образом, равные иррациональные значения должны выражаться в одинаковых цифрах.
• Если сравнивают два неравных значения, то большим будет считаться число, полученное в результате измерения большей величины. Указанная величина всегда содержит больше целых, или десятых, или сотых частей и так далее.

Для возведения иррациональной величины в степень необходимо возвести в неё значение под радикалом. Если величина корня равна степени, то в итоге число или выражение выносится из-под корня неизменным, поскольку возникают взаимно сокращающиеся действия.

https://youtube.com/watch?v=gCwNTZJAM1M

Если иррациональное выражение находится под корнем, то для его извлечения показатели радикалов умножают. Этот метод позволяет упрощать извлечение корней четвёртой, шестой, восьмой, девятой степени.

Иррациональные числа можно узнать по специальным буквам, используемым для их обозначения, или по написанию в виде десятичных дробей, не имеющих окончания. Выражения этого типа легко отличить по наличию радикала. С подобными значениями проводят те же действия, что и с другими вещественными числами. Их можно умножить, сложить, сравнить и так далее.

Иррациональные числа

Иррациональное число — это действительное число, которое нельзя записать в виде простой дроби:

  1,5 рационально, но π иррационально

Иррациональное означает

Давайте посмотрим, что делает число рациональным или иррациональным…

Рациональные числа

A Rational Число можно записать как 0003 Отношение двух целых чисел (т.е. простой дроби).

Пример: 1,5 является рациональным, поскольку его можно записать как отношение 3/2

Пример: 7 рационально, потому что его можно записать как отношение 7/1

Пример 0,333. .. (3 повторения) также является рациональным, поскольку его можно записать как отношение 1/3

Но некоторые цифры нельзя записать как отношение двух целых чисел…

…их называют Иррациональные Числа .

Пример:

π (Pi)

π  = 3,1415926535897932384626433832795… (и больше)

Мы не можем s записать простую дробь, которая равна Пи.

Популярное приближение 22 / ₇ = 3,1428571428571… близко, но неточное .

Еще одна подсказка заключается в том, что десятичная дробь продолжается вечно, не повторяясь.

Не может быть записан как дробь

Это иррационально потому что его нельзя записать как отношение (или дробь), не потому что это безумие!

Таким образом, мы можем определить, является ли число рациональным или иррациональным, попробовав записать число в виде простой дроби.

Пример:

9,5

9,5 = 19 2

Итак, это рациональное число (и поэтому не иррациональное )

Вот еще несколько примеров:

Номер

Как дробь
 
Рациональное или Иррациональное?
1,75
 
7 4

 
Рационал

.001
 
1 1000

 
Рационал

√2 (квадратный корень из 2)
 
?
 
Неразумно !

Квадратный корень из 2

Давайте посмотрим на квадратный корень из 2 более внимательно.

Когда мы рисуем квадрат размера «1», каково расстояние по диагонали?

Ответ: квадратный корень из 2 , который равен 1.4142135623730950…(и т.д.)

… на самом деле мы не может записать квадратный корень из 2, используя отношение двух чисел…

… (вы можете узнать , почему , на странице «Иррационально ли это?»)…

… и так мы знаем это иррациональное число .

		Пи — известное иррациональное число. Люди вычислили число Пи с точностью до квадриллиона знаков после запятой, но закономерности до сих пор нет. Первые несколько цифр выглядят так: 3.1415926535897932384626433832795 (и еще…)
		Число e (число Эйлера) — еще одно известное иррациональное число. Люди также вычислили e до большого количества знаков после запятой без какой-либо закономерности. Первые несколько цифр выглядят так:. 2,7182818284590452353602874713527 (и еще…)
		Золотое сечение — иррациональное число. Первые несколько цифр выглядят так: . 1.61803398874989484820… (и еще…)
		Многие квадратные корни, кубические корни и т. д. также являются иррациональными числами. Примеры: √3 1.7320508075688772935274463415059 (и т. д.) √99 9,9498743710661995473447982100121 (и т. д.)

Но √4 = 2 рационально, а √9 = 3 рационально.

… так что не все корни иррациональны.

Примечание по умножению иррациональных чисел

Взгляните на это:

• π × π = π 2 известно, что иррационально
• Но √2 × √2 = 2 равно рациональному

Так что будьте осторожны… умножение иррациональных чисел может дать рациональное число!

Забавные факты….

По-видимому Гиппас (один из учеников Пифагора) открыл иррациональные числа при попытке записать квадратный корень из 2 в виде дроби (считается, что с помощью геометрии). Вместо этого он доказал квадратный корень из 2·9.0093 нельзя было записать в виде дроби, поэтому иррационально .

Но последователи Пифагора не могли принять существование иррациональных чисел, и говорят, что Гиппас был утоплен в море в наказание богов!

434 435 1064 2022 3987 1065 3988 2023 2990 2991

Подмножества чисел

Действительные числа состоят из подмножеств, каждое из которых следует рассмотреть отдельно:

• Натуральные числа. Натуральные числа были так названы еще древними греками. Натуральные или природные – это первые числа, которые придумало человечество. Их до сих пор используют для счета на рынке или в магазине. Там, где не нужны сложные и долгие вычисления: для простого счета используется именно эта категория чисел.
• Целые числа. Сюда входят помимо натуральных, еще и число ноль и отрицательные числа, но только целые. Дроби в эту категорию не входят.
• Рациональные числа. Сюда входят все целые и натуральные числа, а так же любые дроби.
• Иррациональные числа. Это подмножество не пересекается с рациональными числами, но так же относится к действительным числам.

Обратите внимание, что число 0 для счета не используется, то есть оно не относится к натуральным числам. Само число 0 было изобретено гораздо позднее натуральных чисел, в Индии

Это открытие считается одним из величайших событий в математике.

Также нельзя забывать, что рациональные и иррациональные числа хоть и относятся к действительным, но подчиняются разным правилам счета. Это нужно учитывать при решении уравнений и примеров.

Что мы узнали?

Мы поговорили о множествах чисел. Выяснили, что числа делятся на действительные числа и комплексные числа. Действительные числа в свою очередь подразделяются на рациональные и иррациональные. Мы поговорили о разнице в действиях с рациональными и иррациональными числами. Проговорили все подмножества иррациональных чисел.

1. /10

   Вопрос 1 из 10

Числа. Действительные числа.

Понятие действительного числа: действительное число — (вещественное число), всякое неотрицательное или отрицательное число либо нуль. С помощью действительных чисел выражают измерения каждой физической величины.

Вещественное, или действительное число возникло из необходимости измерений геометрической и физической величин мира. Кроме того, для проведения операций извлечения корня, вычисления логарифма, решения алгебраических уравнений и т.д.

Натуральные числа образовались с развитием счета, а рациональные с потребностью управлять частями целого, то вещественные числа (действительные) используются для измерений непрерывных величин. Т.о., расширение запаса чисел, которые рассматриваются, привело к множеству вещественных чисел, которое кроме рациональных чисел состоит из других элементов, называемых иррациональные числа.

Множество действительных чисел (обозначается R) — это множества рациональных и иррациональных чисел собранные вместе.

Действительные числа делят на рациональные и иррациональные .

Множество вещественных чисел обозначают и зачастую называют вещественной или числовой прямой. Вещественные числа состоят из простых объектов: целых и рациональных чисел.

Число, которое возможно записать как отношение, где m — целое число, а n — натуральное число, является рациональным числом .

Всякое рациональное число легко представить как конечную дробь либо бесконечную периодическую десятичную дробь.

Бесконечная десятичная дробь, это десятичная дробь, у которой после запятой есть бесконечное число цифр.

Числа, которые нельзя представить в виде , являются иррациональными числами.

Всякое иррациональное число легко представить как бесконечную непериодическую десятичную дробь.

Рациональные и иррациональные числа создают множество действительных чисел. Всем действительным числам соответствует одна точка координатной прямой, которая называется числовая прямая.

Для числовых множеств используются обозначения:

• N — множество натуральных чисел;
• Z — множество целых чисел;
• Q — множество рациональных чисел;
• R — множество действительных чисел.

Теория бесконечных десятичных дробей.

Вещественное число определяется как бесконечная десятичная дробь, т.е.:

где ± есть один из символов + или −, знак числа,

a — целое положительное число,

Бесконечную десятичную дробь можно объяснить как число, которое на числовой прямой находится между рациональными точками типа:

Сравнение вещественных чисел как бесконечных десятичных дробей происходит поразрядно. Например, предположим даны 2 положительны числа:

Но при этом нудно обратить внимание на то, что число a,a1a2…an(9)=a,a1a2…an+10 −n. Поэтому если запись одного из сравниваемых чисел, начиная с некоторого разряда это периодическая десятичная дробь, у которой в периоде стоит 9, то её нужно заменить на эквивалентную запись, с нулем в периоде

Арифметические операции с бесконечными десятичными дробями это непрерывное продолжение соответствующих операций с рациональными числами. Например, суммой вещественных чисел α и β является вещественное число α+β, которое удовлетворяет таким условиям:

Десятичная запись нецелых чисел

Нецелые числа могут быть представлены в десятичной записи, которая состоит из целой части и десятичной части, разделенных десятичным разделителем.

Запись нецелого числа может иметь следующий формат:

• Целая часть: целое число слева от десятичного разделителя;
• Десятичная часть: десятичное число справа от десятичного разделителя;
• Десятичный разделитель: запятая или точка, которые разделяют целую и десятичную части;
• Знак числа: может быть «+» или «-«, указывает на положительность или отрицательность числа.

Например:

Нецелое число	Десятичная запись
2.5	2 целая часть, 5 десятичная часть
-1.75	-1 целая часть, 75 десятичная часть
0.3	0 целая часть, 3 десятичная часть

Некоторые примеры десятичной записи чисел могут быть:

1. 0.25
2. -3.14
3. 12.6
4. 9.99

Десятичная запись нецелых чисел удобна для точного представления их значения и проведения математических операций.

Итак, десятичная запись нецелых чисел состоит из целой части, десятичной части и десятичного разделителя, который разделяет эти две части. Этот формат позволяет точно представить нецелые числа и использовать их в математических операциях.

Метод математической индукции в доказательстве иррациональных чисел

Чтобы использовать метод математической индукции для доказательства иррациональности числа, обычно применяют следующий шаги:

1. Показать, что утверждение выполняется для базового случая. В контексте иррациональных чисел, это означает показать, что число не может быть представлено в виде дроби с целыми числами в числителе и знаменателе.
2. Предположить, что утверждение выполняется для некоторого натурального числа k. То есть, предполагается, что число имеет иррациональное представление при n = k.
3. Доказать, что утверждение также выполняется для следующего натурального числа k + 1. То есть, показать, что число имеет иррациональное представление при n = k + 1, исходя из предположения об иррациональности при n = k.

С помощью этих шагов можно установить иррациональность числа для всех натуральных чисел и, следовательно, доказать, что число является иррациональным.

Пример доказательства иррациональности числа √2 с использованием метода математической индукции:

1. Базовый случай: При n = 1 число 2 не может быть представлено в виде дроби с целыми числами в числителе и знаменателе, так как его квадратный корень является иррациональным.
2. Предположим, что √2 является иррациональным для некоторого натурального числа k.
3. Докажем, что √2 является иррациональным для n = k + 1. Предположим, что √2 может быть представлено в виде дроби p/q, где p и q — целые числа без общих делителей, включая делители -1 и 1. Тогда:

√2 = p/q

2 = (p/q)²

2q² = p²

Таким образом, p² должно быть четным числом, а значит, p также должно быть четным числом (если p было бы нечетным, то p² было бы нечетным). Пусть p = 2m, где m — некоторое целое число.

2q² = (2m)² = 4m²

q² = 2m²

Таким образом, q² должно быть четным числом, а значит, q также должно быть четным числом.

Из условия «p и q — целые числа без общих делителей, включая делители -1 и 1» следует, что и p, и q должны быть четными числами, тогда q/2 и p/2 также являются целыми числами без общих делителей.

Теперь можно переписать равенство √2 = p/q в следующем виде:

√2 = (p/2) / (q/2)

Это означает, что √2 может быть представлено в виде дроби с целыми числами в числителе и знаменателе, что противоречит исходному условию. Значит, предположение об иррациональности √2 при n = k + 1 верно.

Таким образом, с использованием метода математической индукции можно доказать, что число √2 является иррациональным.

Понятие действительного числа

Определение

Действительные числа — это категории рациональных и иррациональных числовых значений.

Через R обычно выражается множество действительных чисел (их значения).

Рациональные числовые значения. Эту категорию чисел можно выразить, как положительное или отрицательное дробное значение. Еще есть вариант представлять рациональное число в виде нулевого значения.

Множество рациональных данных имеет следующий вид:

\

Иррациональное число. Данные значения невозможно выразить как деление двух и более целых данных. Такие числа представлены и выражаются как бесконечная, не имеющая определенного периода десятичная дробь.

Множество иррациональных чисел.

\

Данное множество, как правило, состоит из определенного множества рациональных чисел. А также, вместе с иррациональными значениями. Характеризуется множество R как область действительных чисел и обозначается

\

Иначе, можно составить и записать множество двух значений действительных чисел: рационального и иррационального.

\

Следовательно, любое рациональное число возможно записать в виде окончательной десятичной дроби или бесконечной периодической дроби.  Иррациональные значения можно выразить бесконечными не имеющими определенного периода десятичными дробями. Учитывая все вышеизложенное определение действительных чисел можно составить и записать иначе.

Определение

Действительные числа — это значения чисел, которые выражаются, как конечная или бесконечная, имеющая вид периодической и непериодической десятичной дроби. Иными словами, их можно назвать, как вещественные.

Сравнение действительных чисел

Множество действительных чисел обозначается буквой R (от латинской страши R — realis — действительный) и включает в себя как рациональные, так и иррациональные значения.

Числа натуральные и нуля являются действительными и рациональными одновременно. Числа целые тоже являются действительными и рациональными. Дробные числа составляют на самом деле бесконечные десятичные разложения и могут быть как рациональными, так и иррациональными.

Рассмотрим приметы рациональных и иррациональных чисел:

Рациональные числа:

• Можно записать в виде десятичной дроби с конечным или периодическим числовым представлением;
• В законах математики есть правила для операций с рациональными числами;
• Результат деления двух рациональных чисел также будет рациональным числом (если делитель не равен нулю);
• Единственное рациональное число, которое нельзя представить в виде десятичной дроби без периодического представления, это иррациональное число π.

Иррациональные числа:

• Можно записать только в виде бесконечного невозможного представления (бесконечные десятичные разложения без периодической структуры);
• Определение иррационального числа состоит в том, что оно не может быть представлено в виде дроби;
• Как результат деления двух рациональных чисел, может быть как рациональным, так и иррациональным числом.

В данном разделе мы рассмотрели сравнение действительных чисел и обозначили различия между рациональными и иррациональными числами.

Естественная форма числа: определение и особенности

Естественная форма числа – это способ представления числа в виде последовательности цифр без каких-либо дополнительных символов или знаков.

В отличие от десятичной или другой позиционной формы, естественная форма числа не содержит позиционных разрядов или знаков операций. Это означает, что порядок и значение цифр в числе не имеют значения, и только сама последовательность цифр определяет число.

Основные особенности естественной формы числа:

• Простота представления. Естественная форма числа состоит только из цифр и не требует специальных символов или знаков. Это делает ее удобной для использования в различных контекстах.
• Гибкость интерпретации. Поскольку в естественной форме числа нет позиционных разрядов или знаков операций, она может быть интерпретирована по-разному в зависимости от контекста и требований.

Например, число «1234567890» в естественной форме может быть интерпретировано как:

• Десять цифр подряд.
• Четыре группы цифр: «12», «34», «56» и «78», с разделением между группами или без него.
• Любая другая комбинация или разбиение групп цифр в соответствии с требованиями контекста.

Таблица ниже представляет примеры чисел в естественной форме:

Число	Естественная форма
1	1
42	42
123456	123456
9876543210	9876543210

Вывод: естественная форма числа предоставляет простой и гибкий способ представления чисел без позиционных разрядов или знаков операций. Она может быть интерпретирована по-разному в различных контекстах и предоставляет удобство в использовании.

Как недействительные числа возникают

Недействительное число – это число, нарушающее математические правила и не может быть представлено в числовой системе. Оно часто возникает из-за ошибок в вычислениях или применении неправильных математических операций.

Одна из наиболее распространенных причин возникновения недействительных чисел – деление на ноль. Эта операция является недопустимой в математике, поскольку немыслимо поделить что-то на ноль. Таким образом, результат такой операции будет недействительным числом.

Применение неправильной математической операции также может привести к недействительным числам. Например, попытка извлечения квадратного корня из отрицательного числа приведет к появлению недействительного числа.

Кроме того, некоторые операции, такие как логарифмирование отрицательного числа, могут привести к появлению недействительного числа. Также в некоторых случаях, когда результат операции не может быть точно представлен в пределах конечного количества десятичных знаков, может возникнуть недействительное число.

Важно помнить, что недействительные числа не имеют физического смысла и не могут быть использованы в научных расчетах, поэтому важно избегать ошибок, которые могут привести к их возникновению

Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Класс и характеристика действительных чисел

Все действительные значения чисел можно представить по следующей классификации:

простое натуральное значение или целое числовое значение — это простые числовые значения, которые возникают при простом и естественном счете. В технических науках множество целых числовых значений принято обозначать символом Z.

Любое значение множества натуральных чисел N — это, значение   подмножеств целых числовых значений, которые обозначаются буквой  Z .

Целым вполне возможно назвать, любое число натурального значения. Однако, целое число не всегда будет является натуральным числом, и это следует всегда помнить.

Натуральные числа, можно определить двумя методами:

значения, которые возникают, при подсчете определенных предметов, которые являются числительными (первый день, четвертый урок, третий ребенок);

обозначение конкретных событий или простых предметов (три слова, пять рулонов).

В первом случае нумерация начинается с единичного значения, а для второго характерен подсчет, с нулевого знака.

положительное и отрицательное дробное значение, любого вида;

Простое положительное число — это как правило число, которое располагается с правой стороны от нулевого значения. Ему присвоен знак плюс, иными словами числа с плюсовым значением.

Например: 1;15;36;12356.  

Рассмотрим значение   15 — целое число со знаком плюс, то есть положительное значение. На координатной прямой оно располагается справа от нулевого значения или точки первоначального отсчета.  

Отрицательное число — это данное определение идентично вышеуказанному положительному, за исключение левой стороны от нулевого значения и знак меняется с плюса на минус.

Примеры целых отрицательных чисел: − 52 ,   − 258 ,   − 1 -528, -2568, -1. Нулевое значение делит между собой  положительные и отрицательные целые числа.  В тоже время оно, является ни положительным и ни отрицательным Числовое значение, которое является обратным каждому отрицательному значению, следовательно, является положительным целым числом.  

Сравнивая с нулевым значением, можно сформулировать и другие определения, конкретно опираясь на ноль.

Например: числа, которые являются меньше нуля, можно назвать отрицательными целыми числовыми значениями.

Числа, которые больше нулевого данного числа, будет называться простыми положительными значениями. Положительные данные, находящиеся правее от нулевого числового значения, следовательно, отрицательные мы увидим слева от нуля. Мы уже рассмотрели и изучили правило, что натуральные числа — это целый ряд или подмножество целых значений. Рассмотрим это подробнее. Несколько данных натуральных чисел объединяют в себя целые положительные значения. Из этого следует, что множество отрицательных целых значений числа, может быть представлено, как множество значений, с обратным значением знака к натуральным числам

 Стоит уделить внимание следующему понятию!

Любое натуральное число значение, может иметь свойство целого значения, однако, не каждое целое значение может быть натуральным. Отвечая на популярный вопрос, можно смело ответить — что являться не могут.

Дадим определения таким значениям неотрицательные и не положительные.

Неотрицательные целые числа — это положительные числа и нулевое числовое значение.

Неположительные целые числа — это отрицательные целые числа и значение равное нулю.

Как мы уже говорили ранее числовое данное равное нулю, не относится ни к какому из изученных натуральных значений. Простыми примерами неотрицательных чисел могут быть следующие значения: 45; 142; 26589;105689.

В свою очередь -52; -5698; -12598 это неположительные значения. Также есть смешанные значения, и дроби десятичного значения, они бывают:

1. положительные;
2. отрицательные;
3. периодические;
4. бесконечные;
5. непериодические.

Выразить действительные числа, можно в следующем виде:

• корни числа;
• степенное значение;
• логарифмическое;
• сумма;
• разность;
• произведение;
• деление.

Применяя все перечисленные свойства числа действительного типа, можно составлять различного вида математические примеры, уравнения, тригонометрические и алгебраические функции. Составим и запишем несколько примеров решения:

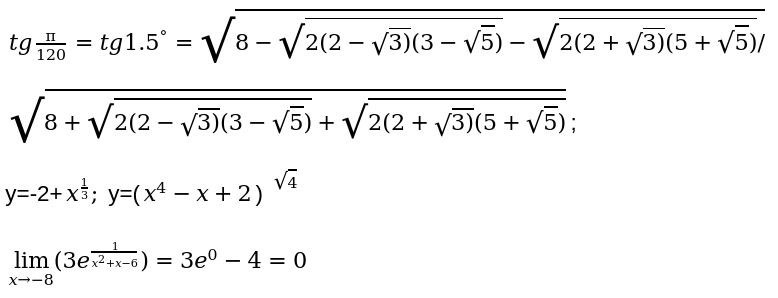
Советы по предотвращению ошибок при вводе чисел

1. Будьте внимательны при вводе чисел

Ошибки ввода часто происходят из-за невнимательности. Поэтому всегда старайтесь быть внимательными при вводе чисел. Проверьте введенные цифры перед нажатием кнопки «Подтвердить» или «Отправить».

2. Используйте контрольные суммы

Популярный способ предотвратить ошибки при вводе чисел — использование контрольных сумм или проверочных цифр. Контрольная сумма — это дополнительный символ, добавляемый в конец числа, который вычисляется на основе других цифр. При получении числа, система автоматически проверяет контрольную сумму и определяет, является ли число действительным.

3. Используйте форматирование чисел

Чтобы сделать ввод чисел более удобным и предотвратить ошибки, используйте форматирование чисел. Например, можно разделять тысячи, миллионы и т.д. запятой или пробелом. Это позволит лучше визуализировать число и упростить ввод.

4. Проводите дополнительные проверки при вводе

Не полагайтесь только на автоматическую проверку введенных чисел. Дополнительно проводите проверку на корректность числа и его соответствие заданным критериям. Например, проверяйте, что число находится в определенном диапазоне или имеет правильное количество цифр.

5. Используйте подсказки и подсветку ошибок

Для предотвращения ошибок можно использовать подсказки и подсветку ошибок при вводе чисел. Например, можно выводить подсказку с правильным форматом числа или выделять красным цветом введенное число, если оно некорректно.

6. Проверьте введенное число перед его сохранением

Прежде чем сохранить введенное число, проведите финальную проверку. Убедитесь, что число действительно является корректным и соответствует требованиям системы или приложения.

7. Обратитесь за помощью

Если у вас возникают сложности с вводом чисел или вы сомневаетесь в правильности введенного числа, не стесняйтесь обратиться за помощью. Обратитесь к администратору системы или к специалисту, который поможет вам решить эту проблему.