Обоснование 26 за­да­ния

Практическое применение невесомости нити

Свойство невесомости нити находит широкое применение в различных областях науки, техники и медицины. Вот несколько примеров:

1. Физика и аэрокосмическая промышленность. Из-за своей невесомости нить может использоваться в качестве упругого элемента для измерения давления, тяжести, силы тяжести и других физических величин. Такие нити могут быть использованы в космических аппаратах, роботах и при проведении экспериментов в невесомости.

2. Медицина. Нить невесома и нерастяжима, что делает ее идеальным материалом для использования в хирургии, в том числе при проведении сложных операций. Такие нити обеспечивают точное и надежное заживление ран, а также уменьшают риск развития инфекций.

3. Технологии. Нить невесома и нерастяжима, что позволяет ее использовать в производстве микросхем, электронных компонентов и оптических устройств. Она используется для создания сверхпроводников, квантовых компьютеров и других высокотехнологичных устройств.

4. Искусство и дизайн. Благодаря своей невесомости и нерастяжимости, нить может быть использована в декоративных целях. Она может использоваться для создания уникальных пространственных композиций, а также для создания легких и изящных одежды и аксессуаров.

Таким образом, свойство невесомости нити открывает широкие возможности для ее практического применения в различных областях. Нити сочетают в себе прочность и легкость, что делает их незаменимыми во многих отраслях науки и промышленности.

Критерии оценивания задания 26 ЕГЭ по физике

Это последнее задание экзамена и одно из самых «дорогих». За верное решение и соответствие всем критериям можно получить 4 первичных балла.

Критерий 1

Первым критерием при проверке задания является верность обоснования возможности использования законов или закономерностей для решения задачи.

Если дать верное обоснование без ошибок и указать на все необходимые элементы, то по этому критерию можно заработать 1 балл. В случае, если обоснования нет, допущена ошибка или приведены не все элементы, выставляется 0 баллов по этому критерию.

Критерий 2

Во втором блоке критериев есть 4 пункта, по каждому из которых будут оценивать ответ.

1. При решении задачи нужно убедиться, что в ответе записаны все положения и законы, которые необходимы для ее решения.
2. При введении новых буквенных значений величин в ответе необходимо давать их описание. Однако, константы, величины из условия задачи и стандартные обозначения величин физических законов могут быть исключением.
3. В ответе должны быть проведены все нужные математические расчеты и преобразования.
4. В конечном ответе нужно записать правильный результат с указанием единиц измерения.

Если все эти пункты присутствуют, описания и решения верны, теория приведена в полном объеме, по этому критерию можно заработать 3 балла.

Силы упругости: пружины, канаты и нити

В задачах в этой статьи рассмотрены случаи, когда тело поднимают или опускают с ускорением. При этом натяжение нити, на которой подвешен груз, разное. Даны примеры составления уравнений по второму закону Ньютона в проекциях на оси.

Задача 1. Грузовик взял на буксир легковой автомобиль массой т и, двигаясь равноускоренно, за с проехал м. На сколько при этом удлиняется трос, соединяющий автомобили, если его жесткость Н/м? Трение не учитывать.

Удлинение троса можно найти, зная силу упругости:

Так как трение учитывать не нужно, то по второму закону Ньютона

Следовательно,

Определим ускорение грузовика:

Окончательно для удлинения троса получаем:

Ответ получен в метрах, можно записать его в мм: 0,64 мм.

Задача 2. На нити, выдерживающей натяжение Н, поднимают груз массой кг из состояния покоя вертикально вверх. Считая движение равноускоренным, найти предельную высоту , на которую можно поднять груз за с так, чтобы нить не оборвалась.

Запишем второй закон Ньютона в проекция на вертикальную ось:

Тогда ускорение равно:

Высота, на которую тело можно поднять с таким ускорением, равна

Ответ: 5 м

Задача 3. Веревка выдерживает груз массой кг при вертикальном подъеме его с некоторым ускорением и груз массой кг при опускании его с таким же по модулю ускорением. Какова максимальная масса груза , который можно поднимать или опускать на этой веревке с постоянной скоростью?

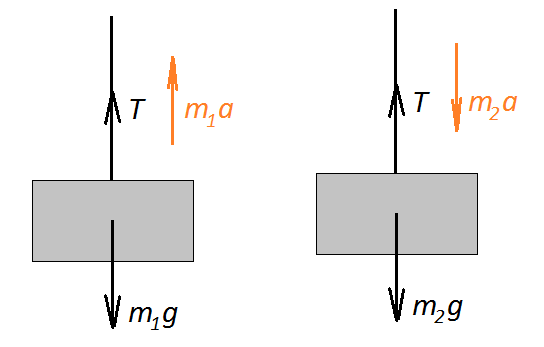
Запишем уравнения по второму закону как для подъема, так и для спуска тела. Направим ось вверх, тогда при подъеме:

При спуске:

Ускорение по условию одно и то же, тогда:

Приравняв, можем найти силу натяжения веревки, которую она выдерживает:

Если бы груз массой просто висел на такой веревке, то мы бы записали

Следовательно,

Ответ: 190 кг

Задача 4. Груз массой кг подвешен к пружине жесткостью Н/м. Длина пружины в нерастянутом состоянии м. Найти длину пружины , когда на ней висит груз. Какой будет длина пружины, если пружина с грузом будет находиться в лифте, движущемся с ускорением м/с, направленным а) вверх; б) вниз?

Если груз повешен на пружину, ее длина увеличивается:

При движении лифта вверх запишем второй закон (ось направлена вверх):

При движении лифта вниз запишем второй закон (ось направлена вверх):

Тогда длина пружины в этом случае:

Ответ: , , .

Задача 5. Четырьмя натянутыми нитями груз закреплен на тележке. Силы натяжения горизонтальных нитей соответственно и , а вертикальных – и . С каким ускорением движется тележка по горизонтальной плоскости?

Запишем уравнения по второму закону в проекциях на оси, которые расположим традиционно: ось вправо, ось – вверх. Тогда, если тележка движется вправо, по оси, имеем:

Из второго уравнения найдем массу груза:

Если же тележка движется влево (против оси), то изменится только первое уравнение:

Тогда ускорение тележки (и груза) равно:

easy-physic.ru

Расчет натяжения троса и реакции опоры

Задача

Однородная балка AB весом P закреплена в точке A шарнирно-неподвижной опорой; трос BC, удерживающий балку, составляет с ней угол α. Определить натяжение троса и реакцию опоры A (рисунок 2.2, а).

Решение

Силы, действующие на балку, приложены к разным ее точкам, поэтому в данной задаче нужно рассмотреть равновесие балки. Балка однородная, поэтому сила P (вес балки) приложена к ее середине (рисунок 2.2, б).

Реакция троса – сила T – направлена вдоль троса. Направление реакции опоры A можно определить, воспользовавшись теоремой о трех силах. По этой теореме линии действия трех непараллельных сил P, T и RA должны пересекаться в одной точке. То есть угол β должен быть равен углу α.

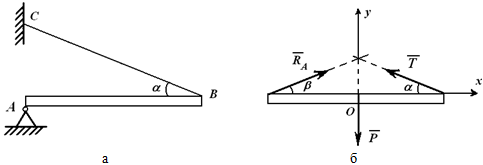
Рисунок 2.2

Так как система находится в равновесии, то

P + T + RA=0. (2.7)

Строим это геометрическое равенство (рисунок 2.3), начиная с известной силы P; под углом α к горизонтали через конец векторa P проводим линию MN, вдоль которой направлена сила T. Так как сумма всех сил должна быть равна нулю, то вектор RA должен заканчиваться в начале вектора P под углом β к горизонту (линия KL).

Рисунок 2.3

Точка пересечения линий MN и KL – это конец вектора T и начало вектора RA. Далее можно определить величины T и RA, умножив длины отрезков на выбранный масштаб или воспользовавшись теоремой синусов:

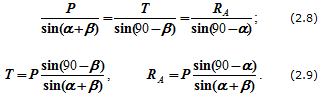
Аналитическое решение предполагает составление двух уравнений. Проецируем векторное равенство (2.7) на выбранные оси координат (рисунок 2.2,б) и получаем два уравнения равновесия с двумя неизвестными:

∑xi=0, -Tcosα+RAcosβ=0;∑yi=0, -P+Tsinα+RAsinβ. (2.10)

Из этих уравнений определяются величины T и RA:

Другие примеры решения задач >>

isopromat.ru

Значение невесомости и нерастяжимости нити в науке

Нить, обладающая свойствами невесомости и нерастяжимости, играет важную роль в многих научных областях. Её уникальные свойства стали основой для разработки и проведения различных экспериментов и исследований.

В физике, невесомая нить используется для создания моделей и демонстраций физических явлений. Например, она может быть использована для изучения механики системы под действием гравитационных сил или для создания маятников и колебательных систем. Невесомая нить позволяет исключить влияние силы тяжести и сосредоточиться исключительно на изучении других физических особенностей системы.

В микробиологии и биохимии невесомость и нерастяжимость нити играют важную роль при проведении опытов и анализе различных образцов. Она может использоваться для изоляции отдельных клеток или генов, для создания мембран и фильтров, для манипулирования жидкостями и реагентами. Нити с указанными свойствами позволяют контролировать и управлять микроскопическими объектами, что открывает широкие возможности для исследования и разработки новых методов и технологий.

Кроме того, невесомая и нерастяжимая нить нашла применение в аэронавтике и космических исследованиях. В условиях невесомости, она может использоваться для крепления и фиксации различных элементов и оборудования на борту космических аппаратов. Недеформируемость нити позволяет обеспечить надежность и стабильность фиксации, что является важным требованием при проведении экспериментов в космосе.

Итак, свойства невесомости и нерастяжимости нити не только удивительны с точки зрения физических законов, но и находят широкое применение в науке. Они позволяют расширить возможности исследования и анализа, а также разрабатывать новые методы и технологии, которые приводят к новым открытиям и достижениям в различных областях науки.

Области применения невесомой нерастяжимой нити

Невесомая нерастяжимая нить имеет широкий спектр применения и может быть использована в различных областях. Ниже перечислены некоторые из них:

• Медицина: невесомая нить используется в хирургии для проведения сложных операций, например, при сшивании ран или вмятин.
• Космическая отрасль: нить используется в астронавтике для создания структур, удерживающих различное оборудование в невесомости.
• Искусство: художники используют невесомую нить для создания уникальных инсталляций или скульптур.
• Спорт: нить применяется в некоторых виде спорта, например, в воздушной гимнастике, где она помогает атлетам выполнять сложные трюки.
• Строительство: невесомая нерастяжимая нить используется в строительных работах для отметки горизонтальных и вертикальных линий.
• Физика и наука: нить применяется в экспериментах и исследованиях для измерения различных физических величин.

Это лишь некоторые из областей применения невесомой нерастяжимой нити. Ее уникальные свойства делают ее ценным инструментом в различных сферах деятельности.

Ограничения нерастяжимой нити

Однако, при использовании нерастяжимой нити необходимо учитывать определенные ограничения:

1. Отсутствие силы сопротивления: В реальности нити могут иметь небольшую упругость и сопротивление растяжению. Однако, в модели нерастяжимой нити рассматривается идеализированная ситуация, в которой сила сопротивления отсутствует.
2. Отсутствие веса нити: В модели нерастяжимой нити также не учитывается вес самой нити. Это означает, что нить считается абсолютно легкой и не оказывает влияния на исследуемую систему.
3. Отсутствие трения: В реальных условиях нить может претерпевать трение при контакте с другими объектами. Однако, в идеализированной модели нерастяжимой нити предполагается, что нить не притягивается кракту или другим объектам, и трения нет.
4. Соблюдение закона сохранения энергии: При использовании модели нерастяжимой нити необходимо учитывать закон сохранения энергии, так как нить не поглощает и не отдает энергию в процессе движения.

Использование модели нерастяжимой нити позволяет значительно упростить решение задач и анализ системы. Однако, необходимо учитывать эти ограничения и быть осторожными при интерпретации результатов.

Значение нерастяжимости нити в промышленности

Одной из основных причин, по которой нерастяжимость нити является такой востребованной характеристикой, является сохранение структуры и формы материала на протяжении всего процесса производства и использования. Если нить имеет возможность растягиваться, это может привести к искажению формы изделия, потере прочности и сохраняемым характеристикам. Нерастяжимость нити позволяет обеспечить стабильность и качество материала.

В текстильной промышленности нерастяжимость нити особенно важна при производстве тканей, швейных изделий и синтетических материалов. Она позволяет избежать деформаций и уплотнений в материале, обеспечивает точность размеров и снижает возможность повреждений при дальнейшей обработке.

В медицинской и спортивной промышленности нерастяжимая нить используется в создании швов и стежков, которые должны быть прочными и долговечными. Нерастяжимость нити обеспечивает сохранение шва и стежка в идеальном состоянии при любых нагрузках и растяжениях, что является особенно важным в контексте медицинских операций и спортивных тренировок.

В авиации и аэрокосмической промышленности нерастяжимость нити играет решающую роль в безопасности и надежности компонентов и конструкций. Она позволяет изготавливать сильные и стойкие соединения, которые способны выдерживать большие нагрузки и экстремальные условия, такие как высокие температуры и давления. Нити с высокой нерастяжимостью используются для создания швов, арматуры и крепежных элементов.

Таким образом, значение нерастяжимости нити в промышленности заключается в обеспечении стабильности и прочности материала, сохранении формы и размеров изделия, а также в создании надежных соединений и компонентов. Это свойство играет важную роль в различных отраслях и способствует повышению качества и надежности производимых изделий.

Нить, будучи невесомой и нерастяжимой, обладает рядом значимых свойств и применений.

Во-первых, невесомость нити означает, что она может быть использована для создания легких и деликатных конструкций. Например, нить может служить основой для вышивки, создания воздушных штор или вязания тонкой одежды. Благодаря своей невесомости, нить с легкостью принимает форму и позволяет создавать эстетически привлекательные изделия.

Во-вторых, нерастяжимость нити имеет важное значение для его применения в различных сферах. Нить, не поддаваясь растяжению, является надежным материалом для шитья и вязания, поскольку удерживает свою форму и не теряет прочность со временем

Кроме того, нерастяжимая нить может использоваться в медицинских процедурах, где требуется выдерживать натяжение и не допускать отклонений.

Таким образом, невесомость и нерастяжимость нити способствуют ее широкому применению в различных областях, от ремесел и дизайна до медицины и строительства. Эти свойства делают нить универсальным и важным материалом, способным создавать красоту, облегчать процессы и обеспечивать надежность.

Самые популярные законы физики, которые могут встретиться в задаче

Самый большой раздел, представленный в кодификаторе, — механика. Задачи на темы именно из этого раздела встречаются в задании 26. Приведем некоторые из законов с указанием функции для обоснования.

Законы Ньютона	Материальная точка	Размеры тел не существенны в решении
Инерциальная система отсчёта	Можно пренебречь влиянием вращения Земли
Движение связанных тел	Невесомая нить	— Массой нити можно пренебречь по сравнению с массой связанных ею тел — Силы натяжения одинаковы во всех точках нити
Нерастяжимая нить	Деформацией нити в условиях данной задачи можно пренебречь
Идеальный блок	Массой блока и силой трения в условиях данной задачи можно пренебречь
Закон Гука		Тело восстанавливает свою форму после снятия деформирующей силы

Расчет натяжения каната.

Исходные данные

Рис 1. Расчетная схема механизма.

1-Грузоподьемность Q=2 тонны

2-Высота подъема груза H=3,5 м

3-Скорость подъема Vп=18 м/мин

4-Кратность полиспаты =1

5-Количество ветвей набегающих на барабан а=1

6-Режим работы- средний

Выбор типа подъемного органа.

В качестве подъемного органа выбираем стальной проволочный канат двойной свивки.

Рис.2 Поперечное сечение каната.

Расчет натяжения каната.

Максимальное натяжение на ветке каната.

Fmax=Qg=2000*9.81=19620 H

Расчетное разрывное усилие каната.

Fрасч=k* Fmax=19620*5=98100 H

k-для среднего режима работы коэффициент запаса равен 5.

По ГОСТ 2688-80 выбираем канат двойной свивки по Fрасч.

Канат 14-Г-I-1578 где,

· Первая цифра 14- диаметр каната, мм.

· Вторая Г- канат грузовой.

· Третья I- марка проволоки.

· Четвертая 1578- максимальное разрывное усилие, Н

Конструкция каната

Канат ЛК-Р-6х19(1+6+6/6)+1.о.с ГОСТ 2588-80 ,где

ЛК-Р- с линейным касанием проволок разных диаметров в верхнем слое пряди.

· 6х19- канат шестипрядный по 19 проволок в пряди.

· (1+6+6/6)- навивка проволок по слоям.

· 1.о.с.- органический сердечник.

Расчет барабана.

Рис.3 Профиль канавок на барабане

mykonspekts.ru

Современная теория механизмов

Существует понятие «типовые механизмы», которое объединяет ряд простых механизмов, имеющих при различном функциональном назначении применение в разнопрофильных машинах. К ним относятся простейшие механизмы:

• рычажные;
• зубчатые;
• планетарные;
• кулачковые;
• манипуляционные и т.п.

Рациональное проектирование машин определяется вариантами используемых в их составе простых механизмов и систем механизмов, благодаря которым изыскиваются оптимальные технические решения.

Существует две системы классификации простых механизмов: по назначению и конструкции. На практике их применение часто основывается на взаимно сочетающихся характеристиках.

Теория механизмов предполагает опираться на те свойства простых механизмов, которые являются общими, независимо от конкретного целевого назначения аппарата. К примеру, механизм в виде зубчатого колеса, создающий вращательное движение, используется как в часах, так и в автомобиле, промышленных станках и т.д.

Насколько эффективной будет работа создаваемой машины, зависит от правильности выбора механизмов. Выбор происходит в пользу тех, у которых выше производительность, надежность, точность. Также акцент делается на экономичность и доступность сырья для изготовления.

Применение механизмов началось в древности. Первыми из них были ловушки для зверей, которые удовлетворяли основной инстинкт человека — борьбу с голодом.

Сегодня для современной техники большое значение имеют:

1. Механизмы манипуляторов (устройств, предназначенных для воспроизведения движений руки человека). Благодаря таким устройствам создаются промышленные роботы, которые приходят на помощь в самых сложных условиях и быстро выполняют утомительные работы, часто во вредных условиях.
2. Самонастраивающиеся механизмы. Особенностью конструкции является способность изменять автоматически свое движение, создавая оптимальные условия для общей работы прибора.
3. Механизмы медицинских аппаратов. Они воспроизводят физиологические процессы в теле человека. Примеры: искусственные легкие, искусственная почка, стимулятор сердца и т.п. Благодаря использованию таких приборов удается сохранить человеку жизнь даже в критических ситуациях.

Еще недавно в создании технических приборов использовались только простые механизмы, которые имели одну либо две степени подвижности. Сегодня их в одном приборе заключается много, что стало приемлемым благодаря использованию высокотехнологичных систем управления. Они в состоянии обеспечить эффективное функционирование аппаратов целиком или их отдельных частей.

2.3. Свободные колебания. Математический маятник window.top.document.title = «2.3. Свободные колебания. Математический маятник»;

Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести F_τ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Рисунок 2.3.1.Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге

Если обозначить через x линейное смещение маятника от положения равновесия по дуге окружности радиуса l, то его угловое смещение будет равно φ = x / l. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x, а

Только в случае малых колебаний, когда приближенно можно заменить на математический маятник является гармоническим осциллятором, т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15–20°; при этом величина отличается от не более чем на 2 %. Колебания маятника при больших амплитудах не являются гармоническими.

Для малых колебаний математического маятника второй закон Ньютона записывается в виде

Таким образом, тангенциальное ускорение a_τ маятника пропорционально его смещению x, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

Эта формула выражает собственную частоту малых колебаний математического маятника.

Следовательно,

Модель. Математический маятник

Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

Здесь d – расстояние между осью вращения и центром масс C.

Рисунок 2.3.2.Физический маятник

Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ. Это означает, что только при малых углах φ, когда sin φ ≈ φ, физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний

см. §1.23

εIO

Здесь ω – собственная частота малых колебаний физического маятника.

Следовательно,

Более строгий вывод формул для ω и T можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение ε есть вторая производная углового смещения φ по времени:

Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде

Это уравнение свободных гармонических колебаний (). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.

По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции I можно выразить через момент инерции I_C относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:

Окончательно для круговой частоты ω свободных колебаний физического маятника получается выражение:

клеймо для выжигания по дереву

znakmastera.ru

Примеры применения легкой нерастяжимой нити в различных отраслях

Легкая нерастяжимая нить — это уникальный материал, который находит применение во многих отраслях. Ее свойства позволяют использовать ее в различных сферах деятельности, от медицины до строительства. Ниже приведены несколько примеров использования такой нити.

1. Медицина

В медицинской сфере легкая нерастяжимая нить используется в хирургии для проведения различных операций. Она может использоваться для шитья ран, замещения сосудов, а также для создания швов на внутренних органах. Благодаря своей прочности и долговечности, такая нить является незаменимым инструментом для хирургов.

2. Текстильная промышленность

В текстильной промышленности легкая нерастяжимая нить используется для создания прочных и долговечных швов на текстильных изделиях. Она позволяет увеличить срок службы изделий и предотвратить их разрушение при нагрузках. Такая нить может использоваться при пошиве одежды, обуви, сумок и других текстильных изделий.

3. Авиационная промышленность

В авиационной промышленности легкая нерастяжимая нить используется для создания швов на парашютах, авиационных тросах и других компонентах. Ее нерастяжимость и прочность позволяют обеспечить безопасность и надежность авиационных конструкций.

4. Спорт

В спортивной индустрии легкая нерастяжимая нить используется для создания спортивных снарядов, таких как мячи, сетки и др. Она позволяет увеличить прочность и долговечность спортивного снаряжения, что обеспечивает безопасность при его использовании.

5. Строительство

В строительной сфере легкая нерастяжимая нить может использоваться для создания каркасов и фиксации различных элементов конструкции. Она обладает высокой прочностью и устойчивостью к различным нагрузкам, что делает ее отличным материалом для укрепления и фиксации различных компонентов здания или сооружения.

Примеры применения легкой нерастяжимой нити в различных отраслях:
Отрасль
Применение нити

Медицина
Шитье ран, замещение сосудов, создание швов на внутренних органах

Текстильная промышленность
Создание прочных и долговечных швов на текстильных изделиях

Авиационная промышленность
Создание швов на парашютах, авиационных тросах и других компонентах

Спорт
Создание спортивных снарядов (мячи, сетки и др.)

Строительство
Создание каркасов и фиксация элементов конструкции

Легкая нерастяжимая нить является универсальным материалом, который может быть использован в различных отраслях и сферах деятельности. Ее прочность и нерастяжимость делают ее незаменимым инструментом для создания прочных и долговечных конструкций, изделий и решений.