Графики функций и их отношения
В математике график функции – это подмножество декартовой плоскости, на котором точки (x, y) удовлетворяют условию y = f(x), где f – данная функция. График функции может быть линейным, криволинейным или состоять из нескольких кусочно-линейных отрезков.
Отношение двух графиков функций может быть определено по типу их пересечения. Например, если две функции не имеют общих точек или имеют только одну, они называются несвязанными или касающимися. Если же функции пересекаются в нескольких точках, то они являются соответственно пересекающимися или имеющими точки касания.
Одним из способов определения отношений графиков является анализ их наклонов. Наклон графика функции возрастает, когда функция возрастает, и убывает, когда функция убывает. Поэтому, если две функции имеют одинаковый наклон, они могут быть классифицированы как параллельные.
Также отношение графиков функций может быть определено по их взаимной позиции. Например, если график одной функции находится над графиком другой функции на всем интервале их пересечения, то эти функции называются неравномерными. Если же графики лежат с одной стороны от оси x или y, то функции называются монотонными.
- Таким образом, графики функций могут иметь различные отношения в зависимости от типов их пересечения, наклонов и взаимной позиции.
- Анализ отношений графиков функций может помочь понять, как они связаны между собой и в каких случаях они могут быть использованы в рамках математических проблем и задач.
Операции над отношениями
В математике, отношение между элементами двух множеств представляет собой способ установления связи или соответствия между этими элементами. Операции над отношениями позволяют строить новые отношения на основе уже существующих. Рассмотрим основные операции:
- Объединение (сумма) отношений:
- Объединение двух отношений A и B обозначается как A ∪ B.
- Объединением двух отношений является такое отношение, в которое входят все элементы из обоих отношений.
Пересечение отношений:
- Пересечение двух отношений A и B обозначается как A ∩ B.
- Пересечением двух отношений является такое отношение, в которое входят только элементы, принадлежащие и A, и B.
Разность отношений:
- Разностью двух отношений A и B обозначается как A \ B.
- Разностью двух отношений является такое отношение, в которое входят только элементы, принадлежащие A, но не принадлежащие B.
Декартово произведение отношений:
- Декартово произведение двух отношений A и B обозначается как A × B.
- Декартово произведение отношений представляет собой множество всех упорядоченных пар (a, b), где a принадлежит A, а b принадлежит B.
Эти операции позволяют строить новые отношения, комбинируя элементы из исходных отношений и соблюдая определенные правила. Они широко используются в различных областях математики, программирования и других научных дисциплинах.
Отношение толерантности
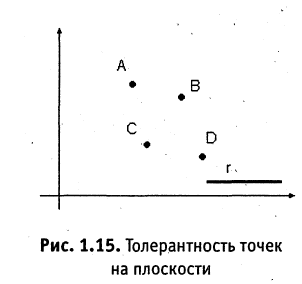
Отношение заданное на множестве М, называется отношением толерантности, если оно рефлексивно, симметрично и нетранзитивно. Обозначение: Если потребовать транзитивность всех пар элементов из М, то получим эквивалентное отношение. Следовательно, толерантность может рассматриваться как расширение эквивалентности. Эквивалентность — в смысле равенства, толерантность — в смысле сходства, похожести. Содержательно толерантность означает следующее: объект находится в данном отношении сам с собой (рефлексивность), сходство двух объектов не зависит от порядка сравнения (симметричность), но если первый объект сходен со вторым, а второй сходен с третьим, то не обязательно, что первый был сходен с третьим. Толерантность позволяет третьим, то не обязательно, что первый был сходен с третьим. Толерантность позволяет формализовать интуитивные представление о сходстве объектов, их похожести в чем-то. Например, отношение «быть на расстоянии не более r», заданное на множестве точек на плоскости. Рис. 1.15 иллюстрирует этот пример. Точка А отстоит от В и С не более чем на r, так же как точка В от Д и С в то время как А находится от Д на расстоянии, значительно большем, чем r.
Величины и их измерение
Когда мы измеряем какую-либо величину, мы пытаемся привести ее к определенной единице измерения. Например, когда мы измеряем длину, мы используем метры или сантиметры в качестве единиц измерения. Это позволяет нам сравнивать и оценивать разные объекты и предметы на основе их размеров.
Но как мы можем быть уверены, что наши измерения точны и надежны? Важно использовать правильные инструменты измерения и следовать определенным правилам. Например, при измерении длины, мы должны приставлять начало измерения к одному концу объекта и четко указывать конечную точку
Также, необходимо выбирать подходящую единицу измерения, чтобы избежать чрезмерно больших или маленьких чисел.
Давайте рассмотрим пример, чтобы все стало более понятным. Представьте, что вам нужно измерить длину стола. Вы берете свою линейку и начинаете измерять. Вы находите, что длина стола составляет 1 метр и 50 сантиметров. Используя правильные единицы измерения и точные инструменты вы получаете точный результат, который можно сравнить с другими объектами и предметами.
Важно знать также, что величины могут быть разными — скалярными и векторными. Скалярные величины имеют только численное значение, такие как масса или время
Векторные величины имеют не только численное значение, но и направление, такие как сила или скорость.
Изучение величин и их измерение помогает нам лучше понять и описать мир вокруг нас. Математика предоставляет нам инструменты для измерения и работы с различными величинами, позволяя нам решать задачи и находить решения в реальной жизни.
Свойства и операции с знаками отношения
Знаки отношения в математике обладают несколькими основными свойствами, которые позволяют выполнять различные операции с ними:
- Симметричность: Если два объекта связаны отношением, то порядок объектов не важен. Например, если A больше B, то B меньше A.
- Транзитивность: Если объект A связан с объектом B и объект B связан с объектом C, то объект A также связан с объектом C. Например, если A больше B и B больше C, то A также больше C.
- Рефлексивность: Каждый объект связан с самим собой. Например, каждое число больше или равно самому себе.
С использованием знаков отношения можно выполнять следующие операции:
- Сравнение: Сравнивать два объекта и устанавливать, является ли отношение между ними истинным или ложным. Например, можно сравнивать числа и устанавливать, является ли одно число больше, меньше или равно другому.
- Упорядочение: Отношение «больше» или «меньше» позволяет упорядочивать объекты. Например, можно упорядочивать числа, так что каждое следующее число больше предыдущего.
- Композиция: Комбинировать знаки отношения, чтобы получить новые отношения. Например, можно скомпоновать отношения «больше» и «меньше» для получения отношения «не равно».
Отношение простых дробей
Отношение простых дробей — это взаимосвязь между двумя или более дробями, выраженная с помощью математического символа отношения «:». Отношение дробей позволяет сравнивать и сопоставлять дроби между собой на основе их числовых значений.
Простые дроби — это дроби, в которых числитель и знаменатель являются натуральными числами и не имеют общих делителей, кроме единицы (дроби, которые не могут быть упрощены). Чтобы выразить отношение двух или более простых дробей, можно использовать следующие правила:
- Если знаменатели дробей одинаковы, отношение определяется по числителям. Дробь с большим числителем будет иметь большее значение.
- Если знаменатели дробей разные, для сравнения дробей необходимо привести их к общему знаменателю. После этого отношение определяется по числителям, как в первом правиле.
- Если числители дробей одинаковы, отношение определяется по знаменателям. Дробь с меньшим знаменателем будет иметь большее значение.
- При необходимости можно упростить дроби, чтобы сравнить их отношение. Для этого нужно найти их наибольший общий делитель и поделить числитель и знаменатель на него.
Например, рассмотрим отношение двух простых дробей — 1/3 и 2/5. Чтобы сравнить их, приведем их к общему знаменателю, который составляет 15. Получим следующие дроби: 5/15 и 6/15. Теперь сравним их по числителям и увидим, что 6/15 больше, чем 5/15. Следовательно, отношение 2/5 больше, чем 1/3.
Отношение простых дробей позволяет сравнивать и ранжировать дроби в соответствии с их значениями
Это важное понятие, которое используется в различных областях математики и естественных наук
Отношение и часть от числа
Посмотрим, какие еще можно сделать выводы, зная отношение.
Мы знаем, что, чтобы найти часть от числа (другими словами, дробь от числа), надо умножить число на эту дробь.
Так мы получим число, которое будет частью исходного.
Допустим, изначально у нас было число 4, и мы решили найти от него \(\mathbf>\)
Перемножив, мы получим:
А теперь найдите отношение полученного числа к изначальному.
Для этого разделите одно на другое:
То, что вы получили отношение, равное той дроби, которую мы находили, не совпадение.
Действительно, находя дробь от числа мы получаем число, чье отношение к исходному будет равно этой дроби.
Сформулируем еще более коротко и четко: отношение числа a к числу b обратно дроби, которую нужно взять от числа а, чтобы получить число b.
Пример 1
Известно, что некая дробь от числа 10 равна \(\mathbf>\)
Найдем, какая именно это дробь.
Решение:
Дробь от числа равна отношению полученного числа к изначальному.
Теперь разделим одно на другое и получим ответ.
Ответ: дробь, взяв которую от 10 получили \(\mathbf>\), равняется \(\mathbf>\)
Пример 2
Отношение первого числа ко второму равно \(\mathbf>\), также известно, что первое число равно 6.
Найдем второе число.
Решение:
Мы знаем, что отношение обратно дроби.
Найдем обратное число к \(\mathbf>\)
Теперь можно найти второе число, домножим первое на эту дробь:
Второе число равно 5
Проверка:
Найдем отношение первого числа ко второму, то есть 6 к 5
Получилось то же отношение, что и в условии.
Пример 3
Решим похожую задачу:
Отношение числа а к числу b равно \(\mathbf>\)
Известно, что число b равняется 8-ми, надо найти число а.
Решение:
Найдем, какую дробь число b составляет от числа a, то есть найдем обратное число от отношения:
Теперь, чтобы найти число по его дроби, надо разделить часть от числа на эту дробь.
В нашем случае на дробь надо делить число b :
Ответ: число a равняется 12
Пройти тест и получить оценку можно после входа или регистрации
Отношение величин в математике 6 класс

В математике мы часто сравниваем величины, например, ищем большую или меньшую величину, вычисляем разницу между двумя величинами и т. д. Для этого используются различные отношения величин.
Отношение больше, меньше и равно

Отношение «больше» (>) устанавливается между двумя величинами, когда первая величина больше второй. Например, 5 > 3, это означает, что число 5 больше числа 3.
Отношение «меньше» () устанавливается между двумя величинами, когда первая величина меньше второй. Например, 2
Отношение «равно» (=) устанавливается между двумя величинами, когда они равны. Например, 4 + 1 = 5, это означает, что сумма чисел 4 и 1 равна числу 5.
Отношение больше или равно, меньше или равно
Отношение «больше или равно» (≥) устанавливается между двумя величинами, когда первая величина больше или равна второй. Например, 3 ≥ 2, это означает, что число 3 больше или равно числу 2.
Отношение «меньше или равно» (≤) устанавливается между двумя величинами, когда первая величина меньше или равна второй. Например, 2 ≤ 3, это означает, что число 2 меньше или равно числу 3.
Отношение между числами
Мы также можем сравнивать числа на прямую, с помощью отношений:
- 10 больше 5
- 4 меньше 9
- 7 больше или равно 7
- 3 меньше или равно 3
Отношение с помощью таблицы
Отношения величин можно также представить с помощью таблицы:
| Отношение | Знак | Пример |
|---|---|---|
| Больше | > | 8 > 3 |
| Меньше | 2 | |
| Равно | = | 4 + 1 = 5 |
| Больше или равно | ≥ | 3 ≥ 2 |
| Меньше или равно | ≤ | 2 ≤ 3 |
Все эти отношения помогают нам лучше понять, как величины связаны друг с другом в математике.
Пропорция
Заметив, что отношение килограмма к грамму равно 1000 и что отношение километра к метру также равно 1000, мы можем написать равенство:
или килограмм : грамм = километр : метр, что читается так: отношение килограмма к грамму равно отношению километра к метру; или так: килограмм относится к грамму так, как километр относится к метру (или еще так: килограмм больше грамма во столько раз, во сколько раз километр больше метра).
Равенство двух отношений принято называть пропорцией. Конечно, величины, входящие в каждое отношение, должны быть однородны; так, в нашем примере величины первого отношения — веса, а величины второго отношения — длины.
Из четырех величин, составляющих пропорцию, первая и четвертая называются крайними членами, вторая и третья — средними членами, первая и третья — предыдущими, вторая и четвертая — последующими. Последняя величина называется также четвертой пропорциональной к первым трем величинам.
Мы будем предполагать, что все четыре члена пропорции выражены числами; такую пропорцию мы будем называть числовой.
Равенство отношений: общая информация
Равенство двух отношений в математике означает, что все элементы первого отношения также принадлежат второму отношению, и наоборот. Другими словами, два отношения считаются равными, если они содержат одни и те же элементы.
Чтобы проверить равенство двух отношений, необходимо сравнить все их элементы. Если каждый элемент из первого отношения присутствует во втором отношении, и наоборот, то отношения считаются равными.
Примером равенства двух отношений может служить отношение «быть братьями» и отношение «быть сестрами». Если все братья также являются сестрами, и наоборот, то можно сказать, что отношения «быть братьями» и «быть сестрами» равны.
| Отношение «быть братьями» | Отношение «быть сестрами» |
|---|---|
| Андрей | Алина |
| Иван | Виктория |
| Петр | Анна |
Отношение между величинами
В математике мы часто сталкиваемся с понятием отношения между величинами. Но что это такое и как оно применяется в нашей жизни? Давайте разберемся!
Отношение между величинами — это способ сравнения и связи одной величины с другой. Мы можем сравнивать величины по их значениям и устанавливать между ними различные отношения, такие как «больше», «меньше» или «равно».
Например, представьте, что у вас есть две коробки с яблоками. В первой коробке 10 яблок, а во второй — 5 яблок. Мы можем сказать, что первая коробка содержит в два раза больше яблок, чем вторая. Или мы можем сказать, что отношение числа яблок в первой и второй коробках равно 2:1. Здесь мы применяем понятие отношения между величинами для сравнения количества яблок в двух коробках.
Отношение между величинами может быть выражено не только числами, но и словами. Например, мы можем сказать, что температура воздуха сегодня «холодная» или «теплая» по сравнению с другими днями. В этом случае мы используем отношение между величинами для описания разницы в температуре.
Отношение между величинами также может быть представлено в виде графика или таблицы. Например, при изучении зависимости между количеством потребляемого сахара и уровнем сахара в крови у человека, мы можем построить график, показывающий, как изменяется уровень сахара в зависимости от количества потребленного сахара.
Знание и понимание отношений между величинами важно не только в математике, но и во многих других областях нашей жизни. Например, в экономике мы можем анализировать зависимость между ценой товара и его обьемом продаж, чтобы прогнозировать будущие доходы
В физике и инженерии мы можем использовать отношение между физическими величинами для проектирования и изучения различных систем и механизмов.
Таким образом, отношение между величинами является важным инструментом для сравнения и анализа различных показателей и данных. Оно помогает нам лучше понимать и объяснять мир вокруг нас. Используйте это знание в своей повседневной жизни, чтобы принимать осознанные решения и быть успешным!
Формальное определение соответствия
-
Отображение f: A → B, где каждому элементу a из множества A соответствует ровно один элемент f(a) из множества B.
-
Отображение g: B → A, где каждому элементу b из множества B соответствует ровно один элемент g(b) из множества A.
Если для каждого элемента a из A существует такой элемент b из B, что f(a) = b, и для каждого элемента b из B существует такой элемент a из A, что g(b) = a, то отображения f и g называются взаимнообратными.
Такое соответствие называется взаимнооднозначным, так как каждому элементу одного множества соответствует ровно один элемент другого множества. Это свойство позволяет установить однозначное соответствие между элементами множеств A и B.
Множество и взаимно однозначное соответствие
В математике понятие соответствия играет ключевую роль при определении отношений между элементами множеств. Под соответствием понимается связь между элементами двух множеств, где каждому элементу одного множества сопоставляется элемент другого множества.
Множество, для которого определено соответствие, называется исходным, а множество, на которое происходит отображение, — образом. В случае взаимно однозначного соответствия каждому элементу исходного множества соответствует ровно один элемент образа, и наоборот, каждому элементу образа соответствует ровно один элемент исходного множества.
Взаимно однозначное соответствие является важным и полезным понятием в различных областях математики и ее приложениях. Оно позволяет строить отображения, которые взаимно однозначно связывают элементы множеств, что позволяет формулировать и решать различные задачи и уравнения.
Пример: Рассмотрим множество натуральных чисел N и множество целых чисел Z. Между этими множествами существует взаимно однозначное соответствие, так как каждому натуральному числу можно сопоставить целое число и наоборот.
Взаимно однозначное соответствие определяет биекцию между множествами, которая является важным инструментом для решения различных задач и доказательств в математике.
Для введения и освоения понятия взаимно однозначного соответствия следует углубиться в изучение теории множеств и математической логики.
Соответствие на плоскости
Соответствие на плоскости может быть определено с помощью формулы или алгоритма, который связывает координаты точек на одной плоскости с координатами точек на другой плоскости. Часто используется понятие линейного соответствия, при котором формула или алгоритм представляют собой уравнение прямой.
Примером соответствия на плоскости может быть отображение, при котором каждой точке на плоскости А соответствует точка на плоскости В, причем расстояние между ними сохраняется. Такое соответствие может быть использовано, например, при построении карты или навигационных систем.
Важно отметить, что соответствие на плоскости обладает некоторыми свойствами, такими как сохранение расстояния, углов и ориентации. Эти свойства позволяют использовать соответствия на плоскости для решения различных задач в математике, физике и других науках
Переход от отношений к алгебре
Отношения возникают в математике при обсуждении свойств объективных явлений и их взаимодействий. Часто отношения описываются с помощью таблицы, которая называется матрицей отношений. Все значимые характеристики такой матрицы, например, число строк, столбцов и т. д., детерминируются свойствами отношения.
Алгебра — это часть математики, в которой изучаются операции, применяемые к числам, буквам и другим математическим объектам. В алгебре мы знакомимся с такими понятиями, как переменные, уравнения и полиномы. В ней также используются несколько разных типов отношений, которые могут быть применены к математическим объектам.
Переход от отношений к алгебре обычно происходит при разработке математических моделей. Для того, чтобы использовать отношения при решении сложных задач, часто требуется изменить их форму или представление. Например, мы можем заменить матрицу отношений на формулу, отражающую свойства этого отношения.
В алгебре отношения обычно задаются через символы, которые представляют собой значения, принимаемые переменной в уравнении. Это позволяет более точно определить связь между объектами в модели. Также при использовании алгебры мы можем решать уравнения и находить значения переменных, которые удовлетворяют некоторым условиям, что значительно облегчает решение задач.
Интересная информация

Сегодня вы узнаете о математических фокусах!
Их идея в том, что можно запутать людей математическими преобразованиями, которые выдадут то, что нужно нам.
Фокус 1
Попросите зрителя загадать число и никому не говорить.
Теперь попросите его умножить это число на 2, прибавить к результату 8, разделить на 2 и вычесть задуманное число.
Теперь вы можете уверенно сказать, что у зрителя получилось число 4.
Так получается за счет того, что в процессе преобразований исходное число вообще уходит из цепочки вычислений и остается только четверка.
Попробуй доказать это на формулах, взяв за задуманное число Х
Фокус 2
В нем вы можете угадать День рождения человека.
Попросите зрителя умножить на 2 число дня его рождения, затем пусть он прибавит к результату 5 и умножит это все на 50, после этого попросите зрителя прибавить к этому числу номер месяца рождения (январь- 1, февраль- 2 и т. д.).
Для того чтобы сказать по полученному числу День рождения человека, надо вычесть из числа, названного зрителем, 250 — получится трехзначное или четырехзначное число, где первые одна или две цифры — это день рождения, а последние две — месяц.
Историческое значение равенства в математике
Равенство – одна из основных математических операций, которая имеет огромное значение как в математике, так и за ее пределами. Идея равенства лежит в основе многих математических теорем и концепций, и она возникла задолго до создания формальной символики равенства.
Уже в древние времена ученые и математики задавались вопросом о равенстве, стараясь понять его смысл и возможности применения. Но история математики показывает, что только в 16 веке была создана символика равенства, которая существенно упростила и уточнила математические выражения.
Символ равенства (=) был введен в геометрическом трактате Роберта Рекорда в 1557 году. Он определил равенство как отношение, которое говорит о том, что два выражения представляют одно и то же число или объект. Впервые равенство было использовано для записи алгебраических равенств, но затем его применения стали расширяться на другие области математики.
Значение равенства в математике заключается в том, что оно позволяет устанавливать связи между разными математическими объектами и операциями. Равенство позволяет сравнивать и объединять числа, функции, уравнения и многое другое.
Важными свойствами равенства являются его рефлексивность, симметричность и транзитивность. Рефлексивность означает, что любой объект равен самому себе: a = a. Симметричность означает, что если a = b, то и b = a. Транзитивность означает, что если a = b и b = c, то и a = c.
Использование равенств в математике позволяет проводить логические выводы, доказывать теоремы, решать уравнения и многое другое. Равенство является одним из основных инструментов в алгебре, геометрии, математическом анализе и других разделах математики.
Как использовать знак отношения?
Знак отношения является одним из основных элементов математики и используется для определения соотношений между разными объектами и числами. Его наиболее распространенной формой является знак «равенства«, который показывает, что два объекта или числа имеют одинаковые значения.
Еще одним часто используемым знаком отношения является «больше или меньше«, который показывает, какое из двух чисел больше или меньше. Например, если мы хотим определить, какой из двух чисел больше, мы можем написать: 5 > 3.
Также знак отношения может использоваться для определения «неравенства» между числами и объектами. Например, если мы хотим определить, что одно число меньше другого, мы можем написать: 3 < 5.
Часто знак отношения используется в математических формулах и уравнениях для указания правил и соотношений между разными переменными. Также он может использоваться в графиках и диаграммах для определения отношений между разными категориями и объектами, например, в экономике для компоновки структурного уравнения и определения зависимости между разными переменными.
Важно научиться использовать знак отношения правильно и не перепутать разные формы и значения знаков. Применение знака отношения многообразно и широко используется в разных отраслях математики и науки в целом, поэтому его знание и умение применять является обязательным для людей, которые занимаются математикой и связанными с ней областями знаний
Определение равенства в математике и его особенности
Равенство в математике — это основное понятие, которое используется для сравнения и соотнесения математических выражений, объектов и данных. Оно обозначается символом «=» и имеет особые свойства и правила применения.
Основное свойство равенства — это то, что два выражения, разделенные знаком равенства, обладают одинаковыми значениями. Если математические выражения с двух сторон знака равенства идентичны и имеют одинаковые значения, то мы можем считать их равными друг другу.
Равенство в математике может применяться в различных ситуациях:
- Решение уравнений. В математике равенство используется для нахождения значений переменных в уравнениях. Путем преобразования уравнения с помощью различных математических операций можно найти значения переменных, при которых равенство выполняется.
- Доказательства. Равенство используется в математических доказательствах для установления равенства между различными выражениями или объектами. Доказывая, что два выражения равны друг другу, мы можем сделать выводы о свойствах и равенствах других объектов.
- Вычисления. Равенство позволяет производить математические операции с использованием равных выражений. Если два выражения равны друг другу, то мы можем заменять одно выражение другим в различных математических выражениях и формулах.
Однако следует отметить, что равенство в математике имеет свои особенности и ограничения:
- Равные математические выражения могут быть записаны в разных формах, но выполняться одно и то же равенство. Например, выражения «2 + 3» и «5» равны друг другу, так как они оба представляют число 5.
- Использование равенства требует соблюдения правил алгебры и математической логики. Недопустимо произвольно изменять части равенства или выполнять недопустимые операции с выражениями.
- Равенство операций выполняется по обе стороны знака равенства. Если два выражения равны друг другу, то мы можем применять одни и те же математические операции и преобразования к обоим выражениям.
Важно понимать, что равенство в математике — это не только формальная операция, но и ключевое понятие для анализа и решения математических задач и проблем. Применение правил и свойств равенства позволяет развивать математическую логику и решать сложные математические проблемы
Примеры отношения чисел
-
Сравнение чисел:
- 2
- 7 > 3 – число 7 больше числа 3;
- 4 ≤ 4 – число 4 меньше или равно числу 4;
- 9 ≥ 9 – число 9 больше или равно числу 9.
-
Пропорции:
- Если 10 яблок стоят 50 рублей, то стоимость 5 яблок будет равна 25 рублям;
- Если 8 рабочих могут выполнить задачу за 4 дня, то 16 рабочих справятся с ней за 2 дня.
-
Проценты:
- Налоговая ставка на доход составляет 20%, а повышение заработной платы составляет 10%. Тогда после повышения налоговая сумма составит 2% от повышения заработной платы;
- Если 40% учеников школы изучают французский язык, то 60% изучают другие языки.
-
Отношение чисел в математических операциях:
- Сложение: 2 + 3 = 5;
- Вычитание: 8 — 5 = 3;
- Умножение: 4 × 6 = 24;
- Деление: 12 ÷ 3 = 4.
Это лишь некоторые примеры отношений чисел, которые помогут лучше понять это важное математическое понятие
Определение соответствия
Соответствие обозначается символом «→» или стрелкой. Если элемент a из первого множества A соответствует элементу b из второго множества B, то запись будет выглядеть как a → b, где a ∈ A и b ∈ B.
Соответствие может быть задано явно в виде таблицы или графика, где каждому элементу первого множества соответствует элемент второго множества. Например, можно представить соответствие между множествами студентов и их оценками по математике.
Пример:
| Студенты | Оценки |
|---|---|
| Алиса | 5 |
| Боб | 3 |
| Кейт | 4 |
В данном примере каждому студенту соответствует его оценка по математике.
Соответствие является важным понятием в математике и используется для описания различных свойств и отношений между объектами.
Роль соответствия в математике
Соответствие в математике играет важную роль при описании отношений между различными объектами и явлениями. Оно позволяет нам сопоставлять элементы одного множества с элементами другого множества таким образом, чтобы каждому элементу первого множества соответствовал ровно один элемент второго множества.
Соответствие в математике может быть определено как набор пар элементов, где каждому элементу из первого множества соответствует ровно один элемент из второго множества. Это позволяет строить различные отношения и устанавливать взаимосвязи между объектами.
Соответствие имеет широкое применение в различных областях математики, таких как алгебра, геометрия, теория вероятностей и др. Например, в алгебре мы используем соответствие для определения функций, которые отображают элементы одного множества в элементы другого множества. В геометрии соответствие часто используется для определения подобия фигур и равенства углов.
Кроме того, соответствие помогает нам формализовать математические модели и решать различные задачи. Оно позволяет нам описывать взаимодействие объектов и представлять сложные структуры через простые соотношения.
Таким образом, соответствие является важным инструментом в математике, который помогает нам лучше понять и описать мир вокруг нас. Оно позволяет нам выявлять зависимости и устанавливать связи между объектами, что помогает нам решать сложные задачи и разрабатывать новые теории и модели.
Примеры соответствий
В математике существует множество примеров соответствий. Рассмотрим некоторые из них:
1. Соответствие между множествами чисел. Например, множество натуральных чисел N можно соотнести со множеством целых чисел Z, так как каждому натуральному числу можно сопоставить соответствующее ему целое число.
2. Соответствие между переменными. В алгебре может быть задано соответствие между переменными. Например, пусть x — переменная, тогда x² будет соответствовать квадрату этой переменной.
3. Соответствие между графиками функций. В анализе функций используются соответствия между графиками функций. Например, график функции y = sinx соответствует периодическому колебанию, а график функции y = cosx соответствует гармоническому движению.
4. Соответствие между элементами матрицы. В линейной алгебре может быть задано соответствие между элементами матрицы. Например, элемент aij матрицы А может быть соотнесен с элементом bij матрицы B, если aij равно bij.
5. Соответствие между множествами отношений. В теории множеств может быть задано соответствие между множествами отношений. Например, множество отношений R между множествами A и B соответствует функции f, если каждому элементу из множества A соответствует ровно один элемент из множества B.
Таким образом, соответствия в математике имеют широкое применение и используются для связи между объектами или явлениями в математической теории и практике. Знание и понимание соответствий позволяют построить абстрактные модели и решать разнообразные проблемы в математике.
Примеры отношений
| Пример | Описание | Иллюстрация |
|---|---|---|
| Равенство | Множество значений, которые равны друг другу. | 7 = 7 |
| Неравенство | Множество значений, которые не равны друг другу. | 3 ≠ 7 |
| Включение | Множество значений, которые включены в другое множество. | Множество B включено в множество A: B ⊆ A |
| Отношение порядка | Упорядоченное множество значений, где каждый элемент может быть сравнен с другим. | 3 < 7 |
| Функциональное отношение | Каждому значению из одного множества соответствует только одно значение из другого множества. | f(2) = 5 |
Приведенные примеры отношений помогают нам лучше понять и классифицировать математические связи между элементами множеств.
Отношение «больше»
Например, можно сравнить два числа: 5 и 3. Если 5 больше 3, то можно записать это с помощью символа «>», как «5 > 3». Такое выражение означает, что число 5 больше числа 3.
Отношение «больше» можно использовать с любыми числами: положительными, отрицательными или дробными. Например, можно сравнить числа 1.5 и -2. Если 1.5 больше -2, то можно записать это как «1.5 > -2». Такое выражение означает, что число 1.5 больше числа -2.
Отношение «больше» можно применять не только к числам, но и к переменным, выражениям и функциям. Например, можно сравнить два выражения: x + 3 и y — 2. Если x + 3 больше y — 2, то можно записать это как «x + 3 > y — 2». Такое выражение означает, что выражение x + 3 больше выражения y — 2.
Таким образом, отношение «больше» в математике позволяет сравнивать числа и выражения, определяя, какое из них является большим
Это важное понятие используется во многих математических и научных областях
| Примеры | Результат |
|---|---|
| 5 > 3 | True |
| 1.5 > -2 | True |
| x + 3 > y — 2 | Depends on the values of x and y |
Видео:ОТНОШЕНИЯ И ПРОПОРЦИИ 6 класс математикаСкачать





























