Однородные многочлены: определение и примеры

Свойства однородного многочлена

2. Сложение или вычитание однородных многочленов: При сложении или вычитании однородных многочленов получается многочлен той же степени, что и исходные многочлены.

3. Умножение однородного многочлена на число: Если однородный многочлен умножить на число, то получится однородный многочлен той же степени.

4. Знак однородного многочлена после замены переменной: Если заменить переменную в однородном многочлене, то знак его не меняется (то есть, если исходный многочлен был положительным, то и получившийся многочлен будет положительным).

5. Отсутствие однородных многочленов нулевой степени: Однородный многочлен нулевой степени не существует, так как не имеет членов с неизвестными переменными.

О числе однородных невырожденных p-ичных функций заданной степени

Пусть p простое число, F = GF(p), Vn n-мерное векторное пространство над F, е базис пространства Vn. Пусть также р: Vn ^ F. Функция р называется e-однородной, если р(х) = nv,e(x) для всех х G Vn, где nv,e однородный многочлен от n переменных над F, имеющий степень не более p 1 по каждой переменной, а x набор координат вектора х в базисе е. Функция р называется невырожденной, если deg р ^ 1 и deg dvр = (deg р) 1 для любого v G Vn \ {0}, где (dvр)(х) = р(х + v) р(х) для всех v,x G Vn. Получена формула для числа HNp(n, d) е-однородных невырожденных функций р: Vn ^ F, имеющих степень d (это число не зависит от е), а именно: если n ^ 1 и d G {1,…,n(p 1)}, n k p то HNp(n,d) = Е (-1)fcp(2)+{«dfe}p n = Е (-1)|S|pCT(S)-|S|+{n dS|}p, где k=0 SC{1…..n} n биномиальk m \ обобщённый биномиальный коэффициент порядка p dp p ный коэффициент Гаусса; ct(S) сумма всех элементов множества S. Доказано, что HNp(n, d) ^ p{d}p 1 (pn 1) (p{ d }p 1 J /(p 1) для любых d ^ 1 и jnj n ^ d/(p-1). Используя…

Еще термины по предмету «Высшая математика»

Инверсия (преобразование)

преобразование плоскости (пространства), переводящее каждую точку P в такую точку P′, лежащую на луче OP , что OP̅ · OP̅′ = c, где O — фиксированная точка (центр, или полюс инверсии) и c ≠ 0 — постоянная (коэффициент, или степень инверсии)

Индуктивное определение

способ определения множества, при котором задаются некоторые элементы определяемого множества и некоторые правила, позволяющие из имеющихся получать другие элементы этого множества; в частном случае определение понятия P (n), зависящего от натурального параметра n, протекает по следующей схеме: задаются P (0) и правило получения P (n + 1) от n и P (n); напр., факториал n! определяется так: 0! = 1, (n + 1)! = (n + 1) · n!

Круг кривизны

соприкасающийся круг

• Степень многочлена стандартного вида

• Многочлен

• Однородность

• Неприводимый многочлен

• Нулевой многочлен

• Приводимый многочлен

• Симметрический многочлен

• Невычет (невычет степени n по модулю m)

• Степень однородности поляризующего магнитного поля радиоспектрометра

• m-Learning

• Подобные члены многочлена

• Разложение многочлена на множители

• Стандартный вид многочлена

• Древостой однородный

• Однородная продукция

• Товары однородные

• Однородная структура

• Совокупность однородная

• Жидкость однородная

• Однородная функция

Однородный многочлен

Однородные многочлены от х и у ( то есть такие многочлены, у которых все члены имеют одинаковую степень) и рациональные дроби, имеющие такие члены, преобразуются введением кратных дуг, что понижает степень.
 

Однородный многочлен ( квадратичная форма), определяемый формулой ( 3), называется положительно определенным, если он принимает лишь неотрицательные значения и обращается в нуль, лишь когда все & равны нулю. Аксиома 4 требует, следовательно, чтобы квадратичная форма ( 3) была положительно определенной.
 

Однородный многочлен / равен нулю в 2п общих точках кривых К и S. Выбирая подходящим образом координаты, мы можем исключить случай, когда t оо является одной из точек пересечения S с К.
 

Однородный многочлен Р из леммы 1 является гармонической функцией.
 

Однородный многочлен Р веса л определяется своими значениями на л-мерных декартовых произведениях проективных пространств.
 

Однородный многочлен / степени г по переменным а есть линейная комбинация таких одночленов.
 

Однородный многочлен второй степени ( квадратичная форма) будет знаке / определенным, если он сохраняет постоянный знак при вещественных значениях аргументов, обращаясь в пуль только при обращении в нуль всех аргументов. Если же этот многочлен, сохраняя знак, может обращаться в нуль при значениях аргументов, не равных одновременно нулю, то он называется знакопостоянным.
 

Это однородный многочлен, степень которого равна длине кода; ои очень напоминает тэта-ряд решетки ( см. формулы ( 31) и ( 32) гл.
 

Полагая однородный многочлен и степени / от х, у, г равным r Yt, мы замечаем, что У, зависит только от координат 0, ф и является функцией положения на единичной сфере.
 

Пространство гармонических однородных многочленов степени п линейно. Это пространство, очевидно, инвариантно относительно поворотов.
 

Назовем однородным многочленом или формой степени га многочлен h ( X. Хп), все члены которого имеют одну и ту же полную степень га. Формы степеней 1, 2, 3 называются соответственно линейной, квадратичной и кубичной формами.
 

Нт — однородный многочлен ( форма) степени т относительно координат и импульсов. Аддитивная постоянная ( равная значению функции Гамильтона в положении равновесия) не влияет на уравнения движения и в разложении ( 44) отброшена.
 

Число членов однородного многочлена ( 1) равно С, при этом считаются и те члены многочлена, у которых коэффициент равен нулю.
 

Это свойство однородных многочленов может служить основанием для очень полезного расширения понятия однородности функции.
 

Рз являются однородными многочленами степеней 30, 20 и 12 соответственно. Нули многочлена рз в проективном пространстве, состоящем из всех прямых, проходящих через начало координат в С2, образуют двенадцать вершин правильного икосаэдра, нули многочлена р2 образуют средние точки двадцати граней этого икосаэдра, а нули многочлена р образуют средние точки тридцати ребер этого икосаэдра.
 

Умножение одночлена на многочлен

Напомним распределительный закон умножения:

Используя этот закон, можно производить умножение одночлена на многочлен.

Пример. Перемножьте выражения 5v2 и 9v3 + 2t4.

Решение: Запишем произведение выражений:

Такое раскрытие скобок можно объяснить с помощью «метода фонтанчика»:

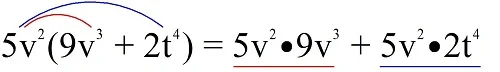
От множителя 5v2 строят линии (синего цвета к) КАЖДОМУ слагаемому в скобке. Каждой такой линии соответствует отдельное произведение в получаемом полиноме.

После раскрытия скобок получили два произведения одночлена на одночлен, которые считаем по отдельности (см. урок 3):

Можно сформулировать следующее правило умножения многочлена на одночлен:

Ещё один пример. Перемножьте полином 2x2y + 4xy2 – 1 и моном – 3ху.

Решение:

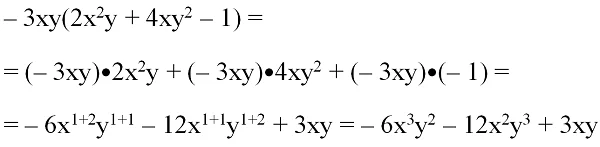
Здесь метод «фонтанчика» будет выглядеть так:

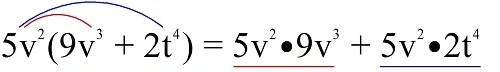
Можно заметить, что после умножения монома на полином получится столько одночленов, сколько их было в исходном полиноме. Это правило можно использовать для самоконтроля.

Значение однородных многочленов в математике

Значение однородных многочленов в математике заключается в их специальных свойствах и возможности проведения различных операций. Однородные многочлены позволяют упростить алгебраические расчеты и решать задачи с использованием симметрии и групповых операций.

Одним из основных свойств однородных многочленов является то, что если мы заменим все переменные на их множители вещественного числа, то значение многочлена не изменится. Например, если у нас есть однородный многочлен $3x^2 + 4xy — 2y^2$, и мы заменим переменные $x$ и $y$ на их множители вещественного числа $\alpha$, то мы получим многочлен $3\alpha^2 + 4\alpha\beta — 2\beta^2$.

Однородные многочлены находят применение в различных областях математики, физики и других наук. Например, они используются в теории многочленов для анализа и решения уравнений, в теории вероятностей и статистике для моделирования случайных явлений, а также в теории игр для описания и анализа стратегий и ситуаций.

Примеры однородных многочленов	Иллюстрации
$2x^2 — 5xy + 3y^2$
$4x^3 — 2x^2y + 5xy^2 — 3y^3$
$7x^4 — 3x^3y + 6x^2y^2 — 2xy^3 + 4y^4$

Это лишь несколько примеров однородных многочленов и их иллюстраций, которые помогут визуализировать и понять суть этого понятия.

Умножение многочлена на многочлен

Пусть нам надо перемножить два полинома, a+bи c+d. Запишем их произведение:

Заменим выражение a + b переменной k:

Теперь исходное произведение можно выразить как произведение монома и полинома:

Проведем обратное преобразование, заменив k на a + b:

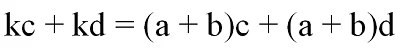
Наконец, раскроем скобки в этом выражении:

Эту формулу можно проиллюстрировать геометрически. Рассмотрим прямоугольник со сторонами a + b и c + d:

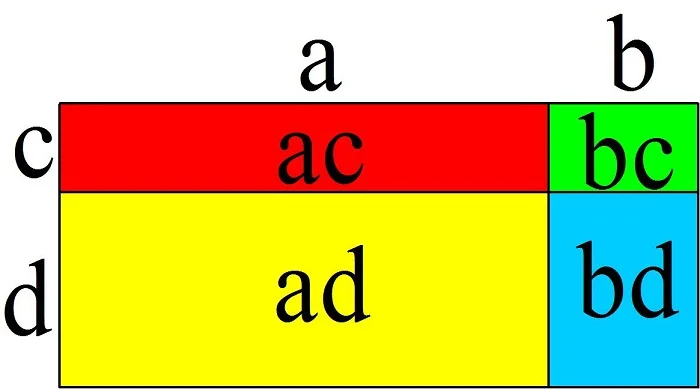
Площадь этого прямоугольника, как и любого другого, равна произведению его сторон, то есть(a + b)(c + d).С другой стороны, она состоит из 4 прямоугольников, чьи площади также вычисляются как произведения их сторон, и составляют ac, bc, ad и bd. Поэтому можно записать равенство

Получается, что для умножения многочлена на многочлен нужно перемножать попарно все мономы, входящие в их состав, после чего сложить их.

Если в одном полиноме содержится m слагаемых, а в другом n, то результатом их перемножения окажется новый полином, содержащий m•n мономов (до приведения подобных слагаемых). Для перемножения многочленов также используется метод «фонтанчика».

Пример. Найдем произведение выражений 3a2 – 4ab + b2и 2a– b.

Решение: В первом полиноме содержится 3 монома, а во втором – 2, поэтому после их перемножения мы получим сумму 3•2 = 6 одночленов:

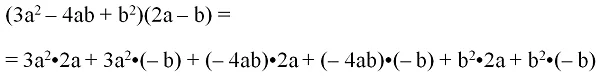
Раскрытие скобок «фонтанчиком» будет выглядеть так:

В результате действительно получилась сумма 6 мономов. Осталось вычислить каждый из них, после чего привести подобные слагаемые:

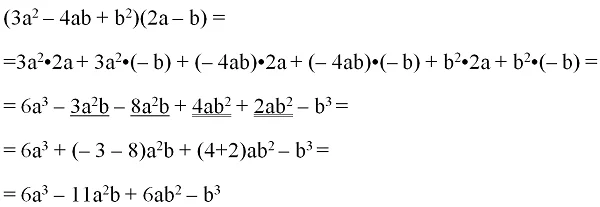
Заметим, что при перемножении полиномов происходит сложение степеней многочленов. Действительно, в рассмотренном выше примере мы умножили полином второй степени 3a2 – 4ab + b2 на полином первой степени 2a– b, и получили в результате многочлен 3-ей (2+1) степени.

Также возможно умножение многочленов в столбик. Особенно это удобно делать в случае с полиномами с одной переменной.

Пример. Найдите произведение выражений 2×3 + 3×2 +5x + 9 и x2 + 4x + 7.

Решение: Запишем полиномы в столбик, один под другим:

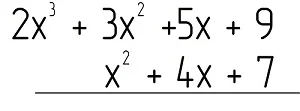
Далее умножим самый правый моном второго многочлена, то есть число 7, на первый полином, и запишем его ниже:

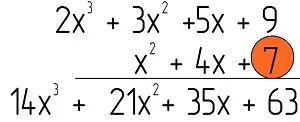
Далее умножим следующий моном, 4х, на первый полином, и запишем результат ещё ниже, причем сместим запись чуть влево, чтобы подобные члены оказались друг под другом:

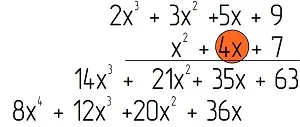
Также умножим последний одночлен, x2, на первый полином:

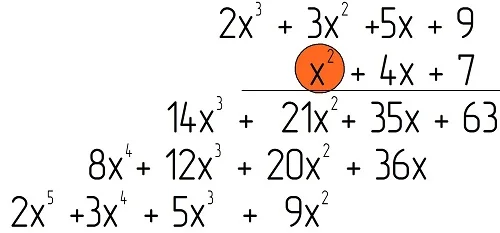
Осталось сложить подобные слагаемые (то есть переменные х с одинаковыми степенями), которые записаны друг под другом:

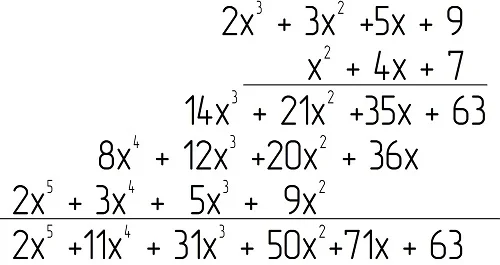
Ещё раз цветом выделим подобные слагаемые и результаты их суммирования:

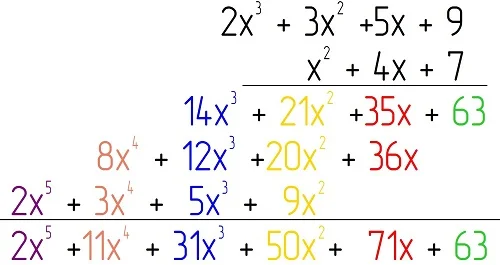
Ответ: 2х5 + 11х4 + 31х3 + 50х2 + 71х +63.

Сложение и вычитание многочленов

Полиномы можно складывать друг с другом, а также вычитать. При этом, возможно, придется приводить подобные слагаемые.

Пример. Произведите сложение многочленов 8z2 + 3z +12 и 2z4 + 9z.

Решение. Запишем интересующую нас сумму:

Если перед скобками стоит знак «+», то можно просто опустить скобки:

Осталось привести полином к стандартному виду. Здесь есть лишь одна пара подобных одночленов, 3z и 9z:

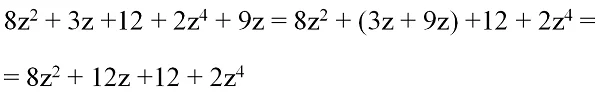
При вычитании многочленов надо учитывать следующее правило:

Пример. Вычтите из полинома x5 + 3×3– 7y3 + 9×2 + 17 трехчлен 2y4 + 0,4y3– 25.

Решение:

Запишем разность полиномов:

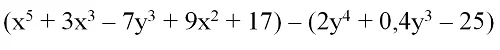
Первые скобки можно опустить, так как перед ними нет никакого знака. Перед вторыми скобками стоит минус, а потому для раскрытия скобок знаки слагаемых в них надо поменять на противоположные. Вместо 2y4 надо написать – 2y4, вместо 0,4y3 поставим – 0,4y3, а – 25 заменим на + 25:

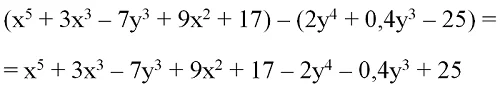
Осталось привести подобные слагаемые:

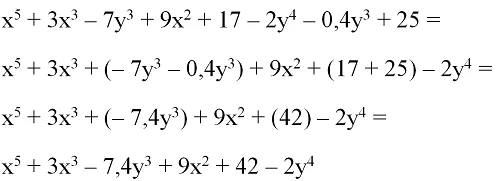
Стоит заметить, что при сложении и вычитании полиномов их степени не могут увеличиться. Так, если складываются два полинома 5-ой и 4-ой степени, то в результате получится многочлен, чья степень будет не больше 5.

Рассмотрим более сложный пример с вложенными (внутренними) скобками. Необходимо упростить выражение

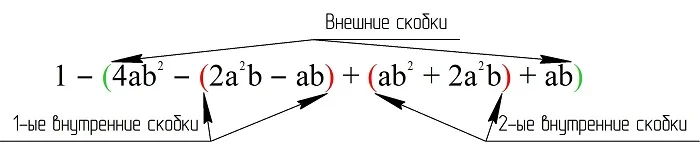
Решение. Раскроем первые скобки. Перед ними стоит минус, поэтому знаки слагаемых должны поменяться на противоположные

Однако обратите внимание, что здесь есть вложенные скобки (2a2b – ab) и (ab2 + 2a2b). Менять следует только знак перед ними, а знаки внутри вложенных скобок не меняются! Они рассматриваются как единые, неизменяемые слагаемые:

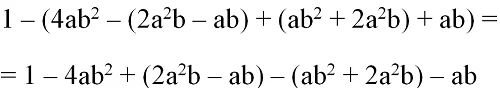
Теперь раскроем оставшиеся две скобки:

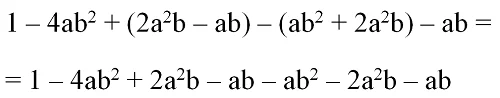
Приведем подобные слагаемые. Для наглядности пары подобных мономов подчеркнуты. Одной чертой подчеркнуты мономы с буквенной частью ab2, двумя чертами – мономы с a2b, а штриховой линией выделены мономы с буквенной частью ab:

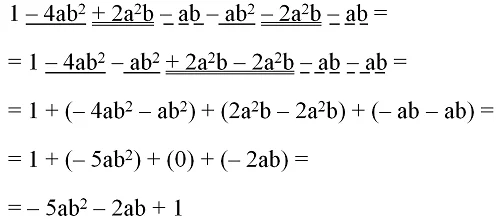
Использование в алгебраической геометрии

Подобно тому, как аффинное алгебраическое многообразие на K является местом сокращения в аффинном пространстве K n семейства многочленов от n переменных с коэффициентами в K , проективное алгебраическое многообразие на K является местом сокращения в проективном пространстве P _п ( К ), семейство однородных многочленов с п + 1 переменных с коэффициентами в K .

Например, можно определить алгебраическую кривую аффинное K 2 как место отмены многочлена от двух переменных с коэффициентами в K . Если мы хотим определить алгебраическую кривую в проективной плоскости P ₂ ( K ), мы также хотели бы определить ее как геометрическое место сокращения многочлена P от трех переменных. Но в проективной плоскости (λ x : λ y : λ z ) = ( x : y : z ) для всех λ ≠ 0. Следовательно, мы обязательно хотим, чтобы P ( x , y , z ) = 0 ⇔ P (λ x , λ y , λ z ) = 0, так что место сокращения не зависит от выбранного λ. Вот почему мы требуем, чтобы многочлен P был однородным.

Однородный многочлен первой степени

F(x) = a₁x + a₂x + … + a_nx

Где a₁, a₂,…, a_n – коэффициенты многочлена, а x – переменная, которая возводится в степень.

Однородные многочлены первой степени также называют линейными многочленами или линейными уравнениями. Они имеют простую форму и применяются для описания линейных зависимостей между двумя переменными.

Примером однородного многочлена первой степени может служить следующее уравнение:

F(x) = 2x + 3

В этом примере коэффициент a равен 2, а переменная x возводится в степень 1. Из этого уравнения можно сделать вывод, что при увеличении значения x на 1, значение функции F(x) увеличится на 2.

Однородные многочлены первой степени широко применяются в различных областях, таких как математика, физика, экономика и т.д. Они позволяют моделировать простые линейные зависимости между величинами и решать соответствующие задачи.

Универсальное обобщение алгоритма цепной дроби

Простое обобщение. Пусть в трехмерном вещественном пространстве заданы три вещественные однородные линейные формы. Их модули дают отображение этого пространства в другое. В нем рассматривается выпуклая оболочка образов всех целочисленных точек первого пространства, кроме его начала координат. Замыкание этой выпуклой оболочки названо модульным многогранником. Наилучшие целочисленные приближенияккорневымподпространствам заданныхформдаютточки,образы которыхлежатнаграницемодульногомногогранника.Границамодульного многогранника вычисляется любой стандартной программой вычисления выпуклых оболочек. Алгоритм дает также периодичность для кубическихиррациональностей сположительным дискриминантом. Обобщить цепную дробь пытались Эйлер, Якоби, Дирихле, Эрмит, Пуанкаре, Гурвиц, Клейн, Минковский, Вороной и многие другие. Универсальное обобщение. Пусть в n-мерном вещественном пространстве R n заданы l линейных и k квадратичных форм (n = l +2k). Модули этих форм задают отображение пространства R n …

Пример 2: Однородные многочлены с одинаковым старшим членом

Примером однородного многочлена с одинаковым старшим членом является многочлен:

4x^3 + 2x^2 — 3x^3 + 5x^2 + x^3

В данном случае старший член многочлена, выделенный жирным шрифтом, это 4x^3. Все остальные члены многочлена также имеют степень 3 и одинаковые переменные x. Такой многочлен можно упростить, сгруппировав члены с одинаковым старшим членом:

4x^3 — 3x^3 + x^3 + 2x^2 + 5x^2

Результирующий многочлен будет иметь вид:

2x^3 + 7x^2

Таким образом, данный пример демонстрирует однородность многочлена с одинаковым старшим членом, а также позволяет провести операцию упрощения и приведения подобных членов.

Многочлен, вычисление значений многочлена

В предыдущем уроке мы познакомились с понятием одночлена. При записи одночленов не используется операция сложения. Если же возникает необходимость сложить несколько одночленов, то в результате получается многочлен.

В качестве примера многочленов можно привести следующие выражения:

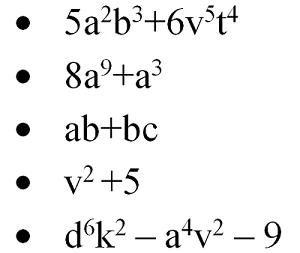
Стоит обратить внимание, что в записи многочлена может использоваться и знак минус, при этом его всё равно можно считать суммой одночленов, а не разностью. Дело в том, что можно условно считать, что знак минус относится к коэффициенту одночлена, например:

Для некоторых видов многочленов существуют особые названия. Если многочлен состоит из двух одночленов, то его называют двучленом. Многочлен, состоящий из 3 одночленов, называют трехчленом.

Иногда в литературе используются такие термины, как «моном» (синоним «одночлена»), «бином» (синоним «двучлена»), «полином» (синоним «многочлена»).

Если известно значение переменных, входящих в полином, то возможно вычисление значения многочлена.

Пример. Найдем значение полинома x3+2×2+5y+1 при значении x=2 и y = 3.

Решение.

Пример. Вычислим значение полинома v4– d4при значении переменных v = 4 и d = 3.

Решение.

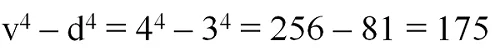
Примеры применения однородного многочлена

Однородный многочлен – это многочлен, каждый из членов которого однороден по степени. Использование однородности многочлена позволяет сократить количество свободных переменных и упростить решение уравнения.

Одним из примеров применения однородного многочлена является задача о вычислении площади круга. Если рассмотреть уравнение круга в полярных координатах, то его можно представить в виде однородного многочлена второй степени. Таким образом, при решении этой задачи можно использовать свойства однородных многочленов и получить более простую формулу для площади круга.

Другим примером применения однородных многочленов являются уравнения Максвелла в электродинамике. Они выражают законы электромагнетизма и описывают поведение электрических и магнитных полей. Уравнения Максвелла являются однородными многочленами четвертой степени и обладают рядом свойств, которые позволяют получать новые решения на основе уже известных.

• Площадь круга
• Уравнения Максвелла в электродинамике

Также однородные многочлены используются в задачах оптимизации и математической физике. Они позволяют получать более удобные формы для уравнений и решать их с помощью общих методов решения. Например, в задачах о нахождении экстремумов функций однородные многочлены часто выполняют роль ограничений на допустимые значения переменных.

Области применения однородных многочленов
Математическая физика
Оптимизация

В заключение можно отметить, что однородные многочлены являются важным инструментом в математике и находят применение во многих областях. Понимание свойств и особенностей этих многочленов позволяет решать задачи с большей точностью и эффективностью.