Что значит продольная ось

Визуальное представление осей в геометрии

Ось в геометрии является прямой линией, которая проходит через точку и имеет определенное направление. Оси широко используются в геометрии для определения положения и направления объектов.

Визуальное представление осей может быть представлено различными способами. Одним из наиболее часто используемых способов является использование координатной плоскости. Координатная плоскость состоит из двух перпендикулярных осей — горизонтальной оси (ось абсцисс) и вертикальной оси (ось ординат).

Ось	Направление	Представление
Ось абсцисс	Горизонтальная	X
Ось ординат	Вертикальная	Y

Оси абсцисс и ординат пересекаются в центре координатной плоскости, которая обозначается буквой O. Этот центр является точкой отсчета для определения координат всех других точек на плоскости. Точки, находящиеся выше оси ординат, имеют положительные значения по оси Y, а точки, находящиеся ниже этой оси, имеют отрицательные значения по оси Y. Аналогично, точки, находящиеся правее оси абсцисс, имеют положительные значения по оси X, а точки, находящиеся левее этой оси, имеют отрицательные значения по оси X.

Визуальное представление осей позволяет легко определять положение объектов на координатной плоскости и проводить различные геометрические манипуляции, такие как нахождение расстояния между двумя точками или построение графиков функций.

Примеры использования поперечного направления

Существует ли простой способ, чтобы запомнить разницу между поперечным и продольным направлением?

Да, есть простой способ запомнить разницу между поперечным и продольным направлением. Представьте себе, что вы находитесь на перекрестке и переходите дорогу, двигаясь поперек пути движения транспорта. Это поперечное направление. А теперь представьте, что вы идете по длинной улице, двигаясь вперед, вдоль улицы. Это продольное направление.

Поперечное направление играет важную роль во многих сферах нашей жизни. Вот несколько примеров, где знание поперечного направления может быть очень полезным:

1. Дорожное движение: Запомните, что поперечно направление соответствует пешеходному переходу, а продольно — движению автомобилей. Поперечное направление будет также указывать на перпендикулярность между дорогой и прилегающими улицами. Выучите эти правила и сдать экзамен по ПДД будет намного проще!

Как запомнить разницу между поперечным и продольным направлением?

Простой способ запомнить разницу между поперечным и продольным направлением — это представить себе поперечный проход в перекрестке, а продольный — прямую дорогу, вдоль которой можно двигаться.

2. Работа с деревом или металлами: Поперечное направление часто используется для обозначения сечения дерева или металла. Например, при работе с деревом поперечное направление указывает на направление, перпендикулярное росту дерева, а продольное — вдоль роста.

3. Медицина: Поперечное направление может использоваться для описания местоположения органов тела. Например, поперечное сечение живота будет перпендикулярно продольной плоскости тела.

4. Работа с картами и компасами: При использовании компаса или чтении карты, поперечное направление поможет вам определить коротчайший путь или разницу между двумя точками. Следуйте поперечному направлению и не заблудитесь!

5. Изучение основ: При изучении новой темы или конспектировании уроков, поперечное направление может помочь вам облегчить запоминание информации. Используйте стишки-запоминалки или создайте схемы и рисунки, чтобы лучше запомнить содержание.

Важно понимать разницу между поперечным и продольным направлением и уметь применять эту информацию в нужных ситуациях. Сравните различия и запомните, что поперечное направление пересекает другие направления, а продольное направление соответствует идущему вперед

Не забывайте об этом при решении задач и подготовке к экзаменам!

Оси Декартовой системы координат

Горизонтальная ось X направлена вправо от начала координат, а вертикальная ось Y направлена вверх. Координата на оси X может принимать любое значение отрицательное или положительное, аналогично координата на оси Y.

Оси Декартовой системы координат часто используются для отображения геометрических фигур, графиков функций и других математических объектов. Они позволяют точно определить положение объекта в пространстве.

Горизонтальная ось

В геометрии горизонтальная ось используется для описания координатной системы. Она простирается горизонтально от левой части координатной плоскости до правой части. Горизонтальная ось обычно называется осью X или горизонтальной осью. Она позволяет определять положение точек на плоскости с помощью двух координат — координата X и координата Y.

В физике горизонтальная ось используется для изучения движения. Она помогает определить начальное положение и изменение положения объекта с течением времени. Например, при изучении броска мяча горизонтальная ось используется для измерения расстояния, которое пройдет мяч по горизонтали.

В географии горизонтальная ось используется для определения широты. Широта — это угол, измеряемый от экватора до данной точки на земной поверхности. Горизонтальная ось позволяет измерять и указывать широту северной и южной полушарий.

В технике горизонтальная ось используется для расположения элементов на плоскости или поверхности. Например, при проектировании деталей машин горизонтальная ось используется для указания положения отверстий, вырезов или других элементов.

Вертикальная ось

Основные свойства, относящиеся к вертикальной оси:

• margin-top: задает отступ от верхнего края элемента;
• margin-bottom: задает отступ от нижнего края элемента;
• padding-top: задает внутренний отступ от верхнего края элемента;
• padding-bottom: задает внутренний отступ от нижнего края элемента;
• height: задает высоту элемента;
• top: задает позицию элемента относительно верхней границы родительского элемента;
• bottom: задает позицию элемента относительно нижней границы родительского элемента.

Вертикальная ось позволяет управлять вертикальным позиционированием элементов на странице. С помощью указанных свойств можно задавать отступы, высоту элементов и их позицию относительно родительского элемента.

Направления осей

Оси могут иметь различные направления в зависимости от конкретной системы координат. В классической системе координат, такой как декартова система координат, оси обычно направлены вдоль горизонтальной и вертикальной оси.

В декартовой системе координат горизонтальная ось называется осью X, а вертикальная ось — осью Y. Ось X обычно направлена вправо, а ось Y — вверх. Такая ориентация осей позволяет однозначно задавать положение точек на плоскости.

Однако, в некоторых других системах координат, например, в полярной системе координат, направления осей могут быть иными. В полярной системе координат ось, обозначающая расстояние от начала координат, направлена от начала координат наружу. Другая ось, обозначающая угол, может быть направлена в разных направлениях в зависимости от выбранной конвенции.

Важно помнить, что направления осей могут быть произвольными, и конкретная система координат может иметь свои собственные соглашения относительно направлений осей

Примеры осей в геометрии

Ось симметрии

Осью симметрии называется прямая, вокруг которой выполняется симметричное отображение фигуры. Например, у круга или равнобедренного треугольника с основанием, параллельным оси ординат, будет существовать ось симметрии.

Ось вращения

Осью вращения называется прямая, вокруг которой выполняется поворот фигуры. Например, у цилиндра осью вращения является прямая, параллельная оси ординат и проходящая через его основания.

Оси симметрии многогранников

У многих многогранников, таких как куб, правильный тетраэдр или октаэдр, существует несколько осей симметрии. Например, у куба всего 9 осей симметрии – 3 оси, параллельные осям координат, и 6 осей, проходящих через середины противоположных граней.

Симметрали

Симметралями называются прямые, перпендикулярные основной оси симметрии, которые разделяют фигуру на две равные части. Например, у прямоугольника с основаниями, параллельными осям координат, симметралями будут серединные перпендикуляры к его сторонам.

Примеры осей в геометрии
Фигура
Тип оси

Круг
Ось симметрии

Равнобедренный треугольник
Ось симметрии

Цилиндр
Ось вращения

Куб
Ось симметрии

Прямоугольник
Симметрали

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж:
Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.

Внутренние силы. Метод сечений.

Действие на тело внешних сил приводит к его деформации (меняется взаимное расположение частиц тела). Вследствие этого между частицами возникают дополнительные силы взаимодействия. Это силы сопротивления изменению формы и размеров тела под действием нагрузки, называют внутренними силами (усилиями). С увеличением нагрузки внутренние усилия возрастают. Выход из строя элемента конструкции наступает при превышении внешних сил некоторого предельного для данной конструкции уровня внутренних усилий. Поэтому оценка прочности нагруженной конструкции требует знания величины и направления возникающих внутренних усилий. Значения и направления внутренних сил в нагруженном теле определяют при заданных внешних нагрузках методом сечений.

Метод сечений (см. рис. 2) состоит в том, что брус, находящийся в равновесии под действием системы внешних сил, мысленно рассекают на две части (рис. 2, а), и рассматривают равновесие одной из них, заменяя действие отброшенной части бруса системой внутренних сил, распределенных по сечению (рис. 2, б). Заметим, что внутренние силы для бруса в целом, становятся внешними для одной из его частей. Причем во всех случаях внутренние усилия уравновешивают внешние силы, действующие на отсеченную часть бруса.

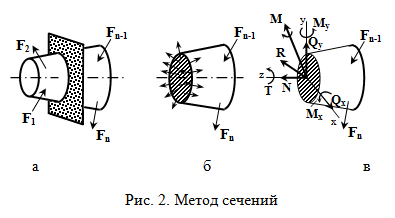
В соответствии с правилом параллельного переноса сил статики приведем все распределенные внутренние силы к центру тяжести сечения. В результате получим их главный вектор R и главный момент M системы внутренних сил (рис. 2, в). Выбрав систему координат O_xyz так, чтобы ось z являлась продольной осью бруса и проецируя главный вектор R и главный момент M внутренних сил на оси, получим шесть внутренних силовых факторов в сечении бруса: продольную силу N, поперечные силы Q_x и Q_y, изгибающие моменты М_x и M_y, а также крутящий момент Т. По виду внутренних силовых факторов можно определить характер нагружения бруса. Если в поперечных сечениях бруса возникает только продольная сила N, а другие силовые факторы отсутствуют, то имеет место «растяжение» или «сжатие» бруса (в зависимости от направления силы N). Если в сечениях действуют только поперечная сила Q_x или Q_y — это случай «чистого сдвига». При «кручении» в сечениях бруса действуют только крутящие моменты Т. При «чистом изгибе» — только изгибающие моменты М. Возможнытакже комбинированные виды нагружения (изгиб с растяжением, кручение с изгибом и др.) – это случаи «сложного сопротивления». Для наглядного представления характера изменения внутренних силовых факторов вдоль оси бруса строят их графики, называемые эпюрами. Эпюры позволяют определить наиболее нагруженные участки бруса и установить опасные сечения.

Основные принципы работы оси в механизмах

Ось является одним из важнейших элементов в технической механике. Она представляет собой вращающееся цилиндрическое тело, которое используется для передачи механической энергии или как опора для других элементов.

Основные принципы работы оси в механизмах включают:

1. Передача механической энергии: Ось может служить для передачи механической энергии от одного элемента механизма к другому. Например, в велосипеде ось вращения педалей передает энергию от ног плиты к колесу.
2. Соединение двух или более элементов: Ось может использоваться для соединения двух или более элементов механизма. Например, в автомобиле оси вращения передних и задних колес связывают друг с другом и обеспечивают передвижение автомобиля.
3. Осевое перемещение: Ось может быть использована для осевого перемещения других элементов механизма. Например, в зубчатом механизме ось перемещает зубчатые колеса, изменяя отправную точку зубчатого зацепления и реализуя передачу движения.
4. Создание стержневой опоры: Ось может быть использована для создания стержневой опоры, обеспечивая устойчивость других элементов механизма и поддерживая их положение.

Применение оси в механизмах широко распространено. Они используются во многих областях, включая промышленность, автомобилестроение, машиностроение, электротехнику и другие. Оси могут быть изготовлены из различных материалов, таких как металлы, пластик и композиты, в зависимости от требуемых характеристик и условий эксплуатации.

Применение оси в различных отраслях промышленности

Ось, как конструктивный элемент, широко применяется в различных отраслях промышленности и играет важную роль в многих работах. В данном разделе рассмотрим несколько примеров использования оси в разных сферах деятельности.

Машиностроение и автомобильная промышленность:

• В машиностроении оси используются в различных механизмах и машинах для передачи момента силы и обеспечения вращения. Они применяются, например, в двигателях, трансмиссиях и приводах.
• В автомобильной промышленности оси играют важную роль в системе подвески, обеспечивая стабильность и маневренность автомобиля.

Судостроение:

В судостроении оси применяются для передачи силы от двигателей к винтам и рулевым устройствам судна. Они обеспечивают движение и маневренность судна.

Энергетика:

В энергетике оси используются в различных механизмах и оборудовании: в турбинах, генераторах, насосах и других устройствах, где необходимо передавать вращение.

Горнодобывающая промышленность:

В горнодобывающей промышленности оси применяются в шахтных лебедках для подъема и опускания грузов.

Производство и строительство:

• В производстве оси используются в различных станках и механизмах для обеспечения вращения и передачи силы.
• В строительстве оси применяются в строительных машинах и оборудовании: кранах, буровых установках, подъемниках, гидравлических системах и т.д.

Это лишь несколько примеров применения оси в различных отраслях промышленности. Она является неотъемлемой частью многих механизмов и оборудования, обеспечивая надежную и эффективную работу.

Физическое понятие продольной силы

Продольная сила – это физическая величина, которая возникает при взаимодействии объектов или частей объекта и направлена вдоль их оси. Продольная сила может быть как внешней, действующей на объект извне, так и внутренней, возникающей внутри самого объекта.

Продольная сила является одной из основных характеристик механического взаимодействия. Она может возникать при различных ситуациях, таких как торможение, разгон, движение по наклонной плоскости и др.

В случае статических систем действующих продольных сил можно различить два основных вида распределения сил: равномерное и неравномерное распределение. При равномерном распределении силы равномерно распределены по всей длине объекта или его части. В случае неравномерного распределения силы, сила меняется вдоль длины объекта или его части.

Продольная сила может быть представлена в виде эпюры, которая позволяет визуализировать и анализировать ее распределение вдоль объекта. Эпюра – это графическое изображение продольных сил, наложенных на объект или его части. С помощью эпюры можно определить максимальную и минимальную силу, точки интенсивного действия силы и т.д.

Чтобы построить эпюру продольной силы, необходимо знать значения силы в различных точках объекта и соединить эти точки с помощью ломаной линии.

Использование эпюр продольных сил позволяет визуализировать и анализировать распределение продольных сил в объекте или его части, что помогает в дальнейшем проектировании и оптимизации механических систем.

Продольная ось и силовые факторы

Продольная ось также связана с определенными силовыми факторами, такими как рыскание и вращение. Рыскание — это вращение самолета или другого транспортного средства вокруг его вертикальной оси, которая перпендикулярна продольной оси. Вращение вокруг продольной оси играет важную роль в управлении и маневрировании.

Продольная ось также связана с различными историями проблем в инженерии. Например, Журавский и Верещагина предложили метод дифференциальных уравнений, которые учитывают динамические деформации в продольной оси при расчетах прочности транспортных средств. Продольная ось также связана с транспортными системами, в которых изгибная прочность оси является ключевым фактором.

Продольно и поперечно: разница и примеры

В механике и строительстве термины «продольно» и «поперечно» используются для обозначения направления или ориентации движения или расположения объектов в пространстве. Разница между ними заключается в том, как они определяются относительно оси или плоскости.

Продольно означает вдоль направления оси или линии. При использовании этого термина объекты располагаются или движутся в направлении оси или линии. Например, «двигаться продольно» означает двигаться вдоль оси или линии, а «расположиться продольно» означает расположиться вдоль оси или линии.

Поперечно означает поперек или перпендикулярно к оси или плоскости. Этот термин описывает направление, перпендикулярное к направлению оси или линии. Например, «двигаться поперек» означает двигаться поперек оси или линии, а «расположиться поперек» означает расположиться перпендикулярно к оси или линии.

Простыми словами, если нарисовать ось или линию в горизонтальном направлении, то «продольно» будет означать движение или расположение вдоль этой оси, а «поперечно» будет означать движение или расположение перпендикулярно данной оси.

Примеры использования этих терминов могут быть различными в разных контекстах. Например, в автомобильной промышленности термины «продольные» и «поперечные» ссылаются на расположение или направление передней и задней части автомобиля. «Продольный двигатель» означает двигатель, расположенный вдоль или параллельно оси автомобиля, а «поперечный двигатель» означает двигатель, расположенный поперек оси автомобиля.

Другой пример может быть в строительстве. «Продольная стенка» означает стенку, которая располагается вдоль длины помещения, а «поперечная стена» означает стенку, которая располагается поперек помещения, перпендикулярно к длине.

Использование терминов «продольно» и «поперечно» зависит от контекста и области применения. Понимание этих терминов позволяет точнее описывать направление и ориентацию объектов в пространстве.

График квадратичной, кубической функции, график многочлена

Поперечная ось: примеры в строительстве

Одним из примеров применения поперечной оси является использование её в системах железнодорожного транспорта. Поперечная ось в транспортных средствах важна для обеспечения устойчивости и предотвращения рыскания и вращения вокруг вертикальной оси. Она позволяет удерживать транспортные средства на рельсах и обеспечивает безопасность пассажиров и грузов.

В авиации также существует пример применения поперечной оси. В процессе полета самолета, поперечная ось помогает ему удерживаться в прямом положении и не отклоняться от заданного курса. Она играет ключевую роль при выполнении маневров, таких как рулон, когда самолет наклоняется вокруг продольной оси.

Еще одним примером применения поперечной оси является строительство зданий и мостов. В этих конструкциях поперечная ось играет важную роль в расчетах напряжений и деформаций. Она позволяет определить коэффициент изгиба, коэффициент Пуассона и другие факторы, которые влияют на прочность конструкции. С помощью поперечной оси также определяются силовые и перемещения на этих сооружениях.

Пример применения поперечной оси можно найти и в строительстве гидроциклов и других водных средств. Поперечная ось позволяет удерживать гидроцикл в прямом положении и обеспечивает его устойчивость при движении по воде.

Таким образом, поперечная ось имеет множество применений в различных областях, включая строительство зданий и мостов, транспортные системы и авиацию. Она является важным инструментом при расчетах и проектировании конструкций, а также обеспечивает безопасность и стабильность в различных ситуациях.

Ось в технической механике:

Ось — это элемент конструкции, представляющий собой деталь соосного соединения двух или более частей механизма. Оси используются для передачи силы, вращения и поддержания точного положения различных деталей механизма.

Оси могут быть изготовлены из различных материалов, таких как сталь, алюминий, чугун и т. д. Они обычно имеют цилиндрическую форму и могут быть полыми или заполненными. Оси могут быть одиночными или соединены вместе с помощью втулок или других элементов.

Оси играют важную роль в работе механизмов. Они обеспечивают жесткую связь между двумя или более деталями, позволяют им вращаться относительно друг друга и переносить механическую нагрузку. Оси также позволяют точно выставить нужное положение деталей и предотвратить их смещение.

Применение осей в технической механике очень обширно. Они используются в различных отраслях промышленности, таких как машиностроение, автомобилестроение, судостроение и т. д. Оси находят применение как в крупных механизмах, так и в мелких инструментах и бытовой технике.

Одним из примеров применения оси является вращение колес на автомобиле. Колеса устанавливаются на оси, которые в свою очередь крепятся к подвеске автомобиля. Оси позволяют колесам свободно вращаться и переносить груз автомобиля.

Еще одним примером применения осей является механизм часов. Внутри механизма находятся различные оси, которые позволяют стрелкам двигаться и указывать время. Оси в часах обеспечивают точное положение стрелок и их вращение.

В заключение, оси представляют собой важный элемент в технической механике и широко используются в различных механизмах. Они обеспечивают передачу силы и вращения, а также поддерживают точное положение деталей. Без осей многие механизмы не смогли бы работать эффективно.

Ссылки

1. Хеллебрандт, Ф. А., Теппер, Р. Х., Браун, Г. Л., и Эллиотт, М. С. (1938). Расположение основных плоскостей анатомической ориентации, проходящих через центр тяжести у молодых взрослых женщин.Американский журнал физиологии — наследие, 121(2), 465-470.
2. Каппоццо А., Катани Ф., Делла Кроче У. и Лирдини А. (1995). Положение и ориентация в пространстве костей при движении: определение и определение анатомической структуры.Клиническая биомеханика, 10(4), 171-178.
3. Мирджалили, С. А., Макфадден, С. Л., Бакенхэм, Т., Уилсон, Б., и Стрингер, М. Д. (2012). Анатомические планы: преподаем ли мы точную анатомию поверхности?Клиническая анатомия, 25(7), 819-826.
4. Ачар, Х. И., Кёмерт, А., Авсар, А., Челик, С., и Кузу, М. А. (2014). Динамическая статья: хирургические анатомические планы полного мезоколенного иссечения и прикладная анатомия сосудов правой ободочной кишки.Заболевания толстой и прямой кишки, 57(10), 1169-1175.
5. Додсон, М. Г., и Детер, Р. Л. (1990). Определение анатомических плоскостей для использования в трансвагинальной сонографии.Журнал клинического ультразвука, 18(4), 239-242.
6. Эванс, А. С., Бейл, К., Маррет, С., Томпсон, К. Дж., И Хаким, А. (1988). Анатомо-функциональная корреляция с использованием настраиваемого атласа интересующей области на основе МРТ с позитронно-эмиссионной томографией.Журнал церебрального кровотока и метаболизма, 8(4), 513-530.
7. Узун, К., Атман, Э. Д., Устунер, Э., Мирджалили, С. А., Озтуна, Д., и Эсмер, Т. С. (2016). Анатомия поверхности и анатомические плоскости у взрослого населения Турции.Клиническая анатомия, 29(2), 183-190.
8. Рейнольдс, Х. М., и Хаббард, Р. П. (1980). Анатомические системы координат и биомеханика.Человеческие факторы, 22(2), 171-176.