Основания треугольника: что это такое и как их найти?

Применение в науке и технике

Группа геометрических тел имеет широкое применение в науке и технике. Различные формы и свойства этих тел позволяют использовать их в разных областях.

Одним из наиболее распространенных применений геометрических тел является использование их в архитектуре и строительстве. Например, при проектировании зданий используются различные формы и комбинации геометрических тел для создания устойчивых и эстетически привлекательных конструкций.

Геометрические тела также находят применение в машиностроении. Например, при проектировании автомобилей используются геометрические тела для оптимизации обтекаемости, аэродинамики и прочности конструкции.

В науке геометрические тела применяются для моделирования и исследования различных физических явлений. Например, в физике геометрические тела используются для изучения тепловых процессов, взаимодействия света с веществом и других явлений.

Также геометрические тела находят применение в компьютерной графике и визуализации данных. Использование геометрических тел позволяет создавать реалистичные и детализированные изображения, а также эффективно представлять и анализировать различные виды данных.

Область применения	Примеры
Архитектура и строительство	Здания, мосты, туннели
Машиностроение	Автомобили, самолеты, суда
Наука	Физика, химия, биология
Компьютерная графика	Игры, анимация, визуализация данных

Группа геометрических тел в математике

В математике существует множество геометрических тел, которые можно классифицировать и объединять в различные группы. Эти тела обладают определенными свойствами и характеристиками, которые мы можем изучать и анализировать.

Одной из групп геометрических тел являются многогранники, или полиэдры. Они представляют собой трехмерные фигуры, ограниченные плоскими геометрическими фигурами, называемыми гранями. Многогранники могут быть правильными, когда все их грани равны и углы между ними одинаковы, или неправильными, когда грани различаются по форме и размерам.

Круглые тела, такие как сферы, цилиндры и конусы, также входят в группу геометрических тел. Они имеют форму, близкую к окружностям, и обладают особыми свойствами, такими как радиус, диаметр и высота.

Также в группу геометрических тел можно включить плоские фигуры, такие как треугольники, прямоугольники, квадраты и окружности. Хотя они не являются трехмерными, они все же имеют геометрические формы и характеристики, которые можно изучать и анализировать.

Все эти группы геометрических тел в математике имеют свои особенности и применения. Изучение и понимание этих тел помогает нам лучше разбираться в пространстве и формах, а также находить применение в различных областях науки и техники.

Что такое сторона в геометрии 8 класс?

В геометрии сторона — это одна из линий, образующих геометрическую фигуру. Она представляет собой отрезок, соединяющий две вершины фигуры.

Строить геометрические фигуры без использования сторон невозможно, поэтому понимание понятия «сторона» важно для изучения геометрии. В основе геометрии лежит понятие «геометрическая фигура», которая образуется отрезками и имеет определенную форму

В основе геометрии лежит понятие «геометрическая фигура», которая образуется отрезками и имеет определенную форму.

В зависимости от геометрической фигуры, сторона может иметь различные названия:

• В треугольнике стороны называются сторонами треугольника.
• В квадрате стороны называются сторонами квадрата.
• В прямоугольнике стороны называются сторонами прямоугольника.
• В параллелограмме стороны называются сторонами параллелограмма.
• И так далее для других геометрических фигур.

Строение геометрических фигур и их свойства определяются сторонами, поэтому понимание понятия «сторона» в геометрии является основополагающим для дальнейшего изучения этой науки.

Площадь и периметр

Площадь и периметр — это две основные характеристики геометрических фигур, которые позволяют определить их размеры и свойства.

Площадь — это мера двумерной площади, занимаемой фигурой на плоскости. Площадь обычно измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и т.д.).

Площадь различных геометрических фигур рассчитывается по-разному:

• Площадь прямоугольника равна произведению длины и ширины: S = a * b, где a и b — длина и ширина соответственно.
• Площадь квадрата равна квадрату его стороны: S = a^2, где a — длина стороны.
• Площадь треугольника может быть рассчитана различными способами, например, по формуле Герона или по формуле «основание на высоту делить на 2».
• Площадь круга равна произведению квадрата радиуса на число Пи: S = π * r^2, где r — радиус круга.

Периметр — это сумма всех сторон фигуры. Периметр также измеряется в единицах длины (метрах, сантиметрах и т.д.).

Периметр различных геометрических фигур рассчитывается по-разному:

• Периметр прямоугольника равен удвоенной сумме длины и ширины: P = 2 * (a + b), где a и b — длина и ширина соответственно.
• Периметр квадрата равен учетверенной длине его стороны: P = 4 * a, где a — длина стороны.
• Периметр треугольника равен сумме длин всех его сторон.
• Периметр круга равен произведению диаметра на число Пи: P = 2 * π * r, где r — радиус круга.

Знание формул для расчета площади и периметра помогает решать задачи на построение и нахождение размеров различных фигур.

Стороны и гипотенуза: теорема Пифагора

Теорема Пифагора — основополагающая теорема геометрии, которая устанавливает связь между длинами сторон прямоугольного треугольника. Согласно этой теореме, квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов.

Для обозначений длин сторон прямоугольного треугольника используют буквы a, b и c. Соответственно, гипотенуза обозначается буквой c, а каждый из катетов — буквой a или b.

Формула теоремы Пифагора выглядит следующим образом:

c2 = a2 + b2

Эта формула позволяет рассчитать длину гипотенузы, если известны длины катетов, или наоборот — длину одного из катетов, если известны длины гипотенузы и другого катета.

Применение теоремы Пифагора широко распространено в геометрии, физике, астрономии и других областях науки. К примеру, на основе этой теоремы можно рассчитать длину телескопической антенны, определить расстояние между звездами или найти длину диагонали экрана телевизора.

Какие еще методы могут использоваться для нахождения площади основания

В дополнение к классическим методам нахождения площади основания, есть и другие варианты, которые могут быть полезны в определенных ситуациях.

1. Использование геометрических фигур

Если форма основания не является прямоугольной или квадратной, можно разбить ее на более простые геометрические фигуры (например, треугольники, трапеции или круги). На основе этого можно найти площадь каждой фигуры и сложить их, чтобы получить общую площадь основания.

2. Использование метода Монте-Карло

Этот метод заключается в размещении точек на поверхности основания и подсчете количества точек, попавших внутрь фигуры основания. На основе этого можно определить отношение площади фигуры к площади общей поверхности. Чем больше точек используется, тем более точным становится результат.

3. Использование сканирующего лазера

Сканирующий лазер может использоваться для получения точных показаний размеров объекта, включая площадь основания. При этом нет необходимости делать сложные измерения вручную – все данные записываются автоматически в компьютер.

Вопрос-ответ

Вопрос: Как найти площадь основания прямоугольника?

Ответ: Площадь основания прямоугольника вычисляется как произведение его двух сторон.

Вопрос: Как найти площадь основания треугольника, если известны все его стороны?

Ответ: Площадь основания треугольника можно вычислить, используя формулу Герона: S = √p(p-a)(p-b)(p-c), где p – полупериметр треугольника, a, b и c – его стороны.

Вопрос: Как найти площадь основания круга?

Ответ: Площадь основания круга вычисляется по формуле S = πr², где r – радиус круга, π – математическая константа, примерно равная 3,14.

Вопрос: Как найти площадь основания призмы?

Ответ: Площадь основания призмы можно найти, зная форму основания. Например, для призмы с прямоугольным основанием площадь основания вычисляется как произведение его двух сторон.

Вопрос: Как найти площадь основания правильной треугольной пирамиды, если известна ее высота?

Ответ: Площадь основания правильной треугольной пирамиды можно найти, используя следующую формулу: S = (a²√3)/4, где a – длина стороны правильного треугольника, основания пирамиды. Затем умножаем полученную площадь на высоту пирамиды.

Главная — Советы — Простой и эффективный способ: как быстро найти площадь основания

Комментарии

Анна

5.0 out of 5.0 stars5.0

Екатерина
5.0 out of 5.0 stars5.0

Я всегда сталкиваюсь с проблемой вычисления площади основания объектов. Статья помогла мне разобраться в этом вопросе. Хорошо, что применение формулы и процесс вычисления расписаны по шагам, что облегчило мне задачу.

Ольга Смирнова
5.0 out of 5.0 stars5.0

Статья очень краткая и понятная. Теперь я знаю, как найти площадь основания. Спасибо!

Sapphire
5.0 out of 5.0 stars5.0

Как женщина, я часто оказываюсь в ситуации, когда нужно рассчитать площадь основания различных фигур — будь то круг, прямоугольник или треугольник. К сожалению, мои знания по математике и геометрии ограничены, и я не знаю, как найти площадь основания. Поэтому я рада, что наткнулась на эту статью. Статья помогла мне понять, что не нужно бояться главной формулы для рассчета площади основания — независимо от того, какая фигура у вас есть перед глазами. Все описано очень доступно и понятно. Я прочитала эту статью несколько раз, чтобы убедиться, что я точно понимаю, как найти площадь основания. Используя эту информацию, я смогла рассчитать площадь основания для нескольких примеров. Теперь у меня есть более четкое понимание того, что такое площадь основания, как ее рассчитывать и как это применять на практике. Большое спасибо за эту статью! Я уверена, что многие женщины, так же как и я, оценят ее доступность и понятность.

Елена Кузнецова
5.0 out of 5.0 stars5.0

Я уже давно хотела научиться находить площадь основания, но всегда боялась, что это сложно. Статья помогла мне понять, что это проще, чем кажется. Все описано доступно и понятно. Теперь я готова рассчитывать площадь оснований и делать это правильно!

Luna
5.0 out of 5.0 stars5.0

Статья понятная и полезная для решения задач по геометрии.

Свойства

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2

Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a

Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4

Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α

Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )

Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)

Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2

Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 )

Основание: определение и роль

Основание имеет ключевое значение в строительстве, инженерии и архитектуре. Оно обеспечивает стабильность и прочность всего сооружения. От качества основания зависит безопасность и долговечность строительных объектов.

Основное назначение основания — перераспределение нагрузки, которую оно получает от сверху на всю подстилающую площадку. Опоры и фундаменты передают нагрузку на основание, и если оно недостаточно крепкое или неравномерное, это может привести к деформации или разрушению сооружения.

Важно отметить, что несущая способность основания должна быть достаточной для поддержки всех нагрузок, включая вес сооружения, окружающие нагрузки (ветер, снег и т.д.) и динамические нагрузки (вибрация, землетрясение и т.д.). При проектировании зданий и сооружений необходимо тщательно анализировать и оценивать свойства основания, включая его геологическую структуру, грунтовую воду, устойчивость к деформациям и многие другие факторы

Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных

При проектировании зданий и сооружений необходимо тщательно анализировать и оценивать свойства основания, включая его геологическую структуру, грунтовую воду, устойчивость к деформациям и многие другие факторы. Выбор и расчет соответствующего фундамента или поддерживающей структуры зависит от таких данных.

Кроме того, при проведении строительных работ важно учесть возможные изменения основания в течение времени — например, связанные с периодическими повышениями уровня грунтовых вод или сезонными изменениями грунта

Основные геометрические фигуры

Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости. 

Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.

А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.

Разберём плоские фигуры.

Треугольник

Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.

 Есть три вида треугольников:

• Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
• Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
• Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.

Треугольники имеют следующие свойства:

• в треугольнике напротив большего угла лежит большая сторона и наоборот;
• сумма углов треугольника всегда равна 180 градусам;
• все углы равностороннего треугольника равны 60 градусам;
• в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.

Примеры треугольников:

Окружность

Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии. 

Круг

Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.

Прямоугольник

‍Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:

• противоположные стороны равны между собой;
• диагонали равны и делятся в точке пересечения пополам;
• около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.

Квадрат

Квадрат — это тот же прямоугольник, у которого:

• все стороны равны;
• все углы равны и составляют 90 градусов;
• диагонали равны и перпендикулярны;
• центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.

Трапеция

Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность. 

Параллелограмм и ромб

Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.

Ромб — это параллелограмм с равными сторонами.

Параллелограмм имеет следующие свойства:

• противоположные стороны и углы равны;
• сумма двух любых соседних углов равна 180 градусам;
• диагонали пересекаются и точкой пересечения делятся пополам;
• каждая диагональ делит фигуру на два равных треугольника.

Свойства равнобедренного треугольника

Свойство первое

В равнобедренном треугольнике углы основания равны.

Внимание. Если преподаватель обнаружит плагиат в вашей работе, вам не избежать серьезных проблем (вплоть до выкидыша)

Если вы не можете написать работу самостоятельно, закажите ее здесь.

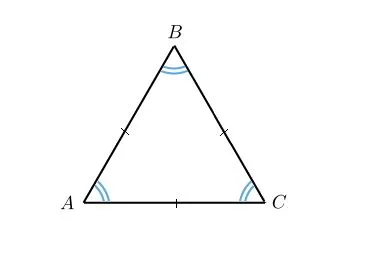
Дана равнобедренная фигура DABC, где ab = ac. В ее основании находится дикатор ad.

Поскольку каждый AD является бисекторальным, угол ¶1 равен углу ρ2. Рекламная часть является общей для DADB и DADC. Поэтому она равна первой функции. Далее, угол ∠B равен углу amc.

Свойство второе

В равнобедренных треугольниках биссектрисы, падающие на основание, являются медианой и высотой.

Дана равнобедренная фигура DABC, где ab = ac. В ее основании находится дикатор ad.

Поскольку каждый AD является биссектрисой, угол ¶1 равен углу ρ2. Рекламная часть является общей для DADB и DADC. Тогда эти треугольники равны первому знаку. Тогда bd = dc. Следовательно, AD — медиана.

Сумма углов треугольников равна 180°, то есть am a + am b +∠C = 180°. Угол am a = 2*¶1, так как ad — биссектриса.

dACD∠CDA +∠1 +∠2= 180°, поэтому ¶cda = 90°.

Свойство третье

В изоширном треугольнике интерстиции, спроектированные вершиной основания (соответственно, высота и лучшая из них) равны.

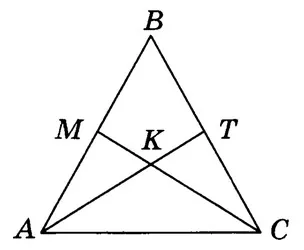
ab = ac.

Поскольку AT и MC — биссектрисы равных углов, ∠BAT = ∠BCM. ∠B является общим для ΔABT и ΔCBM. Поэтому ΔABT и ΔCBM равны со вторым знаком. Далее, AT=CM.

Что такое основание трапеции?

Основание трапеции является одним из важных параметров, влияющих на ее площадь и другие характеристики. Он определяет ширину трапеции и ее расстояние от вершин до основания. Зная высоту и одно из оснований трапеции, можно вычислить другое основание и другие параметры фигуры.

Что такое высота трапеции?

Высота трапеции имеет свойство разделять ее на два треугольника: один, который состоит из одной из сторон трапеции и ее основания, и другой, состоящий из второй стороны и основания

Обратите внимание, что оба треугольника имеют общую высоту — это высота трапеции

Высота трапеции является важным понятием при вычислении площади и других параметров трапеции. Зная значение высоты и одну из оснований, можно вычислить второе основание, а также площадь трапеции. Высота также помогает определить острый угол и высоты внутренних треугольников.

Пример:

Пусть дана трапеция ABCD, где AB и CD — основания, а H — высота. Известно, что основания равны AB = 10 см и CD = 6 см, а высота H = 8 см. Чтобы найти оставшийся параметр, воспользуемся формулой для площади трапеции: S = (AB + CD) * H / 2.

Подставляя значения, получаем S = (10 + 6) * 8 / 2 = 16 * 8 / 2 = 16 * 4 = 64 см². Таким образом, площадь этой трапеции равна 64 квадратным сантиметрам.

Как найти основание трапеции через высоту и основание?

Для нахождения основания трапеции через высоту и одно из оснований, нам нужно знать формулу для нахождения площади трапеции. Формула для площади трапеции состоит из умножения полусуммы оснований на высоту трапеции:

S = (a + b) * h / 2,

где S — площадь трапеции, a и b — основания трапеции, h — высота трапеции.

Таким образом, чтобы найти одно из оснований трапеции, нужно знать площадь, высоту и другое основание. Подставив известные значения в формулу для площади, можно найти нужное основание, перегруппировав уравнение:

a = (2 * S — b * h) / h.

Применим эти знания на примере. Предположим, у нас есть трапеция с площадью 36 квадратных сантиметров, высотой 8 сантиметров и основанием 12 сантиметров. Чтобы найти другое основание, используем формулу:

a = (2 * 36 — 12 * / 8 = 36 / 8 = 4.5.

Таким образом, другое основание этой трапеции равно 4.5 сантиметра.

Простое объяснение с примером

Высота трапеции — это отрезок, который соединяет две параллельные стороны и перпендикулярен им. Чтобы найти основание трапеции, используем следующую формулу:

Основание = 2 * (площадь трапеции) / (высота)

Возьмем пример. Представим, что у нас есть трапеция с высотой 10 единиц и площадью 60 квадратных единиц. Чтобы найти основание, мы используем формулу:

Основание = 2 * (площадь) / (высота)

Основание = 2 * 60 / 10

Основание = 12

Таким образом, основание трапеции равно 12 единицам.

Дополнительные примеры нахождения основания трапеции через высоту и основание

При решении задач на нахождение основания трапеции по высоте и одной из оснований можно использовать формулу для расчета площади трапеции:

S = (a + b) * h / 2

где a и b – основания трапеции, h – высота трапеции.

Найдем значение одного из оснований, используя данную формулу и известные значения высоты и другого основания.

1. Пример 1:

   Дано: высота трапеции h = 6 см, основание a = 10 см.

   Необходимо найти значение основания b.

   Для решения задачи используем формулу:

   S = (a + b) * h / 2

   Подставляем известные значения:

   S = (10 + b) * 6 / 2

   Решаем уравнение:

   60 = 3b

   b = 20 см

   Ответ: основание трапеции b = 20 см.

2. Пример 2:

   Дано: высота трапеции h = 8 м, основание b = 15 м.

   Необходимо найти значение основания a.

   Для решения задачи используем формулу:

   S = (a + b) * h / 2

   Подставляем известные значения:

   S = (a + 15) * 8 / 2

   Решаем уравнение:

   S = 4a + 60

   a = (S — 60) / 4

   Ответ: основание трапеции a = (S — 60) / 4.

Таким образом, зная высоту и одно из оснований трапеции, можно легко найти значение другого основания, используя формулу для расчета площади.

Что должен знать ребенок о геометрических фигурах

Важно: Геометрические фигуры — общепринятые эталоны, меры измерения формы предметов. Поэтому домашнее ознакомление ребенка с формами должно проходить не отдельно, а в системе сенсорного (чувственного) воспитания. Лучше всего кроха запомнит форму, когда параллельно рассматривает цвет, величину, назначение предмета, так как в разнообразной деятельности знания активно используются и лучше запоминаются

Лучше всего кроха запомнит форму, когда параллельно рассматривает цвет, величину, назначение предмета, так как в разнообразной деятельности знания активно используются и лучше запоминаются.

1. Специалисты утверждают, что целенаправленно обучать ребенка геометрическим фигурам в домашних условиях надо начинать на третьем году жизни. В это время у деток появляется двигательный и осязательный опыт изучения окружающего мира. Они умеют говорить, отличаются любознательностью и желанием все исследовать, стремятся к новому. Именно поэтому для дальнейшего формирования знаний у детей нужна работа в пополнении представлений о геометрических фигурах: круге, квадрате, треугольнике. В увлекательной игре (не специально!) кроха знакомится с шариком (шар), кубиком (куб).
2. Четырех — пятилетние детки кроме треугольных, квадратных, круглых форм узнают прямоугольные и овальные. Считается, что в 5 лет дети уже осваивают геометрию, поэтому к следующему возрастному этапу они должны четко называть круг, овал, треугольник, квадрат, ромб, различать их и находить вокруг себя. Дошколята должны уметь анализировать и обобщать форму предметов, отмечая основные свойства, и даже решать логические задачи, сравнивая фигуры. Например, в популярной игре «Чем похожи и не похожи круг и квадрат, квадрат и прямоугольник, круг и овал?».
3. Старшие дошколята уже хорошо знают названия всех фигур, их знакомят с новыми: плоскостными (многоугольник, трапеция) и объемными (шар, куб, цилиндр и конус). Для школьного обучения детям нужно научиться делить и собирать фигуры разными способами (разрезанием и складыванием), решать задачи — головоломки, например, «Знаете ли вы, как составить из двух частей квадрат, прямоугольник, треугольник?», «Сколько квадратов (кругов, прямоугольников) на рисунке?».

Основание равностороннего треугольника: как найти?

Основание равностороннего треугольника — это любая из его сторон. Так как все три стороны равны, то можно выбрать любую из них в качестве основания.

Способы нахождения основания равностороннего треугольника могут быть различными:

• Нахождение по формуле для периметра треугольника: основание равностороннего треугольника равно периметру треугольника, поделенному на 3.
• Нахождение по высоте: высота равностороннего треугольника проходит через середину основания и перпендикулярна ему. Таким образом, если известна высота, то основание можно найти, удвоив её длину.
• Нахождение по углу: если известен угол между основанием и боковой стороной, то основание можно вычислить, используя формулу синуса, т. е. делением боковой стороны на синус угла.

Зная же длину одной стороны равностороннего треугольника, можно найти длину любой другой стороны, используя свойства равностороннего треугольника. Например, длина высоты, проведенной к любой из сторон, равна половине длины биссектрисы, проведенной из вершины, противоположной этой стороне.

Таким образом, для нахождения основания равностороннего треугольника доступно несколько способов, которые могут быть использованы в зависимости от известных данных.

Практические применения

Строительство:

Знание стороны основания является важным при строительстве зданий и сооружений. Оно позволяет правильно расчертить фундаменты, определить границы строительной площадки и разместить строительное оборудование. Точные измерения стороны основания помогают минимизировать ошибки и повышают качество строительных работ.

Геодезия:

Сторона основания находит свое применение в геодезических работах. Геодезисты используют этот параметр для определения координат точек на местности и создания картографических материалов. Например, при построении топографической карты или при установке геодезических меток, знание стороны основания позволяет правильно определить местоположение объекта.

Инженерные расчеты:

Сторона основания используется в инженерных расчетах для определения площади или объема геометрической фигуры. Например, при проектировании водоема или сборном бассейне, знание стороны основания позволяет правильно определить геометрию конструкции и сделать необходимые расчеты для ее создания.

Машиностроение:

В машиностроении сторона основания применяется для разработки и создания различных деталей и механизмов. Знание этого параметра помогает правильно вычислить размеры и пропорции детали, а также предотвратить возможные деформации или поломки в процессе эксплуатации.

Архитектура:

В архитектуре сторона основания является важным параметром при проектировании зданий и интерьеров. Она позволяет определить пропорции и размеры строения, а также расположение отдельных элементов. Знание этого параметра помогает создавать гармоничные и функциональные архитектурные решения.

Разработка программного обеспечения:

Сторона основания находит применение и в программировании. В разработке программного обеспечения этот параметр может использоваться для определения размеров окна, ширины и высоты интерфейсных элементов и многого другого. Он позволяет создавать пользовательские интерфейсы, которые комфортны для работы и удобны в использовании.