Виды векторов[править | править код]
Иногда вместо того, чтобы рассматривать в качестве векторов множество всех направленных отрезков (рассматривая как различные все направленные отрезки, начала и концы которых не совпадают), берут только некоторую модификацию этого множества (фактормножество), то есть, некоторые направленные отрезки рассматривают как равные, если они имеют одинаковое направление и длину, хотя они могут иметь разное начало (и конец), то есть направленные отрезки одинаковой длины и направления считаются представляющими один и тот же вектор; таким образом, каждому вектору оказывается соответствующим целый класс направленных отрезков, одинаковых по длине и направлению, но различающихся началом (и концом).
Так, говорят о «свободных», «скользящих» и «фиксированных» векторах. Эти виды отличаются понятием равенства двух векторов.
- Говоря о свободных векторах, отождествляют любые векторы, имеющие одинаковое направление и длину;
- говоря о скользящих векторах — добавляют, что начала равных скользящих векторов должны совпадать или лежать на одной прямой, на которой лежат изображающие эти векторы направленные отрезки (так что один может быть совмещен с другим перемещением в направлении, им же самим задаваемом);
- говоря о фиксированных векторах — говорят, что равными считаются только векторы, у которых совпадают и направления, и начала (то есть в этом случае факторизации нет: нет двух фиксированных векторов с различными началами, которые считались бы равными).
Формально:
Говорят, что свободные векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны, если найдутся точки E{\displaystyle E} и F{\displaystyle F} такие, что четырёхугольники ABFE{\displaystyle ABFE} и CDFE{\displaystyle CDFE} — параллелограммы.
Говорят, что скользящие векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны, если
- точки A,B,C,D{\displaystyle A,B,C,D} располагаются на одной прямой,
- векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны между собой как свободные векторы.
Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила, действующая на твердое тело. Перенос начала вектора силы вдоль прямой, на которой он лежит, не меняет момента силы относительно любой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (даже почти всегда вызовет): поэтому при вычислении момента нельзя рассматривать силу как свободный вектор, то есть, нельзя её считать приложенной к произвольной точке твердого тела.
Говорят, что фиксированные векторы AB→{\displaystyle {\overrightarrow {AB}}} и CD→{\displaystyle \ {\overrightarrow {CD}}} равны, если попарно совпадают точки A{\displaystyle A} и C{\displaystyle C}, B{\displaystyle B} и D{\displaystyle D}.
Вектором в одном случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Все операции над векторами (сложение, умножение на число, скалярное и векторное произведения, вычисление модуля или длины, угла между векторами и т. д.) в принципе определены одинаково для всех типов векторов, различие в типах сводится в этом отношении только к тому, что для скользящих и фиксированных наложено ограничение на возможность осуществления операций между двумя векторами, имеющими разное начало (так, для двух фиксированных векторов запрещено — или лишено смысла — сложение, если их начала отличаются; однако для всех случаев, когда эта операция разрешена — или имеет смысл — она такова же, как для свободных векторов). Поэтому часто тип вектора вообще явно не указывается, подразумевается, что он очевиден из контекста. Более того, один и тот же вектор в зависимости от контекста задачи может рассматриваться как фиксированный, скользящий или свободный, например, в механике векторы сил, приложенных к телу, могут суммироваться независимо от точки приложения при нахождении равнодействующей (и в статике, и в динамике при исследовании движения центра масс, изменения импульса и т. п.), но не могут складываться друг с другом без учета точек приложения при вычислении вращающего момента (также и в статике и в динамике).
Координаты векторов
Из курса алгебры нам известна прямоугольная система координат. В ней есть оси Ох и Оу, а каждая отмеченная на плоскости точка имеет свои координаты:
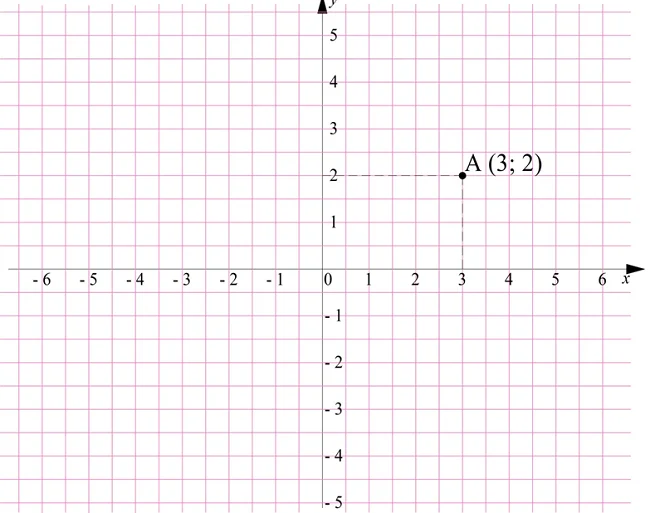
Естественно, что на координатной плоскости можно отметить и вектора. Построим два вектора, которые начинаются в начале координат, имеют длину, равную единице, и направление которых совпадает с направлениями осей координат. Тот вектор, который лежит на оси Ох, обозначают буквой i, а тот, который лежит на оси Оу, обозначают как j.
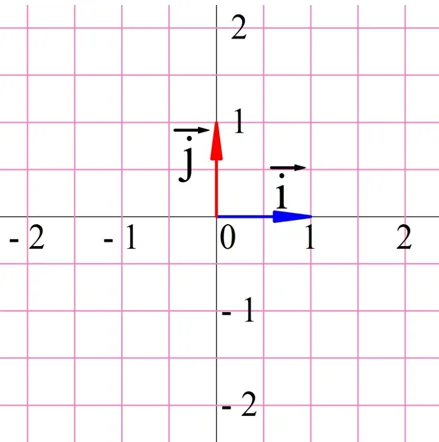
Эти вектора называют единичными векторами, или ортами (ещё используется термин координатный вектор). Они не коллинеарны друг другу, а это означает, что любой вектор на плоскости можно разложить на единичные вектора. Коэффициенты такого разложения как раз и являются координатами вектора.
Посмотрим на примере, как находить координаты вектора. Пусть задан вектор а:
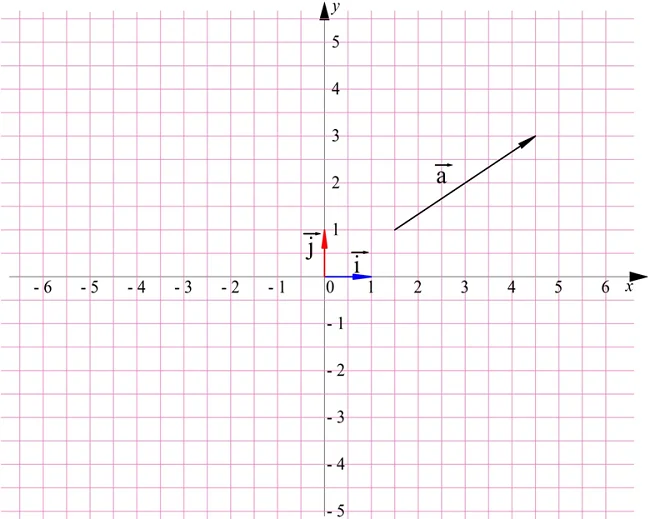
Нам надо разложить а по векторам i и j. Для этого их следует отложить от одной точки. Удобно перенести вектор а к началу координат:
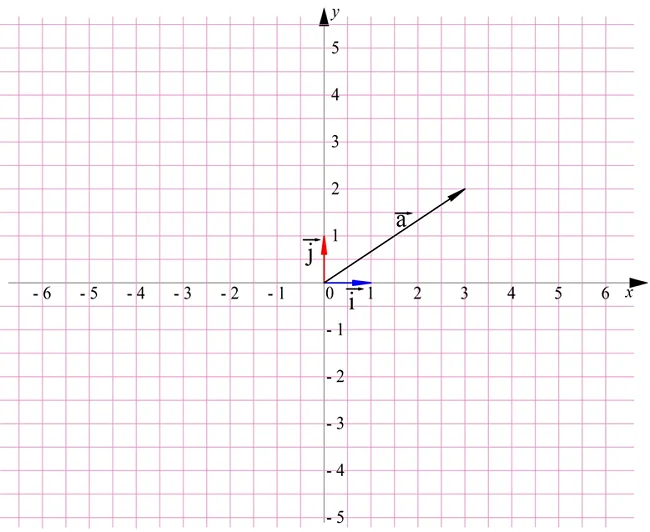
Теперь надо через конец а провести прямые, параллельные векторам iи j. В результате получится прямоугольник АВСD:
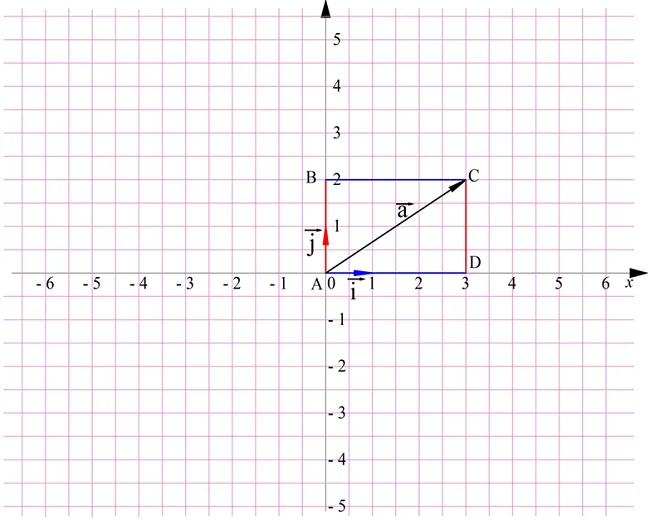
Можно записать равенство:
Значит, и координаты данного вектора – это числа 3 и 2. Записывается это так:
Обратите внимание, что порядок чисел в скобках принципиально важен. Первое число – это коэффициент разложения, стоящий перед вектором i
Эту координату можно называть координатой х (по аналогии с координатами точек). Второе число – это коэффициент при векторе j, оно является координатой у. Также заметим очевидный факт, что координаты равных векторов одинаковы.
В приведенном выше примере легко заметить, что после того, как мы перенесли вектор в начало координат, координаты его конца (он обозначен точкой С) совпали с координатами самого вектора. Действительно, точка С имеет координаты (3; 2).
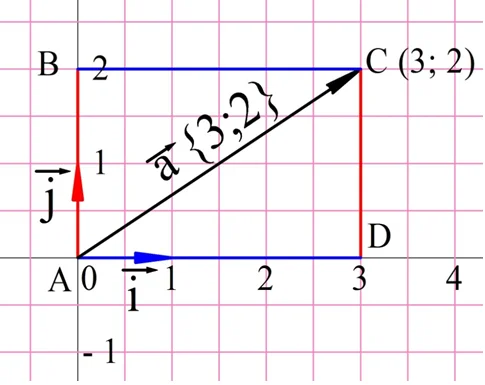
Это правильно несколько упрощает определение координат вектора. Достаточно просто отложить вектор от точки начала координат, после чего посмотреть на координаты его конечной точки. Отметим, что вектор, чье начало совпадает с началом координат, имеет особое название – радиус-вектор.
Задание. Определите координаты векторов a, b, c и d, отмеченных на рисунке:
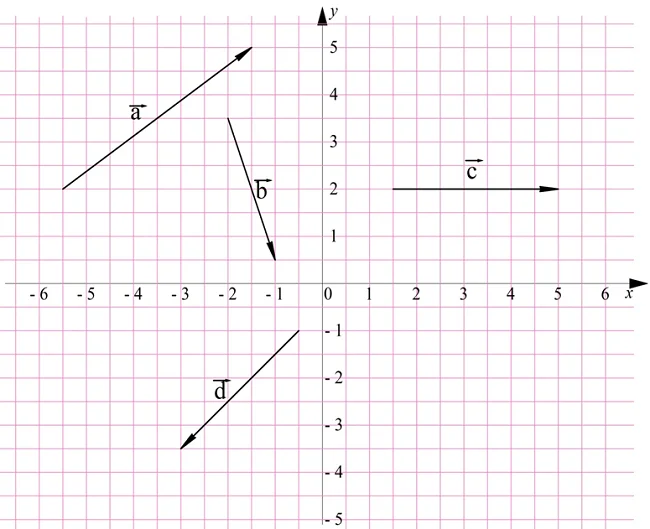
Решение. Во всех случаях будем просто переносить вектора к началу координат, получая радиус вектора. Далее будем просто смотреть, каковы координаты конца радиус-вектора. Начнем с а:
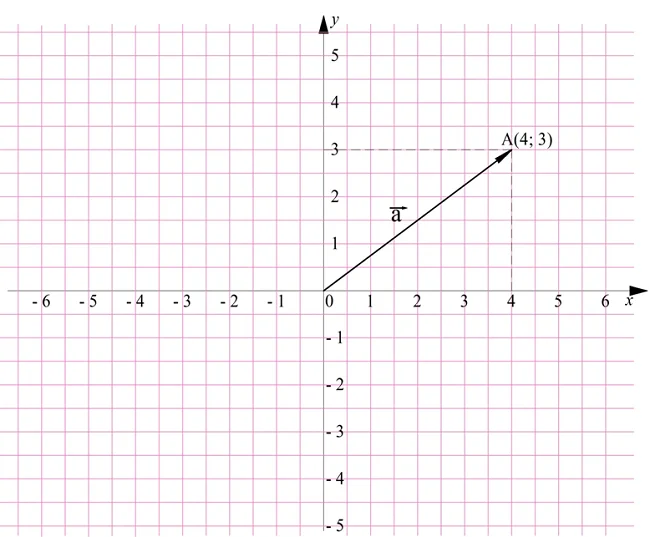
После переноса а его конец оказался в точке А(4; 3), поэтому и координаты всего вектора можно записать так:
После переноса вершина радиус-вектора попала в точку B (1; – 3), поэтому вектор имеет координаты {1; – 3}.
Выполним построение и для с:
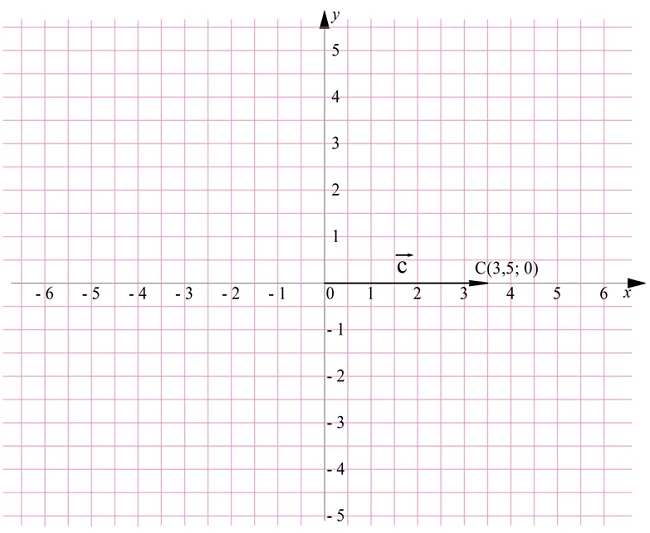
Конец вектора попал в точку С (3,5; 0), а потому и координаты вектора составляют {3,5; 0}.
Осталось рассмотреть d:
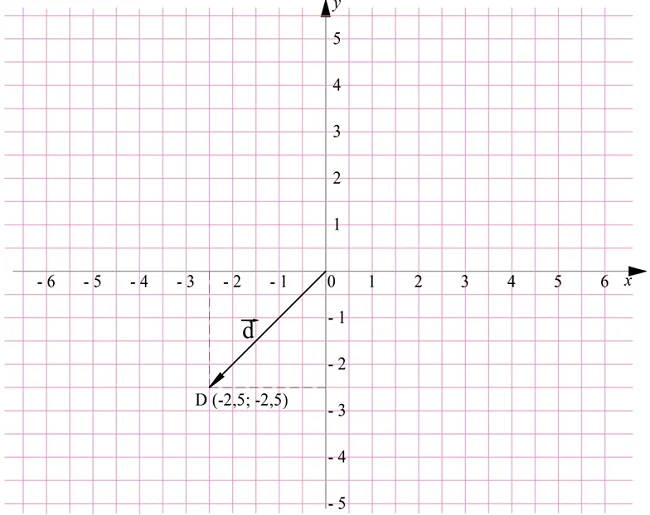
Здесь координаты вектора будут равны {– 2,5; – 2,5}, так как такие же координаты имеет точка D.
Ответ: а{4;3}; b{1; – 3}; с{3,5; 0}; d{– 2,5; – 2,5}.
Рассмотрим решение обратной задачи, в которой необходимо построить вектор по заранее заданным координатам.
Задание. Даны координаты вектора:
Постройте по три вектора, имеющие заданные координаты.
Решение. Проще всего построить радиус-вектор, вершина которого будет иметь те же координаты, что и требуемый вектор:
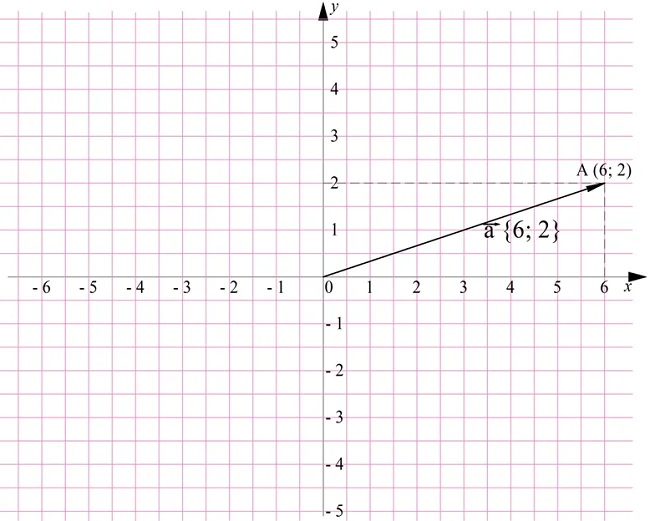
Чтобы построить ещё два вектора с такими же координатами, надо просто отложить уже построенный вектор от любых других точек:
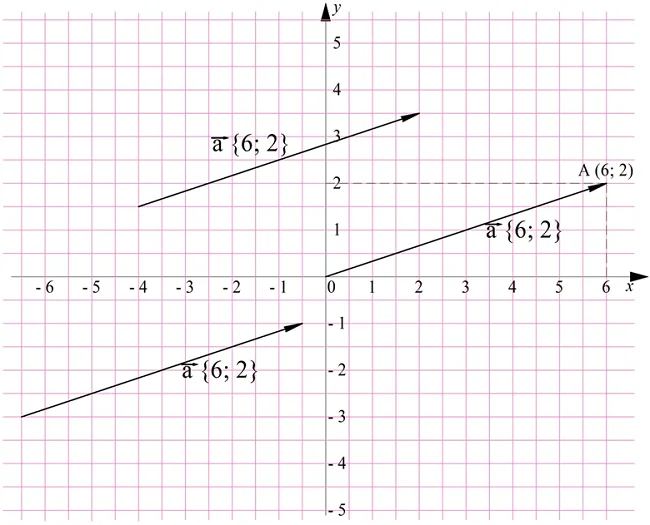
Аналогично поступаем и во второй задаче – сначала откладываем радиус-вектор с заданными координатами, а потом добавляем ещё два равных ему вектора, отложенных от других точек:
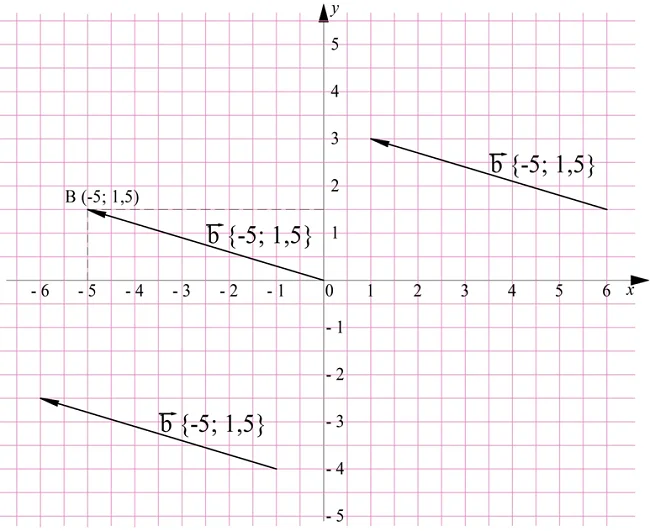
Отдельно отметим нулевой вектор. Очевидно, что все его координаты равны нулю, так как для него можно записать такое разложение на орты:
Также можно сказать, что если отложить нулевой вектор от начала координат, то его конец также будет находиться в начале координат (так как у нулевого вектора начало и конец совпадают), то есть в точке с координатами (0; 0).
12 Координаты вектора в пространстве
Что такое вектор
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.
Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.
Аналитическое представление вектора: данные можно перевести в числа
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.
Математическое представление вектора: данные можно перевести в числа или график
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.
Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат
Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.
Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.
Что такое координаты вектора
Вектором называют некое направление в виде отрезка с определенными в пространстве начальной и конечной точками.
Предусмотрено стандартизированное обозначение вектора. К примеру, если в точке А какой-то вектор берет свое начало, а в точке В — заканчивается, то его записывают таким образом: \(\overrightarrow{AB}\). Допустимо использовать и сокращенный вариант, к примеру: \(\overrightarrow{a}\).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут
В некоторых случаях уместно сформулировать понятие вектора как передвижение из начальной точки А в конечную точку В. Согласно ранее записанному определению, вектор характеризуется некой длиной. К примеру, для \(\overrightarrow{AB}\) длиной, либо модулем, является протяженность отрезка АВ. Данное утверждение допустимо сформулировать в виде математического соотношения:
\(|\overrightarrow{AB}|=AB\)
Примечание 1
Заметим, что не исключены случаи совпадения начальной и конечной точек рассматриваемого вектора. Тогда говорят, что этот вектор является нулевым.
Школьникам и студентам часто приходится иметь дело с векторами. С таким понятием нередко встречаются учащиеся в процессе решения контрольных и самостоятельных работ по геометрии и физике. Как правило, рассматривается декартова координатная система, ориентируясь на которую можно вычислить координаты соответствующего отрезка с конкретным направлением. Процедура заключается в разложении заданного направленного отрезка по базисным векторам.
Принцип основан на фундаментальных знаниях геометрии. В результате получается интерпретировать это действие в виде векторной проекции относительно осей координат. При наличии данных о координатах, которым соответствуют точки начала и конца вектора, представляется возможным рассчитать непосредственно координаты искомого вектора. Процедура подразумевает расчет разности между координатами точки, где вектор заканчивается, и координатами точки, в которой он начинается.
Рассматриваемое действие по идентификации координат вектора целесообразно записать в общей форме таким образом:
\(\overrightarrow {AB}=(AB_{x},AB_{y},AB_{z})=(B_{x}-A_{x},B_{y}-A_{y},B_{z}-A_{z})\)
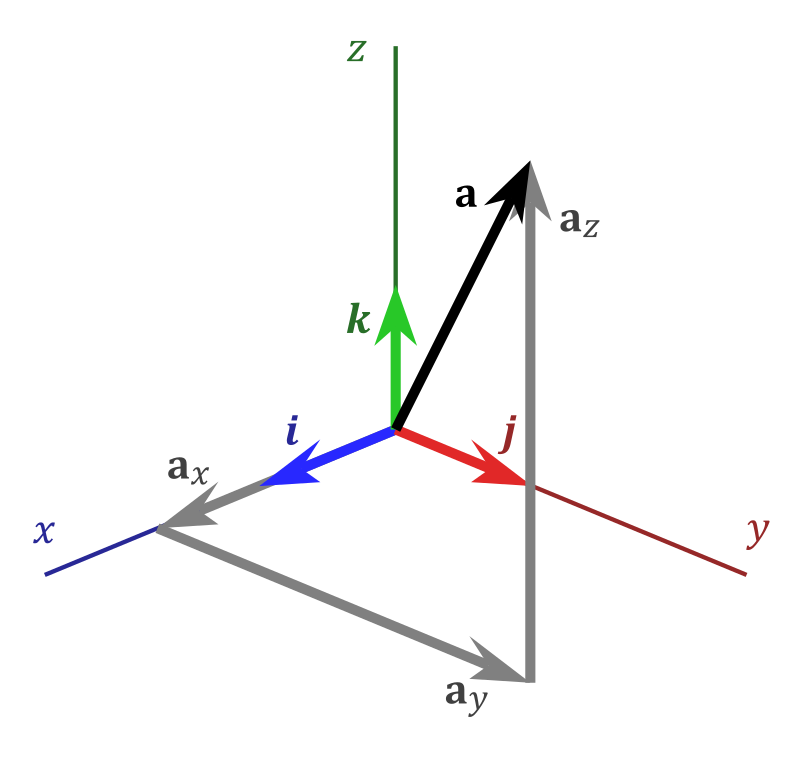
В качестве базиса принято рассматривать орты координат. Для их обозначения используют \({\vec {k}}{\vec {i}},{\vec {j}},{\vec {k}}\), которые соответствуют осям x,y,z. При таких условиях \({\vec {a}}\) допустимо выразить с помощью следующего математического соотношения:
\({\vec {a}}=a_{x}{\vec {i}}+a_{y}{\vec {j}}+a_{z}{\vec {k}}\)
Заметим, что какое-либо свойство в науке геометрии допустимо сформулировать с помощью координат. В результате оно приобретает алгебраическую форму, что позволяет значительно упростить решение тех или иных задач. С другой стороны, несколько некорректно применять обратный принцип действий.
Координаты вектора представляют собой проекции х и у заданного вектора \(\overrightarrow {AB}\) на координатные оси в рамках прямоугольной координатной системы.
В решении задач уже привычно использовать различные закономерности, с помощью которых можно значительно упростить вычисления. В ходе изучения темы координат вектора можно также выделить несколько полезных признаков. Перечислим свойства направленных отрезков:
- В рамках общей координатной системы какие-либо векторы, которые идентичны друг другу, обладают аналогичными координатами.
- Если вектора являются коллинеарными, то их координаты пропорциональны. При этом рассматриваемые вектора не должны обладать нулевым значением.
- Протяженность произвольного вектора во второй степени соответствует результату сложения координат данного вектора, возведенных во вторую степень.
- Произведение некого вектора и числа из множества действительных подразумевает произведение каждой из координат заданного вектора на это число.
- Если требуется суммировать вектора, то следует сложить их координаты.
- Вычисление скалярного произведения пары векторов заключается в сложении произведений координат, которые принадлежат рассматриваемым векторам.
Как изображать
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.
Графическое представление скаляра. Записывается в круглых скобках
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.
Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.
Графическое представление числового вектора в двух измерениях
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.
Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.
Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4
Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке
Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства
Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.
Как найти координаты вектора: формулы
Зная координаты вектора, можно производить с ними разнообразные вычисления. Справедливо и обратное, то есть при известных характеристиках вектора допустимо рассчитать, чему равны его координаты. Рассмотрим ряд полезных соотношений, которые значительно упростят процесс решения заданий на поиск координаты векторов. Начнем с простейшего выражения, позволяющего достаточно быстро определить координаты вектора при известных идентификаторах точек начала и конца:
\(\overline{AB}=\left(x_{2} -x_{1} ;\; y_{2} -y_{1} \right)\)
\(\overline{AB}=\left(b_{1} -a_{1} ;\; b_{2} -a_{2} ;\; b_{3} -a_{3} \right)\)
Пример 1
В качестве примера рассмотрим некий вектор \(\overline{AB}\). Пусть этот вектор начинается в точке \(A\left(3;\; -1\right)\), а заканчивается в точке \(B\left(0;\; 2\right)\). Попробуем вычислить, чему равны координаты такого вектора.
Воспользуемся уже знакомым математическим выражением и найдем ответ к этой задаче:
\(\overline{AB}=\left(0-3;\; 2-\left(-1\right)\right)=\left(-3;\; 3\right)\)
Таким образом:
\(\overline{AB}=\left(-3;\; 3\right)\)
Координаты вектора можно использовать при вычислении протяженности направленного отрезка. Представим, что имеется некий вектор \(\bar{a}=\left(a_{1} ;\; a_{2} ;\; a_{3} \right)\)В таком случае справедливым является следующее равенство:
\(\left|\bar{a}\right|=\sqrt{a_{1}^{2} +a_{2}^{2} +a_{2}^{3} }\)
Заметим, что данное соотношение допустимо использовать и тогда, когда требуется рассчитать координаты направленного отрезка.
Пример 2
Попробуем определить, чему равен модуль направленного отрезка, записанного с помощью простого выражения: \(\bar{a}=\left(3;\; 4\right)\)
Воспользуемся ранее изученной формулой, с помощью которой не составит труда определить искомую величину:
\(\left|\bar{a}\right|=\sqrt{3^{2} +4^{2} } =\sqrt{9+16} =\sqrt{25} =5\)
Таким образом:
\(\left|\bar{a}\right|=5\)
Другим вариантом применения координат направленного отрезка является вычисления угла, который расположен между парой векторов. В данном случае целесообразно воспользоваться следующим справедливым равенством:
\(\cos \varphi =\frac{\left(\bar{a},\; \bar{b}\right)}{\left|\bar{a}\right|\cdot \left|\bar{b}\right|}\)
С целью лучше разобраться в таком достаточно сложном соотношении величин попробуем решить типичный пример. Это поможет наглядно продемонстрировать применение уравнения на практике.
Пример 3
Предположим, что пара произвольных векторов задана следующими координатами: \(\bar{a}=\left(1;\; 1\right) \bar{b}=\left(0;\; 1\right)\) Исходя из условий, требуется вычислить угол, расположенный между этими направленными отрезками.
Запишем выражение для расчета косинуса искомого угла:
\(\cos \varphi =\frac{\left(\bar{a},\; \bar{b}\right)}{\left|\bar{a}\right|\cdot \left|\bar{b}\right|} \Rightarrow \varphi =\arccos \frac{\left(\bar{a},\; \bar{b}\right)}{\left|\bar{a}\right|\cdot \left|\bar{b}\right|}\)
В результате получим следующее соотношение:
\(\varphi =\arccos \frac{1\cdot 0+1\cdot 1}{\sqrt{1^{2} +1^{2} } \cdot \sqrt{0^{2} +1^{2} } } =\arccos \frac{0+1}{\sqrt{1+1} \cdot \sqrt{0+1} } =\arccos \frac{1}{\sqrt{2} } = \arccos \frac{\sqrt{2} }{2} =\frac{\pi }{4}\)
Таким образом:
\(\varphi =\frac{\pi }{4}\)
Подробное объяснение процесса построения вектора
Для построения вектора по трем координатам необходимо выполнить следующие шаги:
- Определить начальную точку в координатной системе. Начало координат обозначается точкой O.
- Используя первую координату, перемещаемся по оси X вправо (в положительном направлении), если координата положительна, или влево (в отрицательном направлении), если координата отрицательна. Точка, в которую мы попадём, будет одной из точек нашего вектора.
- От полученной точки выпускаем перпендикуляр на ось OX. Если вектор направлен вверх, перпендикуляр будет проходить над осью OX, а если вниз – под осью OX.
- С длиной, определенной по второй координате, откладываем от этой перпендикуляра отрезок вверх или вниз, в соответствии с положительным или отрицательным значением координаты. Заканчиваем отрезок в этой новой точке.
- Используя третью координату, перемещаемся по оси Z вверх (в положительном направлении), если координата положительна, или вниз (в отрицательном направлении), если координата отрицательна. Точка, полученная после этого перемещения, будет конечной точкой вектора.
Таким образом, мы можем построить вектор, заданный тремя координатами, в трехмерном пространстве. Направление и длина вектора будут определены значениями этих координат.
Пример:
- Пусть у нас есть вектор с координатами (2, -3, 1).
- Начинаем соединять точки O(0, 0, 0) и (2, 0, 0) из-за положительного значения первой координаты.
- Выпускаем перпендикуляр над осью OX.
- Откладываем от этой перпендикуляра отрезок вниз на 3 единицы, из-за отрицательного значения второй координаты.
- Перемещаемся по оси Z вверх на 1 единицу, из-за положительного значения третьей координаты, и получаем конечную точку вектора.
- Таким образом, вектор с координатами (2, -3, 1) будет представлен отрезком, идущим от точки O(0, 0, 0) к точке (2, -3, 1).
Базис.
Ранее было дано определение . Введем теперь определение базиса.
Определение.
Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства по ней раскладывается.
Из доказанной выше сразу вытекает, что
- В нулевом пространстве базиса не существует.
- В одномерном пространстве (на прямой линии) базис состоит из одного ненулевого вектора.
- В двумерном пространстве (на плоскости) базис — упорядоченная пара неколлинеарных векторов.
- В трехмерном пространстве базис — упорядоченная тройка некомпланарных векторов.
Требование упорядоченности означает, что, например, в случае плоскости \(\boldsymbol{a}\), \(\boldsymbol{b}\) и \(\boldsymbol{b}\), \(\boldsymbol{a}\) — два разных базиса.
Так как векторы базиса линейно независимы, коэффициенты разложения по базису для каждого вектора пространства определены однозначно. Они называются компонентами или координатами вектора в этом базисе.
Таким образом, если \(\boldsymbol{e_{1}}\), \(\boldsymbol{e_{2}}\), \(\boldsymbol{e_{3}}\) — базис трехмерного пространства, то по формуле \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) каждому вектору сопоставлена единственная упорядоченная тройка чисел \(\alpha_{1}\), \(\alpha_{2}\), \(\alpha_{3}\) и каждой тройке чисел — единственный вектор. Аналогично, вектор на плоскости имеет две компоненты, а на прямой — одну.
Компоненты пишутся в скобках после буквенного обозначения вектора, например \(\boldsymbol{a}\)(1,0,1).
В аналитической геометрии геометрические рассуждения о векторах сводятся к вычислениям, в которых участвуют компоненты этих векторов. Следующее предложение показывает, как производятся линейные операции над векторами, если известны их компоненты.
Утверждение 5.
При умножении вектора на число все его компоненты умножаются на это число. При сложении векторов складываются их соответствующие компоненты.
Действительно, если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\), то
$$
\lambda\boldsymbol{a} = \lambda(\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) = (\lambda\alpha_{1})\boldsymbol{e_{1}} + (\lambda\alpha_{2})\boldsymbol{e_{2}} + (\lambda\alpha_{3})\boldsymbol{e_{3}}.\nonumber
$$
Если \(\boldsymbol{a} = \alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}\) и \(\boldsymbol{b} = \beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}\), то
$$
\boldsymbol{a} + \boldsymbol{b} = (\alpha_{1}\boldsymbol{e_{1}} + \alpha_{2}\boldsymbol{e_{2}} + \alpha_{3}\boldsymbol{e_{3}}) + (\beta_{1}\boldsymbol{e_{1}} + \beta_{2}\boldsymbol{e_{2}} + \beta_{3}\boldsymbol{e_{3}}) =\\= (\alpha_{1} + \beta_{1})\boldsymbol{e_{1}} + (\alpha_{2} + \beta_{2})\boldsymbol{e_{2}} + (\alpha_{3} + \beta_{3})\boldsymbol{e_{3}}.\nonumber
$$
Для одномерного и двумерного пространств доказательство отличается только числом слагаемых.
Практика делает мастера!
Теперь, когда вы понимаете, как векторы могут быть полезными в различных областях, пришло время попрактиковаться. Постарайтесь применить свои знания о векторах в реальной жизни. Например, попробуйте построить вектор, указывающий на ближайший супермаркет от вашего дома или на направление, в котором вы хотите развиваться профессионально. Это поможет вам лучше осознать, как векторы работают и как их использование может сделать вашу жизнь более увлекательной и организованной.
Надеюсь, что эти практические примеры помогут вам лучше понять, как работать с векторами в различных областях. Не бойтесь экспериментировать и использовать векторы в своей повседневной жизни. Удачи в ваших векторных приключениях!
Применение векторов в современном мире
Векторы — это не только математическая концепция, но и мощный инструмент, используемый в различных областях нашей современной жизни
В этом статье мы расскажем о практическом применении векторов и их важности в компьютерной графике, медицине, авиации и спорте
Примеры задачи на нахождение координат вектора
Задача 1
Существуют пары точек:
\(A(-3; 7), B(2; -1)\);
\(С(5; 0), D(11; 8).
\)
Необходимо определить координаты векторов:
\(\overrightarrow {AB} ,\overrightarrow {CD} .\)
Решение:
С целью вычисления координат вектора необходимо из координат его конца (точки B) вычесть координаты начала (точки A):
\(\overrightarrow {AB} (2 — ( — 3); — 1 — 7)\)
\(\overrightarrow {AB} (5; — 8).\)
Аналогичным способом можно рассчитать координаты второго вектора:
\(\overrightarrow {CD} (11 — 5;8 — 0)\)
\(\overrightarrow {CD} (6;8)\)
Ответ: \(\overrightarrow {AB} (5; — 8); \overrightarrow {CD} (6;8).\)
Задача 2
Требуется вычислить координаты вектора \(\overline{AB}\) при условии, что:
\(A\left(-1;\; 2\right),\ B\left(2;\; -3\right)\)
Решение
Определить координаты, которым характеризуется вектор \(\overline{AB}\), исходя из известных по заданию координат его начальной точки \(A\left(-1;\; 2\right)\) и конечной точки \(B\left(2;\; -3\right)\), можно путем вычитания из координат конечной точки соответствующих координат начальной точки. Таким образом, первым и единственным действием в данном случае является:
\(\overline{AB}=\left(2-\left(-1\right)\, ;\; -3-2\right)=\left(3;\; -5\right)\)
Ответ: \(\overline{AB}=\left(3;\; -5\right)\)
