Матричный полином

Алгоритм и методы расчета

Существует несколько методов расчета значения матричного многочлена, включая метод простой подстановки, метод степенных рядов и метод Кэли-Хамильтона.

Метод простой подстановки заключается в поэлементной замене неизвестных матрицы на числовую матрицу и последующем вычислении каждого элемента полученной матрицы. Этот метод прост в использовании, но может быть неэффективен при больших размерах матрицы.

Метод степенных рядов основан на разложении матричного многочлена в бесконечный степенной ряд, который затем можно суммировать для получения числовой матрицы. Этот метод особенно полезен при наличии дополнительной информации о матрице, такой как ее спектральное разложение.

Метод Кэли-Хамильтона позволяет найти значение матричного многочлена, используя характеристический полином матрицы. В этом методе каждый элемент подставляется в многочлен и затем вычисляется сумма по степеням матрицы. Этот метод особенно полезен при работе с квадратными матрицами.

Выбор метода расчета значения матричного многочлена зависит от его структуры и доступной информации о матрице. Все они представляют собой алгоритмы, которые можно реализовать в программном коде для автоматического вычисления значений матричных многочленов.

Определение граничных условий для матричного многочлена

Граничные условия для матричного многочлена определяются в зависимости от конкретной задачи и свойств матрицы. Они играют важную роль при решении матричных уравнений и нахождении матричных многочленов.

Одним из наиболее распространенных типов граничных условий является условие нулевой граничной точки. В этом случае требуется, чтобы матричный многочлен обращался в ноль в заданной граничной точке. Такое условие часто применяется при решении задач с волновыми функциями и доопределении операторов.

Другим типом граничных условий является условие периодическости. Здесь требуется, чтобы матричный многочлен обладал периодическими свойствами в определенных интервалах или точках. Это условие широко используется в задачах с осцилляторами, затворами и другими системами с периодическим поведением.

Кроме того, могут быть заданы и другие типы граничных условий, которые зависят от конкретной физической задачи или математической модели

Важно правильно формулировать эти условия и учитывать их при нахождении матричного многочлена

Сходимость и область сходимости матричного многочлена

Сходимость матричного многочлена обычно определяется с использованием понятия спектра матрицы. Спектр матрицы — это множество всех собственных значений матрицы. Если все собственные значения матрицы находятся внутри некоторого круга в комплексной плоскости, то матричный многочлен сходится.

Если существуют собственные значения, которые лежат на границе круга, то матричный многочлен сходится только для матриц, у которых все собственные значения внутри круга. Область сходимости в этом случае является открытым кругом в комплексной плоскости.

Область сходимости матричного многочлена может быть найдена с использованием алгоритмов численного анализа, таких как метод Гершгорина или метод Хаусхолдера. Эти методы позволяют оценить спектр матрицы и найти круг, содержащий все собственные значения.

Знание области сходимости матричного многочлена позволяет более эффективно вычислять его значение, так как можно использовать специализированные алгоритмы для матриц, которые попадают в область сходимости

Таким образом, изучение сходимости и области сходимости матричного многочлена является важной задачей в математике и численном анализе

Примеры применения матричного многочлена

Матричный многочлен используется в различных областях математики и физики, где матрицы используются для описания и анализа систем или процессов. Вот несколько примеров, где матричный многочлен находит свое применение:

1. Теория управления: В области теории управления матричные многочлены используются для моделирования и анализа динамических систем. Они позволяют описать связи между различными переменными в системе и определить ее поведение в зависимости от различных параметров. Матричные многочлены используются для проектирования и оптимизации систем управления, таких как автоматические регуляторы и фильтры.

2. Квантовая механика: В квантовой механике матрицы используются для представления операторов физических величин и их состояний. Матричные многочлены позволяют вычислять значения наблюдаемых величин в зависимости от состояний системы и времени. Они также используются для решения уравнений Шредингера и анализа эволюции квантовых систем.

3. Теория графов и транспорта: В теории графов и транспорта матричные многочлены используются для описания и анализа сетевых структур и их свойств. Они позволяют вычислить различные характеристики графа, такие как кратчайшие пути или потоки, а также определить его связность и устойчивость. Матричные многочлены также используются для моделирования транспортной системы и оптимизации расписания и маршрутов.

Это лишь несколько примеров, в которых матричные многочлены находят применение. Они также используются в других областях математики, физики и инженерии для решения различных задач и моделирования сложных систем.

Объединение массивов

Массивы можно Объединенять. Есть горизонтальное и вертикальное
объединение.

a = np.floor(10*np.random.random((2,2)))
b = np.floor(10*np.random.random((2,2)))

print(a)
print(b)
print()


print(np.vstack((a,b)))
print()

print(np.hstack((a,b)))

 ]

 ]


 
 
 ]


 ]

Массивы можно переформировать при помощи метода, который задает новый
многомерный массив. Следуя следующему примеру, мы переформатируем
одномерный массив из десяти элементов во двумерный массив, состоящий из
пяти строк и двух столбцов:

a = np.array(range(10), float)
print(a)
print()

# Превратим в матрицу
a = a.reshape((5, 2))
print(a)
print()

# Вернем обратно
print(a.flatten())

# Другой вариант
print(a.reshape((-1)))
# Превратим в марицу (9, 1)
print(a.reshape((-1, 1)))
# Превратим в марицу (1, 9)
print(a.reshape((1, -1)))

 
 
 
 ]




 
 
 
 
 
 
 
 
 ]
`0`.` 1`.` 2`.` 3`.` 4`.` 5`.` 6`.` 7`.` 8`.` 9`.``

мономиальный

Алгебраическое выражение, содержащее только один ненулевой член, называется мономом. Одночлен — это тип многочлена, например, биномиального и трехчленного, который представляет собой алгебраическое выражение, имеющее только один член, не равный нулю. Он состоит только из одного термина, что позволяет легко выполнять операции сложения, вычитания и умножения.

Примеры:

Различные части мономиального выражения:

• Переменная: буквы, присутствующие в выражении монома, являются переменными.
• Коэффициент : число перед переменной или число, умноженное на переменную в выражении.
• Буквенная часть: алфавиты, присутствующие вместе со значениями экспоненты, являются буквальной частью.

Рассмотрим пример 6xy 2 — мономиальное выражение,

• Коэффициент равен 6
• Переменные x и y
• Степень мономиального выражения = 1 + 2 = 3
• Буквальная часть xy 2

Мономиальная степень

Сумма значений показателей степени переменных в выражении называется степенью монома или мономиальной степенью. Если переменные не имеют значений экспоненты, их неявное значение равно 1.

Пример:

Мономиальные операции

Арифметические операции, которые выполняются над мономом, это сложение, вычитание, умножение и деление.

Сложение двух мономов:

Когда мы добавляем два одночлена с одной и той же литеральной частью, это приводит к одночленному выражению.

Пример:

Вычитание двух мономов:

Когда мы вычитаем два одночлена с одной и той же буквенной частью, это приводит к одночленному выражению.

Умножение двух мономов:

Когда мы умножаем два одночлена с одной и той же буквенной частью, это приводит к одночленному выражению.

Деление двух мономов:

Когда мы делим два одночлена с одной и той же буквенной частью, это приводит к одночленному выражению.

Что представляет собой матричный многочлен?

Матричный многочлен удобен для описания различных математических моделей и систем, которые включают матрицы. Он может быть использован для аппроксимации и анализа сложных задач, таких как системы дифференциальных уравнений, теория управления и множество других областей математики и физики.

Значение матричного многочлена – это результат применения данной функции к конкретной матрице. Иными словами, это матрица, полученная путем подстановки значений матричных переменных и констант в алгебраическое выражение матричного многочлена.

Чтобы найти значение матричного многочлена, нужно подставить значения матричных переменных и констант в выражение многочлена и выполнить необходимые математические операции. Полученная матрица будет являться значением матричного многочлена для заданных значений переменных.

Полиномиальный

Алгебраическое выражение, содержащее один, два или более члена, называется полиномом.

Примеры:

Типы многочленов

• Моном: алгебраическое выражение, содержащее только один ненулевой член, называется мономом. Одночлен — это тип многочлена, например, биномиального и трехчленного, который представляет собой алгебраическое выражение, имеющее только один член, не равный нулю.
• Бином: алгебраическое выражение, содержащее два ненулевых члена, называется биномом. Оно выражается в виде ax m + bx n , где a и b — числовые значения, x — переменная, m и n — различные неотрицательные целые числа.
• Трехчлен: алгебраическое выражение, содержащее три ненулевых члена, называется трехчленом. Например, a + b + c — трехчлен от трех переменных a, b и c.

Степень многочлена

В полиномиальном уравнении переменная, имеющая наибольший показатель степени, называется степенью полинома.

Пример:

Полиномиальные уравнения

Стандартная форма представления полиномиального уравнения состоит в том, чтобы сначала поставить высшую степень, а в последнюю очередь постоянный член.

Пример:

Решение полиномов

Мы можем легко решать многочлены, используя основные понятия алгебры и факторизации, в то время как первый шаг решения многочленов — установить правую часть на 0.

Решение линейного многочлена:

1. Первым шагом является выделение переменного члена
2. Далее приравняем уравнение к 0
3. Решите его, используя основные операции алгебры.

Пример: решить 4a – 8?

Решение:

Решение квадратного полинома:

1. Первый шаг — переписать выражение в порядке убывания степени.
2. Далее приравнять к 0
3. Выполните полиномиальную факторизацию.

Пример: решить 4a 2 – 4a + a 3 – 16?

Решение:

Как найти значение f(a) методом подстановки?

Метод подстановки — это один из основных методов вычисления значения матричного многочлена f(a). Данный метод основывается на подстановке матрицы a вместо переменной x в выражение, задающее многочлен f(x), и последующей простой арифметической операции.

Для нахождения значения f(a) методом подстановки необходимо:

• Задать выражение, задающее матричный многочлен f(x)
• Подставить матрицу a вместо переменной x в данное выражение
• Выполнить необходимые арифметические операции

Например, пусть задано выражение f(x) = x^2 — 3x + 2. Необходимо найти значение f(a), где a = , ].

Подставляем a вместо x в выражение:

f(a) = a^2 — 3a + 2

Выполняем операции:

a^2	= , ] * , ]	= , ]
3a	= 3 * , ]	= , ]
f(a)	= , ] — , ] + 2I	= , ]

Таким образом, значение f(a) методом подстановки равно , ].

Подходить на собственном примере

Рассмотрим вещественное векторное пространство размерности 3 с базой B = ( e ₁ , e ₂ , e ₃ ). Рассмотрим затем эндоморфизм u, определяемый его следующим матричным представлением в базе B  :

ты(39-9233-3){\ displaystyle u: \; {\ begin {pmatrix} 3 & 9 & -9 \\ 2 & 0 & 0 \\ 3 & 3 & -3 \ end {pmatrix}}}

Вычисляя матричное представление u 2, а затем u 3 , находим:

ты2(618-18618-18)етты3().{\ displaystyle u ^ {2}: \; {\ begin {pmatrix} 0 & 0 & 0 \\ 6 & 18 & -18 \\ 6 & 18 & -18 \ end {pmatrix}} \ quad и \ quad u ^ {3}: \; {\ begin {pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \ end {pmatrix}}.}

Поскольку u 3 — нулевой эндоморфизм, u действительно нильпотентен с индексом 3.

Нильпотентность и многочлены

Затем определим характеристический многочлен P эндоморфизма u  :

п(Икс)знак равноDet(ты-Икся)знак равно|3-Икс9-92-Икс33-3-Икс|знак равно-Икс(3-Икс)(-3-Икс)-2(9(-3-Икс)+27)-27Иксзнак равно-Икс3.{\ Displaystyle P (X) = \ det (u-XI) = \; {\ begin {vmatrix} 3-X & 9 & -9 \\ 2 & -X & 0 \\ 3 & 3 & -3-X \ end {vmatrix}} = — X (3-X) (- 3-X) -2 (9 (-3-X) +27) -27X = -X ^ {3}.}

Имеет место равенство P ( X ) = — X 3 . В случае, когда размерность векторного пространства равна n , необходимым и достаточным условием для того, чтобы эндоморфизм был нильпотентным, является то, что его характеристический многочлен равен (- X ) n .

Теория минимальных многочленов говорит нам, что вычисление характеристического многочлена в этом примере не требуется. Многочлен X 3 отменяет эндоморфизм. Тогда минимальный многочлен является делителем этого многочлена. Однако единственный нормированный делитель (то есть чей моном высшей степени равен 1) числа — X 3, который сокращает u, является самим собой. Теорема Кэли-Гамильтона говорит нам, что минимальный многочлен делит характеристический многочлен. Тогда достаточно заметить, что характеристический многочлен имеет степень, равную размерности пространства, чтобы получить его без вычислений. Необходимым и достаточным условием нильпотентности эндоморфизма является то, что его минимальный многочлен имеет вид X p .

Нильпотентность и уменьшенная база

Рассмотрим тогда вектор e ₁ . равен 3 , и семейство ( е ₁ , у ( е ₁ ), у 2 ( е ₁ )) является свободным . Причем его кардинал — размерность пространства. Таким образом, эта семья является базой. В этой базе данных матричное представление u принимает следующий вид:

ты(11).{\ displaystyle u: \; {\ begin {pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \ end {pmatrix}}.}

Опять же, эти свойства являются общими для нильпотентного эндоморфизма. В общем случае размерности n , если x является вектором индекса p, то p меньше или равно n и семейство ( x , u ( x ),…, u p-1 ( x )) является свободным. Кроме того, всегда существует базис ( e ₁ , e ₂ ,…, e _n ) такой, что u ( e _i ) равно либо 0, либо e _{i +1} , причем u ( e _n ) = 0. C ‘равно редуцированный базис нильпотентного эндоморфизма.

Умножение матриц

Пример 7
. Даны матрицы и . Найти матрицы C = A·B и D = B·A.
Решение.

Прежде всего заметим, что произведение A·B существует, так как число столбцов A равно числу строк B.

Пример 8
. Дана матрица . Найти 3A 2 – 2A.
Решение.

.
; .
.
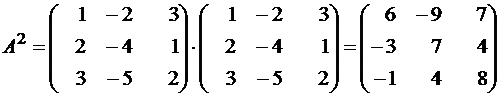Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.

С каждой
квадратной матрицей связаны два многочлена: характеристический и минимальный.
Эти многочлены играют большую роль в различных вопросах теории матриц. Так,
например, понятие о функции от матрицы, которое мы введем в следующей главе,
будет целиком основываться на понятии о минимальном многочлене матрицы. В этой
главе рассматриваются свойства характеристического и минимального многочлена.
Этому исследованию предпосылаются основные сведения о многочленах с матричными
коэффициентами и о действиях над ними.

§ 1. Сложение и умножение матричных многочленов

Рассмотрим
квадратную многочленную матрицу , т. е. квадратную матрицу, элементами
которой являются многочлены относительно (с коэффициентами из данного
числового поля ):

Матрицу можно представить
в виде многочлена с матричными коэффициентами, расположенного по степеням :

. (3)

Число называется степенью
многочлена, если .
Число называется
порядком многочлена. Многочлен (1) будем называть регулярным,
если .

Многочлен с
матричными коэффициентами мы будем иногда называть матричным многочленом.
В отличие от матричного многочлена обычный многочлен со скалярными
коэффициентами будем называть скалярным многочленом.

Рассмотрим
основные действия над матричными многочленами. Пусть даны два матричных
многочлена одного и того же порядка и . Обозначим через наибольшую из степеней этих
многочленов. Эти многочлены можно записать в виде

т. е. сумма
(разность) двух матричных многочленов одного и того же порядка может быть
представлена в виде многочлена, степень которого не превосходит наибольшей из
степеней данных многочленов.

Пусть даны два
матричных многочлена и степеней и одного и того же порядка :

Если бы мы
перемножили на
(т. е. изменили
бы порядок сомножителей), то мы получили бы, вообще говоря, другой многочлен.

Умножение
матричных многочленов обладает еще одним специфичным свойством. В отличие от
произведения скалярных многочленов произведение матричных многочленов (4) может
иметь степень, меньшую , т. е. меньшую суммы степеней
сомножителей. Действительно, в (4) произведение матриц может равняться нулю при и . Однако, если хотя
бы одна из матриц и неособенная, то из и следует: . Таким образом, произведение
двух матричных многочленов равно многочлену, степень которого меньше или равна
сумме степеней сомножителей. Если хотябы один из двух сомножителей регулярный
многочлен, то в этом случае степень произведения всегда равна сумме степеней
сомножителей.

Матричный
многочлен -го
порядка можно
записать двояко:

Обе записи при
скалярном дают
один и тот же результат. Однако если мы пожелаем вместо скалярного аргумента подставить
квадратную матрицу -го порядка , то результаты подстановок
в (5) и (5″) будут, вообще говоря, различны, так как степени матрицы могут не быть
перестановочными с матричными коэффициентами .

и будем называть
правым,
а левым
значением матричного многочлена при подстановке вместо матрицы .

Рассмотрим снова
два матричных многочлена

,

и их произведение

Преобразования в
тождестве (7″) сохраняют свою силу при замене матрицей -го порядка , если только
матрица перестановочна
со всеми матричными коэффициентами . Аналогично в тождестве (7″)
можно заменить скаляр матрицей , если матрица перестановочна со
всеми коэффициентами . В первом случае получаем: любой матрицей -го порядка всегда справедливы
тождества

, . (9)

Как найти матричный многочлен

Матричный многочлен выражается из полинома, в котором множители являются квадратными матрицами. Чтобы найти матричный многочлен, необходимо умножить саму матрицу на себя m раз, где m — порядок матрицы.

Для определения матричного многочлена степени n необходимо выполнить следующие действия:

1. Найти собственные значения матрицы
2. По собственным значениям найти собственные векторы матрицы
3. Составить фундаментальную матрицу
4. Выразить искомый матричный многочлен через фундаментальную матрицу

Для упрощения вычислений матричный многочлен можно представить в виде суммы некоторых многочленов, каждый из которых имеет вид cA^k, где A — исходная матрица, а c — константа. Коэффициенты c можно найти, подставив в выражение для матричного многочлена значения k от 0 до n — 1.

Также существует специальный метод для нахождения матричного многочлена, аналогичный нахождению обычного числового многочлена методом Горнера. Он заключается в последовательном вычислении текущего значения многочлена через умножение матрицы на каждой итерации.

Пример вычисления матричного многочлена
n
Матрица
Многочлен

1

1

I

1

2	1
-1

A

2

3	2
-2	-1

A^2

3

4	3
-3	-2

A^3

В чем состоит значение матричного многочлена?

Значение матричного многочлена можно найти, используя процесс подстановки матрицы вместо переменных в каждом члене многочлена и последующего вычисления всех операций между матрицами. Для этого нужно уметь умножать матрицы, складывать их и производить другие матричные операции.

Чтобы вычислить значение матричного многочлена, следует следовать определенному порядку операций: сначала требуется вычислить каждый член многочлена, подставив в него матрицу вместо переменных. Затем нужно сложить все полученные члены многочлена и упростить получившееся выражение.

Значение матричного многочлена имеет важное значение в различных областях науки и техники, таких как физика, экономика, компьютерные науки и др. Оно позволяет моделировать и анализировать сложные системы, в которых вместо обычных чисел используются матрицы, что упрощает решение сложных задач и позволяет получить более точные результаты

Пример	Значение матричного многочлена

Применение и преимущества

1. Криптография: Матричные многочлены применяются для шифрования и дешифрования данных. Использование матричных многочленов в криптографии обеспечивает высокую степень защиты информации.
2. Теория управления: Матричные многочлены используются для моделирования и анализа динамических систем. Они позволяют описывать поведение системы во времени и прогнозировать ее будущее состояние.
3. Теория вероятностей: Матричные многочлены находят применение при решении задач, связанных с распределениями и стохастическими процессами. Они позволяют анализировать случайные процессы и вычислять вероятности различных событий.
4. Машинное обучение: Матричные многочлены используются для обработки и анализа больших объемов данных. Они позволяют эффективно работать с матричными структурами данных, такими как изображения, тексты, звуки и другие.

Преимущества использования матричного многочлена включают:

• Универсальность: Матричные многочлены могут быть применены для моделирования различных систем и процессов, что делает их универсальным инструментом в научных и технических исследованиях.
• Высокая точность: Использование матричных многочленов позволяет проводить точные вычисления и получать достоверные результаты.
• Высокая скорость вычислений: Матричные многочлены могут быть эффективно вычислены с использованием специальных методов и алгоритмов, что позволяет сократить время выполнения операций.
• Удобство использования: Матричные многочлены обладают простой и интуитивно понятной структурой, что упрощает их использование и анализ.

В целом, значение матричного многочлена и его применение имеют большое значение для решения широкого спектра задач в различных научных и технических областях.

Примеры нахождения значения матричного многочлена

Рассмотрим несколько примеров, чтобы лучше понять процесс нахождения значения матричного многочлена.

Пример 1:

Дан матричный многочлен p(A) = A^2 — 3A + 2I, где A — некоторая квадратная матрица, I — единичная матрица. Найдём значение многочлена для матрицы A = .

Подставим матрицу A вместо A в многочлен и выполним операции:

p(A) = (A^2 — 3A + 2I) = (^2 — 3 + 2)

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ = — 3 + 2

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ = — +

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ =

Таким образом, значение матричного многочлена p(A) для матрицы A = равно .

Пример 2:

Рассмотрим матричный многочлен p(A) = 2A^3 — A^2 + 5A — 4I и матрицу A = .

Подставим значение матрицы в многочлен и произведём необходимые операции:

p(A) = 2()^3 — ()^2 + 5() — 4

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ = 2( * * ) — ( * ) + 5 —

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ = 2( * ) — ( * ) + —

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ = 2( * ) — ( * ) + —

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ = — + —

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ =

Таким образом, значение матричного многочлена p(A) для матрицы A = равно .

Биномиальный

Алгебраическое выражение, содержащее два ненулевых члена, называется биномом. Оно выражается в виде ax m + bx n , где a и b — числовые значения, x — переменная, m и n — различные неотрицательные целые числа.

Примеры:

Любое уравнение, содержащее один или несколько биномов, называется биномиальным уравнением.

Пример:

Операции над биномами

Несколько основных операций над биномами

• Факторизация
• Добавление
• вычитание
• Умножение
• Возведение в энную степень
• Преобразование в биномы более низкого порядка

Факторизация:

Бином можно представить как произведение двух других.

Пример:

Добавление:

Можно добавить два бинома, если оба содержат одну и ту же переменную и один и тот же показатель степени.

Пример:

Вычитание:

Это похоже на сложение, два бинома должны содержать одну и ту же переменную и показатель степени.

Пример:

Умножение:

Когда мы умножаем два бинома, используется распределительное свойство, и в итоге получается четыре члена. В этом методе умножение осуществляется путем умножения каждого члена первого множителя на второй множитель.

Пример:

Возведение в энную степень:

Бином можно возвести в n-ю степень и выразить в виде (x + y) n

Преобразование в биномы более низкого порядка:

Биномы более высокого порядка могут быть разложены на биномы более низкого порядка, такие как кубы, могут быть разложены на произведения квадратов и другого одночлена.

Пример: