Как определить, что числа попарно различны?
Чтобы определить, что числа попарно различны, нужно проверить, что все числа в наборе не повторяются и не совпадают друг с другом.
Для этого необходимо выполнить следующие действия:
- Составить набор чисел: выберите любое количество чисел, которые хотите проверить на попарную различность.
- Проверить наличие повторений: просмотрите весь набор и убедитесь, что каждое число встречается только один раз. Если в наборе есть повторяющиеся числа, то они не являются попарно различными.
- Сравнить все числа друг с другом: сравните каждое число в наборе со всеми остальными числами. Если хотя бы одно число совпадает с другим числом, то набор не является попарно различным.
Попарно различные числа означают, что каждое число в наборе отличается от всех остальных чисел и не повторяется. Наличие повторений или совпадений в наборе делает его неподходящим для условия попарной различности.
Проверяя числа на попарную различность, можно убедиться, что все числа в наборе действительно уникальны и не совпадают друг с другом. Это может быть полезным при решении определенных математических или программных задач, где требуется работать с наборами попарно различных чисел.
Критерии попарной различности
Для определения попарной различности чисел необходимо выполнение нескольких критериев:
- Каждое число должно быть уникальным и не повторяться среди остальных чисел.
- Попарно различные числа не могут иметь никаких общих элементов или свойств. Если два числа имеют хотя бы одно общее свойство, они не являются попарно различными.
- Попарно различные числа должны быть различными на всех уровнях сравнения. Например, если есть два числа, то необходимо проверить их различие как в целом, так и в отдельных разрядах или десятичных позициях.
Таким образом, попарно различные числа могут быть определены только при выполнении указанных критериев. Их соблюдение позволяет гарантировать факт полного отсутствия любого сходства или повторения между числами.
Применение алгоритмов для определения попарной различности чисел
Для определения попарной различности чисел можно применять различные алгоритмы. Один из простых способов — это использование двойного цикла. Перебираются все пары чисел из заданного множества, и проверяется, что оба числа различны:
В этом алгоритме каждая пара чисел проверяется только один раз, поэтому он имеет временную сложность O(n^2), где n — количество чисел в множестве. Если количество чисел велико, то этот алгоритм может быть неэффективным.
Еще одним эффективным алгоритмом может являться использование структуры данных Set. Set — это коллекция уникальных значений, и добавление элемента в Set не происходит, если такое значение уже существует. Для определения попарной различности чисел можно добавить все числа из заданного множества в Set и затем проверить, что размер Set равен размеру множества чисел:
В этом алгоритме используется один проход по всем числам, и добавление числа в Set происходит за константное время O(1). Таким образом, алгоритм имеет временную сложность O(n), где n — количество чисел в множестве.
Выбор алгоритма для определения попарной различности чисел зависит от конкретной задачи и требований к производительности. При работе с небольшими множествами чисел можно использовать более простые алгоритмы, а при работе с большими множествами лучше выбрать более эффективные алгоритмы.
Попарно простые числа – определения и примеры
Через взаимно простые числа дается определение попарно простых чисел.
Определение.
Целые числа a1, a2, …, ak, каждое из которых взаимно просто со всеми остальными, называют попарно простыми числами.
Приведем пример попарно простых чисел. Числа 14, 9, 17, и −25 – попарно простые, так как пары чисел 14 и 9, 14 и 17, 14 и −25, 9 и 17, 9 и −25, 17 и −25 представляют собой взаимно простые числа. Здесь же заметим, что попарно простые числа всегда являются взаимно простыми.
С другой стороны, взаимно простые числа далеко не всегда являются попарно простыми, это подтверждает следующий пример. Числа 8, 16, 5 и 15 не являются попарно простыми, так как числа 8 и 16 не взаимно простые. Однако, числа 8, 16, 5 и 15 – взаимно простые. Таким образом, 8, 16, 5 и 15 – взаимно простые числа, но не попарно простые.
Следует особо выделить совокупность некоторого количества простых чисел. Эти числа всегда являются и взаимно простыми и попарно простыми. Например, 71, 443, 857, 991 – и попарно простые, и взаимно простые числа.
Также понятно, что когда речь идет о двух целых числах, то для них понятия «попарно простые» и «взаимно простые» совпадают.
Список литературы.
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
- Виноградов И.М. Основы теории чисел.
- Михелович Ш.Х. Теория чисел.
- Куликов Л.Я. и др. Сборник задач по алгебре и теории чисел: Учебное пособие для студентов физ.-мат. специальностей педагогических институтов.
Как появились числа Фибоначчи
Первым эту последовательность описал итальянский учёный Леонардо Пизанский по прозвищу Фибоначчи. Он жил в XII веке и усердно изучал работы античных и индийских математиков. В них Леонардо нашёл много полезных знаний — например, что десятичная система удобнее, чем римская нотация, и что по ней проще считать.

Портрет Леонардо ПизанскогоИзображение: I benefattori dell’umanita. L. Ducci e C., 1850 / National Library of Naples / Icas94 / DeAgostini / Getty Images
Полученные знания Леонардо систематизировал в своём главном труде — «Книге абака». Там же появилось и первое упоминание о числах Фибоначчи — как ни странно, в контексте решения задачи о кроликах:
Задача о размножении кроликов
В огороженный загон посадили двух кроликов — самку и самца. Каждый месяц пара являет миру ещё одну пару кроликов. Вопрос: сколько пар кроликов будет в загоне через год?
Конечно, решить эту задачу не так просто, потому что на размножение кроликов влияет много факторов — например, они могут умереть или убежать. Поэтому Леонардо ограничил задачу такими условиями:
- кролики не могут умереть;
- они достигают половой зрелости за месяц;
- самки беременны ровно месяц;
- кролики всегда рождаются парами: самка + самец.
Теперь задачу вполне можно решить: ответом на неё как раз будет последовательность Фибоначчи. Логика такая: каждая взрослая пара кроликов будет создавать ещё одну пару через месяц после рождения. Эти кролики-дети будут расти месяц, а потом размножаться с другими кроликами. И так двенадцать месяцев.
Чуть лучше этот процесс можно представить с помощью этой схемы:

Инфографика: Magicleaf / Shutterstock / Майя Мальгина для Skillbox Media
Смотрите, первая пара кроликов ещё совсем молодая, поэтому пока не может дать потомство. Но уже через месяц кролики подрастут и смогут размножаться — соответственно, на третий месяц пар будет уже две. Дальше количество пар будет равняться сумме пар за два предыдущих месяца, и последовательность примет уже знакомый нам вид:

Изображение: Skillbox Media
Получаем ответ на задачу: 233 пары кроликов.
Наибольшее отрицательное и наименьшее положительное целое число
Со сравнением двух целых чисел мы полностью разобрались в предыдущих разделах этой статьи. Сейчас мы еще вкратце остановимся на сравнении трех и большего количества целых чисел, и разберем возникающие при этом ситуации.
Когда сравниваются три и более числа, то сначала проводится сравнение всех возможных пар, составленных из этих чисел. Например, при сравнении четырех целых чисел 7, 17, и −2 попарно сравниваются 7 и 17, 7 и , 7 и −2, 17 и , 17 и −2, и −2, при этом получаются следующие результаты 7<17, 7>0, 7>−2, 17>0, 17>−2 и 0>−2. После этого полученные результаты объединяются в цепочку неравенств (и равенств, когда есть равные числа). Для этого исходные числа записываются в порядке возрастания от самого меньшего до самого большего и между двумя соседними числами ставятся знак < (и знак = между равными числами). В нашем примере цепочка неравенств будет иметь следующий вид −2<0<7<17.
При сравнении нескольких чисел возникает понятие наибольшего и наименьшего числа.
Определение.
Число, которое меньше любого другого числа из рассматриваемого множества чисел, называется наименьшим числом в данном множестве.
Определение.
Число, которое больше любого другого числа в рассматриваемом множестве чисел, называется наибольшим числом в данном множестве.
Проще говоря, наибольшее число – это самое большое число в данном множестве чисел, а наименьшее число – это самое маленькое число.
Приведем пример наибольшего и наименьшего целого числа в множестве, состоящем из шести целых чисел −4, −81, −4, 17, и 17. Результат сравнения этих чисел имеет вид −81<−4=−4<0<17=17. Отсюда хорошо видно, что число −81 является наименьшим целым числом в рассматриваемом множестве, а число 17 – наибольшим целым числом в этом множестве.
Вообще все числа из множества целых чисел можно записать в порядке возрастания (каждое следующее число больше предыдущего), при этом получим последовательность целых чисел вида …, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, … Эту последовательность целых чисел можно также записать в виде бесконечной цепочки неравенств: …<−5<−4<−3<−2<−1<0<1<2<3<4<5<…
Отсюда видно, что в множестве целых чисел не существует ни наибольшего целого числа, ни наименьшего целого числа. Действительно, всегда можно указать целое число, которое больше любого наперед заданного сколь угодно большого целого числа (им будет любое следующее число в последовательности целых чисел). Аналогично можно указать целое число, которое меньше любого наперед заданного сколь угодно малого целого числа (это любое число, предшествующее заданному числу в последовательности целых чисел).
Однако во множестве целых положительных чисел (1, 2, 3, …) существует наименьшее целое число – это число 1. Во множестве целых неотрицательных чисел (0, 1, 2, 3, …) наименьшим числом является число . Целое положительное число в только что указанных множествах мы указать не можем.
Число нуль является наибольшим целым неположительным числом (во множестве целых неположительных чисел …, −3, −2, −1, 0). А −1 (минус один) – это наибольшее целое число в множестве целых отрицательных чисел (…, −3, −2, −1). Наименьшего целого числа эти множества не имеют.
Список литературы.
Рациональные числа и их отношение к другим классам чисел
Рациональные числа включают в себя как целые числа, так и натуральные числа. Натуральные числа — это числа, которые используются для подсчета предметов или организации событий, например, 1, 2, 3 и т.д. Целые числа — это натуральные числа вместе с отрицательными числами, например, -1, -2, -3 и т.д.
Рациональные числа также относятся к классу действительных чисел, которые включают в себя как рациональные числа, так и иррациональные числа. Иррациональные числа — это числа, которые не могут быть представлены в виде дроби и обладают бесконечным непериодическим десятичным представлением. Примерами иррациональных чисел являются корень из 2, число Пи и т.д.
Сравнение и взаимоотношение классов чисел:
1. Натуральные числа можно рассматривать как основу для построения целых и рациональных чисел. Целые числа включают в себя натуральные числа, а также добавляют отрицательные числа. Рациональные числа включают в себя как натуральные, так и целые числа, а также добавляют числа, представимые в виде дробей.
2. Действительные числа включают в себя как рациональные, так и иррациональные числа. Рациональные числа могут быть представлены в виде десятичных дробей, как периодических, так и непериодических. Иррациональные числа не могут быть представлены в виде десятичных дробей и имеют бесконечное непериодическое десятичное представление.
3. Все классы чисел — натуральные, целые, рациональные, иррациональные и действительные — вместе образуют множество всех чисел. Это множество называется числовой прямой.
Особенности попарно различных чисел
Особенностью попарно различных чисел является отсутствие повторяющихся значений в данном наборе чисел. Каждое число в этом наборе является уникальным и не имеет дубликатов.
Например, набор чисел {1, 2, 3, 4, 5} является попарно различным, так как каждое число отличается от других чисел в этом наборе. Если бы в этом наборе было повторяющееся число, например, {1, 2, 2, 4, 5}, то данный набор уже не был бы попарно различным.
Особенность попарно различных чисел важна во многих областях, включая математику, программирование и статистику. В некоторых задачах требуется обработка и анализ данных, где необходимо рассматривать только уникальные числа. Понимание особенностей попарно различных чисел помогает в решении таких задач.
Гибкое использование
Гибкое использование попарно различных чисел можно продемонстрировать на примере таблицы. Ниже приведена таблица, в которой каждое число представлено в ячейке таблицы:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Здесь видно, что каждое число в таблице уникально и различно от остальных чисел. Такая уникальность и различие между числами позволяют проводить различные операции над ними, такие как сложение, вычитание, умножение и деление.
Гибкое использование попарно различных чисел также позволяет применять их в различных областях науки, например, в физике, экономике, компьютерной науке и других дисциплинах. Благодаря своей универсальности и точности, попарно различные числа становятся незаменимым инструментом для решения сложных задач и достижения точных результатов.
В алгебре попарно различные числа используются, например, при работе с множествами и функциями. Они позволяют строить корректные и последовательные доказательства и утверждения. Кроме того, использование попарно различных чисел в алгебре помогает избежать ошибок и парадоксов, которые могут возникнуть при работе с равными числами.
В теории вероятности попарно различные числа обеспечивают правильное определение вероятностей событий. Они гарантируют, что два разных события не будут считаться одним и тем же, что является основой для корректного расчета вероятностей и проведения испытаний.
В статистике попарно различные числа помогают устранить проблемы связанные с повторением данных и искажением результатов исследований. Они позволяют проводить независимые и сравнимые исследования, что является ключевым требованием в этой области науки.
Таким образом, использование попарно различных чисел в алгебре, теории вероятности и статистике имеет большое значение, поскольку оно обеспечивает правильность и достоверность результатов исследований и вычислений.
Уникальность и разнообразие
Примеры попарно различных чисел:
- 37 и 42 — эти числа не имеют общих цифр и различаются в каждой цифре.
- 159 и 267 — в этих числах нет общих цифр, они уникальны и различаются в каждой позиции.
- 804 и 623 — эти числа не имеют общих цифр, они разнообразны и представляют разные комбинации цифр.
Особенность попарно различных чисел заключается в их уникальности, что позволяет использовать их в разных областях. Например, для создания уникальных паролей, составления различных комбинаций чисел, решения логических задач и др. Они помогают представить различные варианты и решения, что способствует расширению кругозора и развитию логического мышления.
Видео:Сложение и вычитание рациональных чисел. 6 класс.Скачать
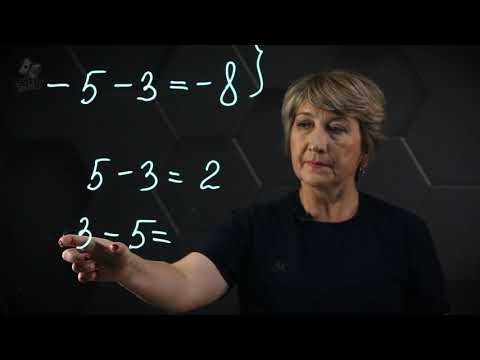
Определение понятия
Когда говорят о терминах, попарно различными они называются только в том случае, если они не идентичны друг другу и не могут быть заменены друг на друга. Если два объекта очень похожи друг на друга, но имеют малейшие отличия, то их можно считать попарно различными.
Например, банан и авокадо — это два попарно различных фрукта. Они очень похожи на внешний вид и размер, но имеют разные текстуры и вкусы.
Еще один пример — белая и черная кошка. Они обе являются кошками, но их окрас отличается. Поэтому они могут быть описаны как попарно различные.
Также в математике попарное различие может быть определено как свойство, при котором каждый элемент множества отличается от других элементов этого же множества.
Таким образом, попарное различие — это важное свойство объектов, которое позволяет проводить различные сравнения и анализы в разных областях знаний
Отличие попарной различности от обычной различности
Обычная различность, наоборот, предполагает отсутствие равенства двух или более чисел в наборе. В этом случае для обычной различности не требуется, чтобы каждое число отличалось от всех остальных чисел.
Примеры попарно различных чисел:
Набор чисел {1, 2, 3} обладает попарной различностью, так как 1 ≠ 2, 1 ≠ 3 и 2 ≠ 3.
Набор чисел {1, 1, 2} не обладает попарной различностью, так как 1 = 1, хотя число 2 отличается от 1 и 1.
Примеры наборов чисел с обычной различностью:
Набор чисел {1, 2, 3} обладает обычной различностью, так как все числа в наборе различные.
Набор чисел {1, 1, 2} не обладает обычной различностью, так как два числа 1 равны между собой.
Свойства взаимно простых чисел и их доказательства
У таких чисел есть ряд свойств и особенностей. Давайте посмотрим на них, разберем на практике и докажем их правдивость.
Свойства
Свойство — 1
Если разделить числа a и b на их общий делитель, то полученные числа будут взаимно простыми.
a : НОД (a, b) и b: НОД (a, b) будут взаимно простыми.
Свойство — 2
Условие взаимной простоты чисел – существование целых чисел \ и \ при значениях которых, следующее равенство будет верно:
\. Эта формула называется – соотношение Безу.
Доказательство свойства 2:
Пусть данное равенство будет верно a · u+ b · v= 1. Так как, НОД чисел (a, b) делит и одно и второе, то исходя из свойств делимости НОД может делить сумму чисел a · u+ b · v. Значит он может делить их и на 1. Такое условие будет возможно только в том случае, если НОД (a, b) будет равен 1. Из этого следует, что НОД = 1. Что и требовалось доказать.
Свойства
Свойство 3
Если число a и число b будут взаимно простыми, а их произведение обозначим, как c. В
такой ситуации, a · с будет делиться на b. Из этого следует, что и c будет делиться наb.
Так, как числа a, b являются взаимно простыми, то исходя из Свойства 2, можно получить
следующее равенство: \.
Если каждую часть уравнения перемножить на c, получим следующее:
\.
Слагаемое суммы \ можно разделить на число b. Так как,
число ac делится на b. Второе слагаемое тоже будет делиться на число b. Почему? Потому
что,
один из множителей будет равен числу b.
Вывод: вся сумма будет делиться на число b, так как,
\.
Следовательно, c будет делиться на b.
Свойство 4
Если числа a, b являются взаимно простыми, то и НОД (ac, b) будет равен НОД (c, b)
Наибольший общий делитель (ac, b) делит и ac и число b.
Следовательно, он будет делить и произведение чисел bc. Это значит, что НОД (ac, b) делит и ac
и bc. Исходя
их свойств НОД, он будет делить и НОД чисел (ac, bc), который по своим свойствам равен числу c.
Отсюда следует, что наибольший общий делитель чисел (ac, b) делит и b и c, а значит, что и
делит НОД (c, b).
Свойство 5
Возьмём числовую последовательность \. В ней все числа взаимно простые с каждым
из числовой последовательности \ (Числа k и m – натуральные), то
произведения \ и \ будут взаимно простыми.
Если, \ и \, то \ и \ являются взаимно простыми числами.
Понятие попарно простых чисел
В данной статье мы рассмотрим понятие попарно простых чисел в контексте теории натуральных чисел
Это понятие весьма важно и имеет много свойств, о которых мы поговорим в дальнейшем
По определению, натуральные числа будут называться попарно различными, если каждая пара этих чисел различна. То есть, если у нас есть два числа, то они должны быть различными, а если у нас есть три числа, то они должны быть попарно различными и так далее.
Здесь нам понадобится понятие простых чисел. Число называется простым, если оно имеет ровно два различных делителя: единицу и само число. Например, число 2 является простым, так как его делителями являются только 1 и 2. Но число 4 не является простым, так как у него есть ещё делители: 1, 2 и 4.
Примечательно, что простые числа ведут себя особенным образом в отношении делителей. Всякое натуральное число может быть разложено на простые множители. Пусть у нас имеется набор простых чисел:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29…
Здесь мы видим последовательность попарно простых чисел. С помощью этой последовательности мы можем разделить любое натуральное число на простые множители.
Доказательство этого свойства происходит с помощью таблицы, в которой каждое число делится наименьшим из его делителей из данной последовательности простых чисел. После такого деления мы получим произведение простых множителей, которое будет равно исходному числу.
Таким образом, понятие попарно простых чисел является важным свойством в теории натуральных чисел. Оно позволяет разбивать числа на их простые множители и проводить дальнейшие вычисления.
Почему попарная разность чисел важна?
Попарная разность чисел — это разность между каждыми двумя числами в наборе. Использование попарных разностей может быть полезным во многих аспектах, и вот почему:
- Анализ данных: Попарные разности чисел могут быть использованы для анализа данных и выявления интересных закономерностей. Например, попарные разности могут помочь обнаружить тренды или изменения в данных.
- Поиск аномалий: Сравнение попарных разностей чисел может помочь выявить аномалии или выбросы, которые могут быть важными для анализа или принятия решений. Например, если попарная разность между двумя числами значительно отличается от остальных разностей, это может указывать на необычное событие или причину.
- Прогнозирование: Попарные разности чисел могут быть использованы для прогнозирования будущих значений. Например, если попарная разность чисел показывает постепенное увеличение, это может указывать на то, что значения будут продолжать расти в будущем.
- Сравнение и ранжирование: Попарные разности чисел могут быть использованы для сравнения и ранжирования различных наборов данных. Например, сравнение попарных разностей между двумя наборами чисел может помочь определить, в каком наборе чисел различия более значительны.
- Оптимизация: Попарные разности чисел могут быть использованы для оптимизации процессов или конкретных значений. Например, если попарная разность чисел указывает на то, что одно значение является более эффективным или оптимальным, это может помочь принять соответствующие решения.
Все эти преимущества делают попарные разности чисел важными инструментами для анализа данных, прогнозирования и принятия решений. Они позволяют нам получить более глубокое понимание данных и использовать их в нашу пользу.
Сравнение произвольных целых чисел с нулем
Как мы уже сказали в предыдущем пункте, нуль равен нулю по определению равных целых чисел, то есть, 0=0. Вместе с этим справедливы равенства 0=−0 и −0=0. Действительно, −0 – это число, противоположное нулю, а число, противоположное нулю, есть нуль.
Когда мы говорили о сравнении натуральных чисел, то мы упоминали, что любое натуральное число больше нуля. Так как любое целое положительное число (при необходимости обращайтесь к материалу статьи положительные и отрицательные числа) является натуральным, то любое целое положительное число больше нуля.
Осталось определиться со сравнением отрицательных целых чисел с числом . Будем считать, что любое целое отрицательное число меньше нуля.
Обобщим информацию этого пункта в правило сравнения произвольного целого числа с нулем: любое целое отрицательное число меньше нуля, нуль равен нулю, а любое целое положительное число больше нуля. Это правило можно переформулировать так: нуль больше любого целого отрицательного числа, нуль равен нулю, и нуль меньше любого целого положительного числа.
Рассмотрим примеры. Каждое из целых чисел 4, 893, 10 000 больше, чем нуль, так как эти числа положительные. С другой стороны нуль меньше любого из указанных целых положительных чисел.
Приведем несколько примеров сравнения целых отрицательных чисел с нулем. Целое число −1 меньше, чем , так как −1 – отрицательное число. Аналогично, −50 меньше нуля. Нуль больше, чем целое отрицательное число −30 999.
Нужно еще сказать о принятых обозначениях. Для записи результатов сравнения используют знаки меньше и больше, которые имеют вид < и > соответственно. Например, запись −23<0 означает, что целое отрицательное число −23 меньше, чем . А тот факт, что целое положительное число 405 больше нуля можно записать как 405>0.
Что такое взаимно простые числа
Взаимно простыми могут быть как два целых числа, так и их большее количество. Для начала введем определение для двух чисел, для чего нам понадобится понятие их наибольшего общего делителя. Если нужно, повторите материал, посвященный ему.
Взаимно простыми будут два таких числа a и b , наибольший общий делитель которых равен 1 , т.е. НОД ( a , b ) = 1 .
Из данного определения можно сделать вывод, что единственный положительный общий делитель у двух взаимно простых чисел будет равен 1 . Всего два таких числа имеют два общих делителя – единицу и минус единицу.
Какие можно привести примеры взаимно простых чисел? Например, такой парой будут 5 и 11 . Они имеют только один общий положительный делитель, равный 1 , что является подтверждением их взаимной простоты.
Если мы возьмем два простых числа, то по отношению друг к другу они будут взаимно простыми во всех случаях, однако такие взаимные отношения образуются также и между составными числами. Возможны случаи, когда одно число в паре взаимно простых является составным, а второе простым, или же составными являются они оба.
Это утверждение иллюстрирует следующий пример: составные числа — 9 и 8 образуют взаимно простую пару. Докажем это, вычислив их наибольший общий делитель. Для этого запишем все их делители (рекомендуем перечитать статью о нахождении делителей числа). У 8 это будут числа ± 1 , ± 2 , ± 4 , ± 8 , а у 9 – ± 1 , ± 3 , ± 9 . Выбираем из всех делителей тот, что будет общим и наибольшим – это единица. Следовательно, если НОД ( 8 , − 9 ) = 1 , то 8 и — 9 будут взаимно простыми по отношению друг к другу.
Взаимно простыми числами не являются 500 и 45 , поскольку у них есть еще один общий делитель – 5 (см. статью о признаках делимости на 5 ). Пять больше единицы и является положительным числом. Другой подобной парой могут быть — 201 и 3 , поскольку их оба можно разделить на 3 , на что указывает соответствующий признак делимости.
На практике довольно часто приходится определять взаимную простоту двух целых чисел. Выяснение этого можно свести к поиску наибольшего общего делителя и сравнению его с единицей. Также удобно пользоваться таблицей простых чисел, чтобы не производить лишних вычислений: если одно из заданных чисел есть в этой таблице, значит, оно делится только на единицу и само на себя. Разберем решение подобной задачи.
Условие: выясните, являются ли взаимно простыми числа 275 и 84 .
Решение
Оба числа явно имеют больше одного делителя, поэтому сразу назвать их взаимно простыми мы не можем.
Вычисляем наибольший общий делитель, используя алгоритм Евклида: 275 = 84 · 3 + 23 , 84 = 23 · 3 + 15 , 23 = 15 · 1 + 8 , 15 = 8 · 1 + 7 , 8 = 7 · 1 + 1 , 7 = 7 · 1 .
Ответ: поскольку НОД ( 84 , 275 ) = 1 , то данные числа будут взаимно простыми.
Как мы уже говорили раньше, определение таких чисел можно распространить и на случаи, когда у нас есть не два числа, а больше.
Взаимно простыми целые числа a 1 , a 2 , … , a k , k > 2 будут тогда, когда они имеют наибольший общий делитель, равный 1 .
Иными словами, если у нас есть набор некоторых чисел с наибольшим положительным делителем, большим 1 , то все эти числа не являются по отношению друг к другу взаимно обратными.
Возьмем несколько примеров. Так, целые числа − 99 , 17 и − 27 – взаимно простые. Любое количество простых чисел будет взаимно простым по отношению ко всем членам совокупности, как, например, в последовательности 2 , 3 , 11 , 19 , 151 , 293 и 667 . А вот числа 12 , − 9 , 900 и − 72 взаимно простыми не будут, потому что кроме единицы у них будет еще один положительный делитель, равный 3 . То же самое относится к числам 17 , 85 и 187 : кроме единицы, их все можно разделить на 17 .
Обычно взаимная простота чисел не является очевидной с первого взгляда, этот факт нуждается в доказательстве. Чтобы выяснить, будут ли некоторые числа взаимно простыми, нужно найти их наибольший общий делитель и сделать вывод на основании его сравнения с единицей.
Условие: определите, являются ли числа 331 , 463 и 733 взаимно простыми.
Решение
Сверимся с таблицей простых чисел и определим, что все три этих числа в ней есть. Тогда их общим делителем может быть только единица.
Ответ: все эти числа будут взаимно простыми по отношению друг к другу.
Условие: приведите доказательство того, что числа − 14 , 105 , − 2 107 и − 91 не являются взаимно простыми.
Решение
Начнем с выявления их наибольшего общего делителя, после чего убедимся, что он не равен 1 . Поскольку у отрицательных чисел те же делители, что и у соответствующих положительных, то НОД ( − 14 , 105 , 2 107 , − 91 ) = НОД ( 14 , 105 , 2 107 , 91 ) . Согласно правилам, которые мы привели в статье о нахождении наибольшего общего делителя, в данном случае НОД будет равен семи.
Ответ: семь больше единицы, значит, взаимно простыми эти числа не являются.




























