Линейные пространства

Топологическая структура

Если (V, ‖ · ‖) — нормированное векторное пространство, норма ‖ · ‖ индуцирует метрику (понятие расстояния) и, следовательно, топология на V. Эта метрика определяется естественным образом: расстояние между двумя векторами u и v задается как ‖ u− v‖. Эта топология как раз и является самой слабой топологией, которая делает · ‖ непрерывной и совместима с линейной структурой V в следующем смысле:

Векторное сложение +: V × V → V совместно непрерывно относительно этой топологии. Это непосредственно следует из неравенства треугольника .
. Скалярное умножение ·: K × V → V, где K — скалярное поле, лежащее в основе V, совместно непрерывно. Это следует из неравенства треугольника и однородности нормы.

Аналогично, для любого полунормированного векторного пространства мы можем определить расстояние между двумя векторами u и v как ‖ u− v‖

Это превращает полунормированное пространство в псевдометрическое пространство (обратите внимание, что оно слабее, чем метрика) и позволяет определять такие понятия, как непрерывность и сходимость. Говоря более абстрактно, каждое полунормированное векторное пространство является топологическим векторным пространством и, таким образом, несет в себе топологическую структуру , индуцированную полунормой

Особый интерес представляют полные нормированные пространства, называемые банаховыми пространствами. Каждое нормированное векторное пространство V является плотным подпространством внутри банахова пространства; это банахово пространство по существу однозначно определяется V и называется пополнением V.

Две нормы в одном векторном пространстве называются эквивалентными, если они определяют одну и ту же топологию. В конечномерном векторном пространстве все нормы эквивалентны, но это неверно для бесконечномерных векторных пространств.

Все нормы в конечномерном векторном пространстве эквивалентны с топологической точки зрения, поскольку они индуцируют одну и ту же топологию (хотя результирующие метрические пространства не обязательно должны быть одинаковыми). А поскольку любое евклидово пространство полно, мы можем заключить, что все конечномерные нормированные векторные пространства являются банаховыми пространствами. Нормированное векторное пространство V локально компактно тогда и только тогда, когда единичный шар B = {x: ‖x‖ ≤ 1} компактный, что имеет место тогда и только тогда, когда V конечномерна; это следствие леммы Рисса. (На самом деле верен более общий результат: топологическое векторное пространство локально компактно тогда и только тогда, когда оно конечномерно. Дело в том, что мы не предполагаем, что топология исходит из нормы.)

Топология полунормированного векторного пространства имеет много хороших свойств. Учитывая систему соседства N (0) {\ displaystyle {\ mathcal {N}} (0)}около 0, мы можем построить все другие системы соседства как

N (Икс) знак равно Икс + N (0): знак равно {Икс + N ∣ N ∈ N (0)} {\ Displaystyle {\ mathcal {N}} (х) = х + {\ mathcal {N}} (0) : = \ {x + N \ mid N \ in {\ mathcal {N}} (0) \}}

x + N: = {x + n ∣ n ∈ N} {\ displaystyle x + N: = \ {x + n \ mid n \ in N \}}.

Более того, существует базис окрестности для 0, состоящий из поглощающего и выпуклого устанавливает. Поскольку это свойство очень полезно в функциональном анализе, обобщения нормированных векторных пространств с этим свойством изучаются под названием локально выпуклые пространства.

Линейная алгебра

Пытаясь понять, что называется вектором, нужно сначала разобраться с математическими основами. Математика – это наука, которая занимается изучением абстрактных объектов и их взаимосвязей. С ее помощью можно производить различные операции: сложение, вычитание, деление, умножение. Математика берет вещественный мир и изучает его абстрактные свойства.

Внутри этой науки имеется алгебра. Простым языком – это когда вместо чисел подставляются буквы и изучаются еще более абстрактные свойства объектов. Пример:

a + b = c;
a = c — b.

Неизвестно, какие именно цифры стоят на месте a, b, или c, но уже имеется абстрактный закон, подтвержденный практикой.

Внутри алгебры имеется линейная алгебра – она будет заниматься изучением векторных пространств и иных абстрактных понятий, которые относятся к некоторым упорядоченным данным. Примеры – координаты ракеты в космосе, пиксели на картинке, биржевые котировки.

Все указанные варианты – это примеры упорядоченных данных, которые могут быть описаны при помощи специальных элементов. Они называются векторами. Именно их изучением занимается линейная алгебра.

Конечномерные пространства

конечномерным

основную теорему о линейной
зависимости

Масштабирование одного из векторов базиса. Возьмём какое-нибудь число
и умножим на него какой-нибудь вектор . Полученная система
векторов будет базисом
наравне с прежней. Почему? Потому что любой вектор пространства по-прежнему
будет представим в виде линейной комбинации этих векторов, и по-прежнему
единственным образом. Действительно, пусть в старом базисе произвольный
вектор представлялся в виде

Тогда в новом базисе он будет представляться в виде

где . И представление это по-прежнему единственно, ведь будь
их два, представлений в исходном базисе тоже было бы два (достаточно было бы
умножить -е коэффициенты этих двух представлений на , чтобы получить
коэффициенты двух представлений того же самого вектора в старом базисе).
Прибавление к одному из векторов базиса другого, умноженного на число.
Возьмём какое-нибудь число (теперь никто не запрещает ему быть нулём,
хотя случай с нулём тривиален и неинтересен) и вместо вектора
«подсунем» в базис вектор , остальные векторы оставив
без изменения. Новая система векторов
тоже будет базисом.
Проверим это. Пусть какой-либо вектор представлялся в старом базисе в
виде

Тогда в новом базисе он примет вид

Это несложно проверить, подставив вместо сумму ,
раскрыв пару скобок и сократив пару слагаемых. Совершенно аналогично можно
получить представление вектора в прежнем базисе, зная представление в
новом. Значит, представление в новом базисе всегда существует и всегда
единственно, как и представление в прежнем базисе.
Перестановка двух векторов базиса местами. Ну тут всё очевидно.

основную теорему о
линейной зависимостив любом конечномерном линейном пространстве
все базисы состоят из одного и того же количества векторов

нулевые

если
есть некоторый базис из векторов, то никакого базиса из векторов
существовать не может

основная теорема о линейной зависимости

размерностью

Свойства орта вектора

Важным свойством орта вектора является то, что он ортогонален всем остальным векторам в той же системе координат. Это означает, что скалярное произведение орта вектора на любой другой вектор равно нулю.

Орт вектора также имеет направление, которое определяется его координатами в системе координат. Направление орта можно определить с помощью векторной операции – нормализации. Нормализация вектора заключается в делении его на его длину, что приводит к получению вектора единичной длины.

Орт вектора является важным инструментом векторной алгебры и находит применение в различных областях науки и техники. Он используется для нахождения углов между векторами, нахождения проекций векторов на плоскости и других задач.

Ортогональность орта вектора

Один из важных свойств орта вектора — его ортогональность. Два орта вектора считаются ортогональными, если их скалярное произведение равно нулю. Скалярное произведение ортогональных ортов векторов равно нулю потому, что они направлены перпендикулярно друг другу.

Ортогональность орта вектора имеет важное значение во многих областях науки и техники. Например, в компьютерной графике орты вектора используются для задания направления освещения, что позволяет создавать реалистичные изображения

Ортогональность орта вектора также используется в линейной алгебре для определения ортогональной системы векторов, которая имеет множество приложений в физике, математике и инженерии.

Важно понимать, что ортогональность орта вектора определяется только для трехмерного пространства. В двухмерном пространстве орты вектора всегда параллельны друг другу и не могут быть ортогональными

Ортогональность орта вектора — это важное понятие в линейной алгебре и визуализации данных, которое позволяет определить взаимное расположение векторов в пространстве и использовать их для решения различных задач

Нормирование орта вектора

Для нормирования орта вектора необходимо вычислить длину вектора и разделить каждую компоненту на эту длину. Таким образом, получается вектор с длиной, равной единице, и оригинальным направлением.

Формула для нормирования орта вектора выглядит следующим образом:

где — нормализованный орт вектора, — исходный вектор, — длина вектора.

Нормированный орт вектора часто используется в различных областях, таких как компьютерная графика, машинное обучение и физика, где важно иметь единичный вектор с определенным направлением для проведения вычислений или анализа данных

L1 Norm

The L1 norm also known as the taxi-cab norm or the Manhattan norm. Is another common way to normalize vectors. The formula is given below:

$||\vec{v}||_1 =\Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^1\Big)^{\frac{1}{1}}$

It may be slightly perplexing why the $\frac{1}{1}$ exponent has been included in the formula above. However, it will soon become clear. Note that we could just as easily have written the formula above as:

$||\vec{v}||_1 = \sum\limits_{i=1}^{n}|\vec{v}_i| $

Python function for L1 norm

Example

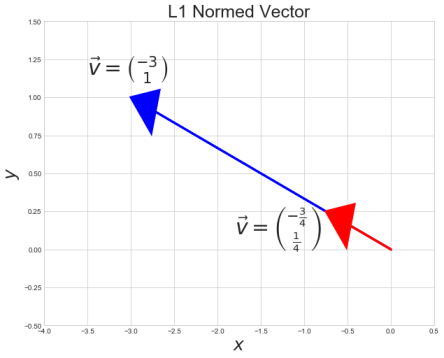
Take the following vector $\vec{v}$

$\vec{v} = \begin{bmatrix} -3 \\ 1 \\ \end{bmatrix} \hspace{0.5cm} $

Take the L1 norm

$||\vec{v}||_1 = (|x|^1 + |y|^1)^\frac{1}{1} = |x| + |y|$

$4 = |-3| + |1|$

Normalize the vector by the L1 norm

$\hat{v} = \begin{bmatrix} \frac{3}{( |-3|+|1|)} \\ \frac{3}{( |-3|+|1|)} \\ \end{bmatrix} = \begin{bmatrix} \frac{-3}{4} \\ \frac{1}{4} \\ \end{bmatrix} $

Check the L1 norm of the resulting vector equals 1

$|x| + |y| =1$

$|-\frac{3}{4}| + |\frac{1}{4}| = \frac{4}{4} = 1$

What does that look like?

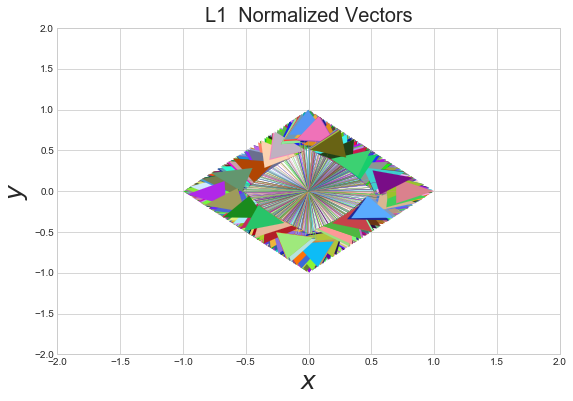
Let’s normalize the random vectors we created at the beginning of the document using the L1 norm and inspect the resulting shape.

As with the L2 norm we see an nice shape emerge after normalizing the vectors. Whereas the L2 norm vectors produced a circle, the L1 shows a diamond.

What can we say about the L1 norm?

1) The L1 norm will always be greater than or equal to the L2 norm. Why? Think back to the fact that the L1 norm is also known as the taxicab norm, we could think of the L2 norm as the as the crow flies distance, whereas the L1 norm is equivalent to taking a taxi along streets that requires turns.

2) When we normalize a 2d vector by the L1 norm. The resulting vector’s elements $|x| + |y| = 1$

3) When thinking of the L1 norm in 2d we should think of a diamond

In this section we will compare the formulae for the L1 and L2 norm. Recall the formula for the L1 norm for which a seemingly unnecessary exponents were included. Observe the formulae for the L1 and L2 norm below:

$||\vec{v}||_1 = \Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^1\Big)^{\frac{1}{1}} \\ ||\vec{v}||_2 = \Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^2\Big)^{\frac{1}{2}} \\ $

You may notice a pattern. Although Let’s add one more to show the pattern:

$||\vec{v}||_3 = \Big(\sum\limits_{i=1}^{n}|\vec{v}_i|^3\Big)^{\frac{1}{3}} \\ $

Линейная независимость

Базисом множества называется набор векторов, через линейную комбнацию которых единственным способом можно выразить все вектора этого множества и только их.

Базисы есть не только в линейной алгебре. Например, $\{1, x, x^2\}$ является базисом всех квадратных трёхчленов. Или $\{\neg, \land, \lor\}$ является базисом всех логических выражений (то есть всё можно выразить через И, ИЛИ и НЕ). В произвольном языке программирования можно выделить какой-то набор команд, через который можно будет написать всё что угодно, и он тоже в этом смысле будет базисом.

Система векторов $\{a_1, a_2, \dots, a_n\}$ называется линейно зависимой, если существует такой набор действительных коэффициентов $(\lambda_1, \lambda_2, \dots, \lambda_n)$, что $\lambda_j \neq 0$ хотя бы для одного $j$ и $\lambda_1 \cdot a_1 + \lambda_2 \cdot a_2 + \dots + \lambda_n \cdot a_n = 0$. В противном случае система называется линейно независимой. Например, базис $N$-мерного пространства — это линейно независимый набор из $N$ векторов. (Доказательство: пусть базис линейно зависим. Тогда вектор нулевой длины можно выразить хотя бы двумя способами)

Два столбца (или две строки) матрицы называются линейно зависимыми, если два образованных ими вектора являются линейно зависимыми (коллинеарными). Рангом матрицы $rang$ $A$ называется максимальное число $r$ такое, что можно выбрать $r$ попарно линейно независимых столбцов или строк в матрице.

Действия с векторами. Коллинеарность векторов

В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др. Для затравки повторим два правила, которые особенно актуальны для решения задач аналитической геометрии.

Правило сложения векторов по правилу треугольников

Рассмотрим два произвольных ненулевых вектора и :

Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор от конца вектора :

Суммой векторов и является вектор . Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору , а затем по вектору . Тогда сумма векторов представляет собой вектор результирующего перемещения с началом в точке отправления и концом в точке прибытия. Аналогичное правило формулируется для суммы любого количества векторов. Как говорится, тело может пройти свой путь сильно поддатым по зигзагу, а может и на автопилоте – по результирующему вектору суммы.

Кстати, если вектор отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.

Умножение вектора на число

Сначала о коллинеарности векторов. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Грубо говоря, речь идёт о параллельных векторах. Но применительно к ним всегда используют прилагательное «коллинеарные».

Представьте два коллинеарных вектора. Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленными. Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены.

Обозначения: коллинеарность векторов записывают привычным значком параллельности: , при этом возможна детализация: (векторы сонаправлены) или (векторы направлены противоположно).

Произведением ненулевого вектора на число является такой вектор , длина которого равна , причём векторы и сонаправлены при и противоположно направлены при .

Правило умножения вектора на число легче понять с помощью рисунка: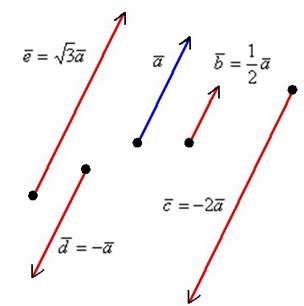

Разбираемся более детально:

1) Направление. Если множитель отрицательный, то вектор меняет направление на противоположное.

2) Длина. Если множитель заключен в пределах или , то длина вектора уменьшается. Так, длина вектора в два раза меньше длины вектора . Если множитель по модулю больше единицы, то длина вектора увеличивается в раз.

3) Обратите внимание, что все векторы коллинеарны, при этом один вектор выражен через другой, например,. Обратное тоже справедливо: если один вектор можно выразить через другой, то такие векторы обязательно коллинеарны

Таким образом: если мы умножаем вектор на число, то получится коллинеарный (по отношению к исходному) вектор.

4) Векторы сонаправлены. Векторы и также сонаправлены. Любой вектор первой группы противоположно направлен по отношению к любому вектору второй группы.

Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Усиление взаимосвязей между переменными

Взаимосвязи между переменными играют важную роль в анализе данных и машинном обучении. Более сильные и значимые взаимосвязи позволяют получить более точные и надежные результаты. В этом разделе разберем несколько способов усиления взаимосвязей между переменными.

1. Корреляционный анализ

Корреляционный анализ позволяет определить степень взаимосвязи между двумя переменными. Для этого используется коэффициент корреляции, который может принимать значения от -1 до 1. Значение 1 означает положительную линейную взаимосвязь, -1 — отрицательную линейную взаимосвязь, а 0 — отсутствие линейной взаимосвязи.

2. Преобразование переменных

Иногда преобразование переменных может помочь усилить взаимосвязи между ними. Например, можно применить логарифмическое преобразование, чтобы сгладить асимметричные распределения данных или уменьшить влияние выбросов.

3. Создание новых переменных

Создание новых переменных на основе существующих также может помочь улучшить взаимосвязи между переменными. Например, можно создать переменную, равную произведению двух других переменных, если есть предположение о существовании нелинейной зависимости.

4. Разделение данных

Иногда разделение данных на подвыборки может помочь выявить более сильные взаимосвязи. Например, можно разделить данные на две группы в зависимости от какого-то фактора и проанализировать взаимосвязи внутри каждой группы.

5. Использование дополнительных источников данных

Если взаимосвязи между переменными не оказываются достаточно сильными, можно обратиться к дополнительным источникам данных. Например, можно исследовать доступные статистические данные, опросы или провести эксперимент, чтобы получить дополнительную информацию о взаимосвязях между переменными.

Вывод

Усиление взаимосвязей между переменными может помочь улучшить точность и надежность анализа данных. Корреляционный анализ, преобразование переменных, создание новых переменных, разделение данных и использование дополнительных источников данных — это некоторые из способов усиления взаимосвязей

Важно учитывать контекст и специфику задачи при выборе и применении этих методов

Определение вектора и его роль в математике и физике

Вектор является одним из основных понятий в математике и физике. Он представляет собой величину, которая имеет не только численное значение, но и направление. Вектор может быть представлен как стрелка, направление которой указывает на направление вектора, а длина стрелки — на величину вектора.

Векторы используются для описания и решения широкого спектра задач в различных областях науки, включая физику, математику, инженерию и компьютерную графику. Они являются важным инструментом для моделирования и анализа различных физических и математических явлений.

Векторы могут быть складываться и вычитаться друг из друга, умножаться на число, а также выполнять другие операции. Их свойства позволяют определять их сумму, разность, угол между векторами, проекцию и многое другое. Векторы также удобно представлять в матричном виде, что позволяет использовать их в различных математических операциях.

В физике, векторы используются для описания физических величин, которые имеют как величину, так и направление. Например, вектор скорости описывает скорость движения тела и включает в себя информацию о его направлении. Вектор силы указывает на направление и величину силы, действующей на объект.

В математике, векторы используются для решения геометрических задач, анализа данных, решения линейных уравнений и многих других задач. Они играют важную роль в линейной алгебре, геометрии и векторном анализе.

Изучение векторов является неотъемлемой частью программы математического и физического образования. Понимание и использование векторов позволяет анализировать и решать сложные проблемы, связанные с движением, силами, силовыми полями, построением и разложением векторов и многими другими задачами.

Связь с собственными числами

Теорема . Для спектра $ \{\lambda_1,\dots,\lambda_n\} $ квадратной матрицы $ A \in \mathbb R^{n\times n} $ имеют место неравенства

$$ \sqrt{\sum_{j=1}^n |\lambda_j|^2} \le \|A\|_{_F} ; $$

$$ \sqrt{\sum_{j=1}^n | \mathfrak{Re} (\lambda_j)|^2} \le \left\|\frac{1}2(A+A^{\top})\right\|_{_F} ; $$

$$ \sqrt{\sum_{j=1}^n | \mathfrak{Im} (\lambda_j)|^2} \le \left\|\frac{1}2(A-A^{\top})\right\|_{_F} . $$

Источники

Гантмахер Ф.Р. Теория матриц. 4-е изд. М.Наука. 1988.

Беллман Р. Введение в теорию матриц. М.Наука. 1969.

(англ.) norm

(англ.) Matrix norm induced by a vector norm

(англ.) spectral norm

Зависимость векторов и свойства

В линейной алгебре вводится такое понятие, как векторная система. Под ней понимают заданный набор вида a1, a2, …, an. Если в это множество вести свободные коэффициенты, а векторные элементы системы сложить между собой, то получится выражение, являющееся линейной комбинацией рассматриваемого пространства: Ya1 + Ya2 + … + Yan.

Когда все свободные члены системы одновременно равняются нулю, то комбинация называется тривиальной. Но если хотя бы один из коэффициентов отличен от нуля, то множество уже будет нетривиальным. Например, система 0 * a1 + 0 * a2 — тривиальная, a 12 * a1 + 0 * a2 — нетривиальная. Разобравшись в этих терминах, можно дать определение зависимости системы. Так, она может быть двух типов:

линейно независимая — когда тривиальная комбинация совпадает с нулевым отрезком;
линейно зависимая — когда одна из нетривиальных комбинаций равняется нулевому отрезку.

Определение зависимости важно в векторной алгебре. Опираясь на него, исследуют размерность и базис пространства

Пусть имеется упорядоченная совокупность действительных или комплексных чисел a1, a2, … ap. Линейная комбинация будет выглядеть следующим образом: u * a1 + u * a2 + … + u * ap. Используя правила сложения и произведения векторов, а также понятие n-мерного массива, справедливо утверждать, что рассматриваемая линейная совокупность будет равняться некому отрезку: u * a1 + u * a2 + … + u * ap = b.

При исследовании системы на зависимость необходимо выполнить её проверку на достаточность признаков. Для этого вначале следует убедиться в том, что число векторов не превышает величины координат (в ином случае делается вывод о линейности), затем проверить систему на содержание нулевых отрезков. Если их нет, то необходимо составить матрицу, строками которой будут уравнения системы. При ранге составленной матрицы меньше p — система линейно зависима.

Свойства зависимых и независимых линейных отрезков:

Система, содержащая нулевую линию, является линейно зависимой.
Два одинаковых вектора в системе приводят её к линейной зависимости.
Если в пространстве существуют два пропорциональных отрезка, то она считается линейно зависимой.
Система из ограниченных прямых будет только тогда линейно зависимой, когда хотя бы один из отрезков является линейной комбинацией остальных.
Когда к линейно независимой системе присоединяется отрезок и она превращается в линейно зависимую, то добавляемый вектор можно разложить по существующим прямым системы и только единственным образом.

устои

Векторная алгебра возникла из изучения кватернионов (расширение действительных чисел) 1, i, j и k, а также декартовой геометрии, предложенной Гиббсом и Хевисайдом, которые поняли, что векторы будут служить инструментом для представляют различные физические явления.

Векторная алгебра изучается через три основы:

геометрически

Векторы представлены линиями, которые имеют ориентацию, а такие операции, как сложение, вычитание и умножение на действительные числа, определяются с помощью геометрических методов..

аналитически

Описание векторов и их операций выполняется с помощью чисел, называемых компонентами. Этот тип описания является результатом геометрического представления, потому что используется система координат.

аксиоматически

Описание векторов производится независимо от системы координат или любого типа геометрического представления..

Изучение фигур в пространстве осуществляется через их представление в системе отсчета, которая может быть в одном или нескольких измерениях. Среди основных систем:

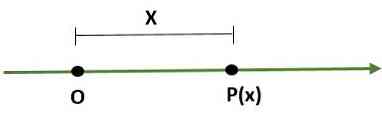
— Одномерная система, представляющая собой линию, в которой одна точка (O) представляет начало координат, а другая точка (P) определяет масштаб (длину) и ее направление:

— Прямоугольная система координат (двумерная), которая состоит из двух перпендикулярных линий, называемых осью x и осью y, которые проходят через точку (O) начала координат; таким образом, плоскость делится на четыре области, называемые квадрантами. В этом случае точка (P) на плоскости задается расстояниями, которые существуют между осями и P.

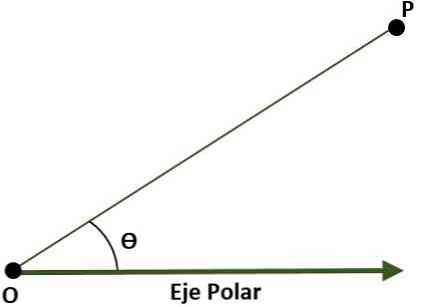
— Полярная система координат (двумерная). В этом случае система состоит из точки O (начала координат), которая называется полюсом, и луча с началом координат O, называемого полярной осью. В этом случае точка P плоскости, относительно полюса и полярной оси, задается углом (Ɵ), который образован расстоянием между началом координат и точкой P.

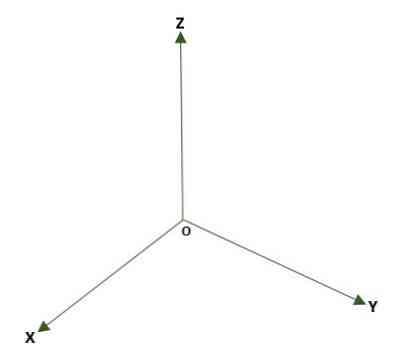
— Прямоугольная трехмерная система, образованная тремя перпендикулярными линиями (x, y, z), которые имеют точку начала O в пространстве. Формируются три координатные плоскости: xy, xz и yz; пространство будет разделено на восемь областей, называемых октантами. Ссылка на точку P пространства задается расстояниями, которые существуют между плоскостями и P.

Матрицы

Можно показать, что любую линейную функцию $f: \mathbb{R}^n \to \mathbb{R}^m$ можно представить в следующем виде:

Матрицы ввели просто как очень компактную запись этих коэффициентов $a_{ij}$.

Каждой линейной функции $f$ из $\mathbb{R}^n$ в $\mathbb{R}^m$ соответствует какая-то матрица $A$ размера $n \times m$ (первое число это количество строк, второе — столбцов) и наоборот. Элемент на пересечении $i$-ой строки и $j$-го столбца будем обозначать $A_{ij}$. Не перепутайте.

Если вектор — это упорядоченный набор скаляров, то матрицу можно рассматривать как вектор векторов. Вектор, в частности, можно представить как матрицу, у которой одна из размерностей равна единице — тогда его называют вектор-столбец либо вектор-строка.

Ещё есть тензоры — ими называют все объекты ещё более высокого порядка: векторы матриц (трёхмерный тензор), матрицы матриц (четырёхмерный тензор) и векторы матриц матриц и так далее.

У тензоров есть своя интересная алгебра, но в контекстах, в которых с ними сталкивается обычный программист, никакая алгебра, как правило, не подразумневается, и этот термин используется лишь потому, что в словосочетании «многомерный массив» слишком много букв.

Матричное умножение

Пусть линейной функции $f$ соответствует матрица $A$, а функции $g$ соответствует матрица $B$. Тогда композиции этих функций $h = f \circ g$ будет соответствовать произведение $C$ матриц $A$ и $B$, определяемое следующим образом:

Читатель может убедиться в этом, расписав, какие коэффициенты получаются, если формулы из $g$ подставить в $f$.

При перемножении матриц руками удобно думать так: элемент на пересечении $i$-го столбца и $j$-той строки — это скалярное произведение $i$-той строки $A$ и $j$-того столбца $B$. Заметим, что это накладывает ограничение на размерности перемножаемых матриц: если первая матрица имеет размер $n \times k$, то вторая должна иметь размер $k \times m$, то есть «средние» размерности обязательно должны совпадать.

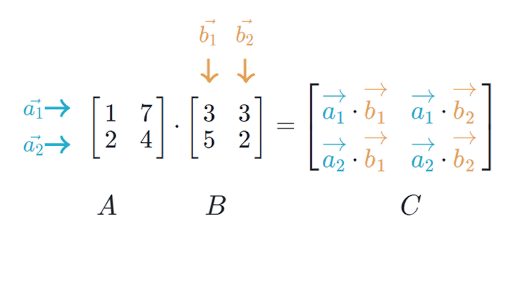
Исходное выражение для $f(x)$ теперь можно компактно записать как $f(x) = Ax$ вместо $m$ уравнений с $n$ слагаемыми в каждом.

Напишем функцию, реализующую матричное умножение:

Такая реализация хоть и наиболее простая, но не оптимальная ввиду особенностей работы кэша (см. раздел «Оптимизации матричного умножения»).

Свойства матриц

К матрицам не нужно относиться как к табличкам, в которых стоят какие-то числа. Каждой матрице соответствует какая-то линейная функция, как-то преобразующая вектора. Центральными объектами линейной алгебры являются именно линейные функции, а не матрицы.

Благодаря этому взаимно однозначному соотношению все ранее упомянутые свойства линейных функций переносятся и на матрицы:

Сумма матриц $A$ и $B$ тоже является матрицей: $C = A+B: \; C_{ij} = A_{ij} + B_{ij}$.
Сумма матриц коммутативна: $A+B = B+A$.
Сумма матриц ассоциативна: $(A+B)+C = A+(B+C)$.
Умножение матриц ассоциативно: $(AB)C = A(BC) = ABC$.
Умножение матриц в общем случае не коммутативно.

Есть специальная матрица $I$ (иногда обозначается $E$), которая называется единичной и относительно умножения ничего не делает, то есть ведёт себя как единица. У неё единицы на главной диагонали и нули вне неё:

Некоторые линейные функции обратимы (например, поворот на угол), некоторые — необратимы (например, проекция). Понятие обратимости можно продолжить и на матрицы.

Определение. Матрица $A$ является обратимой, если существует матрица $A^{-1}$ такая, что $A \cdot A^{-1} = A^{-1} \cdot A = I$.

Из формулы следует, что матрица $A$ должна быть квадратной, но этого не всегда достаточно. У неквадратных матриц обратных матриц не существует. Обратную матрицу можно находить за $O(n^3)$ методом Гаусса, который будет рассмотрен чуть позже.

Примеры матриц

Матрица «увеличь всё в два раза»:

Матрица «поменяй $x$ и $y$ местами»:

Матрица поворота на угол $\alpha$ на плоскости:

Матрица проецирования на плоскость $xy$ в трёхмерном пространстве:

Особенности длины вектора

Особенности длины вектора включают:

Положительность: длина вектора всегда является положительным числом или нулем. Даже если вектор направлен в обратную сторону, его длина будет положительной.
Зависимость от координат: длина вектора зависит от координат его начальной и конечной точки. Изменение какой-либо из этих координат приведет к изменению длины вектора.
Выражение через компоненты: длину вектора можно выразить через компоненты вектора с использованием теоремы Пифагора в трехмерном пространстве или теоремы Пифагора для произвольных размерностей.
Соотношение скалярного произведения: длина вектора может быть выражена через скалярное произведение самого вектора на себя.

Определение и измерение длины вектора являются важными векторными операциями и широко используются в геометрии, физике и других науках. Знание особенностей длины вектора позволяет более полно понять его свойства и использовать векторные операции для решения различных задач.

Модуль или абсолютная величина вектора

Модуль или абсолютная величина вектора представляет собой его длину, которая определяется по формуле:

Двумерный пространство:	\|a\| = √(a_x)2 + (a_y)2
Трехмерное пространство:	\|a\| = √(a_x)2 + (a_y)2 + (a_z)2

Где a_x, a_y, a_z представляют собой координаты вектора в соответствующих осях. Модуль вектора всегда является положительным числом или нулем, но никогда не может быть отрицательным.

Модуль вектора имеет важное значение при решении задач по физике и математике. Он позволяет определить длину перемещения, скорость и ускорение, а также установить равенство или неравенство между векторами

Благодаря модулю вектора можно производить его нормирование, то есть приводить вектор к единичной длине.

Модуль вектора также позволяет определить перпендикулярность двух векторов. Если модуль вектора равен нулю, значит он является нулевым вектором, который не имеет направления и считается коллинеарным любому другому вектору.

Неотрицательность длины вектора

Длина вектора определяется как квадратный корень из суммы квадратов его составляющих. Таким образом, все компоненты вектора возводятся в квадрат, суммируются, и затем из полученной суммы берется квадратный корень.

Такое определение длины вектора обладает следующими особенностями:

Квадратная корень всегда дает неотрицательное значение, даже если вектор имеет отрицательные компоненты.
Если вектор состоит из нулевых компонент, его длина будет равна нулю.
Длина вектора может быть равной нулю только в случае, когда сам вектор также равен нулевому вектору.

Таким образом, неотрицательность длины вектора является важным свойством, которое следует учитывать при работе с векторами и их длинами.

Геометрическая интерпретация длины вектора

Геометрически, длина вектора представляет собой расстояние от начала координат до конца вектора в пространстве. Она может быть вычислена с помощью формулы, которая основана на теореме Пифагора. Для двумерного пространства формула имеет вид:

|AB| = √((x2 — x1)^2 + (y2 — y1)^2)

где (x1, y1) и (x2, y2) — координаты начала и конца вектора, соответственно.

Геометрическая интерпретация длины вектора позволяет наглядно представить, насколько «длинным» или «коротким» является вектор. Она также позволяет определить направление вектора, так как длина вектора всегда положительна.

Длина вектора имеет важное значение во многих областях, включая математику, физику и компьютерную графику. Например, вектоная алгебра и геометрия используют длину вектора для определения углов между векторами и вычисления скалярных произведений

Таким образом, понимание геометрической интерпретации длины вектора является важным аспектом, позволяющим более глубоко и точно изучить свойства и особенности векторов.

Нормированные пространства как факторпространства полунормированных пространств

Определение многих нормированных пространств (в частности, Банаховы пространства ) включают полунорму, определенную на векторном пространстве, а затем нормированное пространство определяется как фактор-пространство по подпространству элементов нулевой полунормы. Например, с пробелами L функция, определенная как

‖ f ‖ p = (∫ | f (x) | pdx) 1 / p {\ displaystyle \ | f \ | _ {p } = \ left (\ int | f (x) | ^ {p} \; dx \ right) ^ {1 / p}}

— полунорма в векторном пространстве всех функций, на которых Лебег интеграл в правой части определен и конечен. Однако полунорма равна нулю для любой функции , поддерживаемой на множестве меры Лебега ноль. Эти функции образуют подпространство, которое мы «выделяем», делая их эквивалентными нулевой функции.