Синус, косинус, тангенс, котангенс

Содержание

1 Элементарные тригонометрические тождества
- 1.1 Определения
- 1.2 Тождества отношения
- 1.3 Дополнительные тождества углов
- 1.4 Пифагоровы тождества
- 1.5 Идентичность суммы углов
  - 1.5.1 Синус
  - 1.5.2 Косинус
  - 1.5.3 Тангенс и котангенс
- 1.6 Идентичность двойного угла
- 1.7 Идентичность половинного угла
- 1.8 Разное — тождество тройного касательного
- 1.9 Прочее — тождество тройного котангенса
- 1.10 Сумма тождеств продукта
  - 1.10.1 Доказательство тождеств синуса
  - 1.10.2 Доказательство тождеств косинуса
- 1.11 Неравенства
2 Идентичности, связанные с исчислением
- 2.1 Предварительные сведения
- 2.2 Идентичность синуса и углового отношения
- 2.3 Идентичность косинуса и углового отношения
- 2.4 Идентичность косинуса и квадрата углового отношения
- 2.5 Доказательство сочетания триггерного и обратного тригонометрические функции
3 См. также
4 Примечания
5 Ссылки

Формулы приведения для котангенса

ctg(π/2-α) = tg(α)
ctg(π/2+α) = -tg(α)
ctg(π-α) = -ctg(α)
ctg(π+α) = ctg(α)
ctg(3π/2-α) = tg(α)
ctg(3π/2+α) = -tg(α)
ctg(2π-α) = -ctg(α)
ctg(2π+α) = ctg(α)

Запомнить все формулы приведения достаточно непросто, ибо в них не прослеживается какой-либо явной закономерности.

Однако, это можно сделать, если понять принцип по которому в приведенной формуле происходит или не происходит смена функции на кофункцию и смена или не смена знака функции.

Когда надо менять название функции в формуле приведения?

Смена или не смена функции в формуле приведения зависит от того, к какому диаметру тригонометрического круга прилежит угол α в формуле приведения.

π/2±α и 3π/2±α — это вертикальный диаметр тригонометрического круга (ось Y), поскольку точки π/2 и π3/2 лежат на оси Y. Если помотать головой вверх-вниз, как бы скользя взглядом по оси ординат, то автоматически получим ответ на вопрос «надо ли менять название функции в формуле приведения?» — да, надо.

π±α и 2π±α — это горизонтальный диаметр тригонометрического круга (ось X), поскольку точки π и 2π лежат на оси Х. Если помотать головой влево-вправо, как бы скользя взглядом по оси абсцисс, то автоматически получим ответ на вопрос «надо ли менять название функции в формуле приведения?» — нет, не надо.

Когда надо менять знак функции в формуле приведения?

Для ответа на этот вопрос надо знать знаки функций синуса, косинуса, тангенса и котангенса в каждом квадранте тригонометрического круга.

Для синуса и косинуса — это просто, если помнить, что синус — это ордината (Y), а косинус — абсцисса (X):

sin — это ось Y или вертикальная ось, поэтому, все, что лежит выше оси абсцисс — это «плюс» (I, II квадранты), что лежит ниже — «минус» (III, IV квадранты);
cos — это ось X или горизонтальная ось, поэтому, все, что лежит правее оси ординат — это «плюс» (I, IV квадранты), что лежит левее — «минус» (II, III квадранты);
tg и ctg — это отношение синуса и косинуса, поэтому, тангенс и котангенс будут положительны в тех квадрантах, в которых синус и косинус имеют одинаковый знак — это нечетные квадранты (I, III); соответственно, в четных квадрантах тангенс и котангенс будут отрицательны.

Знак функции в формуле приведения ставится по квадранту исходного угла, при этом считаем, что сам угол α является острым.

Например, для угла π-α получается, что угол находится во II квадранте, т.к., π-α будет лежать в пределах от 90° до 180° (см. рисунок выше). Во втором квадранте синус положителен, поэтому, в формуле приведения надо будет ставить знак, идентичный знаку исходной функции, т. е., «плюс». Поскольку угол π-α прилежит к горизонтальному диаметру, то сама функция не меняется. Получается, что sin(π-α) = sin(α).

Для косинуса надо будет сменить знак, т.к., во втором квадранте косинус отрицателен: cos(π-α) = -cos(α).

Для тангенса и котангенса: в четном квадранте — знак «минус», а функция остается прежней: tg(π-α) = -tg(α); ctg(π-α) = -сtg(α).

Для угла π+α получается, что угол находится во III квадранте, т.к., π+α будет лежать в пределах от 180° до 270° (см. рисунок). В третьем квадранте синус отрицателен, поэтому, в формуле приведения надо будет сменить знак. Поскольку угол π+α прилежит к горизонтальному диаметру, то функция не меняется. Получается, что sin(π+α) = -sin(α). Аналогично для косинуса: cos(π+α) = -cos(α).

Для тангенса и котангенса: в нечетном квадранте — знак «плюс», а функция остается прежней: tg(π+α) = tg(α); ctg(π+α) = сtg(α).

Десятиминутный ролик на ЮТуб, посмотрев который, вы навсегда запомните, как легко и просто приводить углы в тригонометрических функциях:

Пример решения уравнения с помощью формул приведения:

√2·sin(13π/4)
√2·sin(3π+π/4)
√2·sin(π+π/4)
sin(π+π/4)=-sin(π4)=-√2/2
√2·(-√2/2)=-1

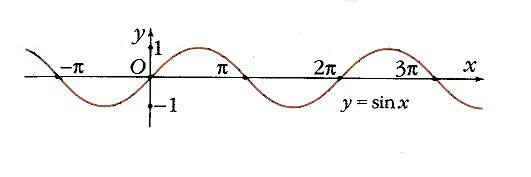
Функция y = sin х.

На единичной окружности углу x
0 соответствует точка А
(рис. 7),а ее проекцией на ось Оу
будет точка N
. З
начение функции у 0 =
sin x 0
определяется как ордината точки А
.Точка В
(угол x
0 , у
0)принадлежит графику функции y
= sin x
(рис. 8).Ясно, что функция y =
sin x
периодическая, ее период равен 2p

sin (x
+ 2p

) = sin (x
).

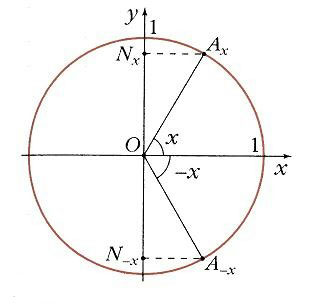
Для двух значений аргумента, х
и – ,проекции соответствующих им точек А x
и А -x
на ось Оу
расположены симметрично относительно точки О
. Поэтому

sin (–x
) = –sin (x
),

т.е. синус – функция нечетная, f(–x
) = –f(x
)(рис. 9).

Если точку A
повернуть относительно точки О
на угол p

/2 против часовой стрелки (другими словами, если угол х
увеличить на p

/2), то ее ордината в новом положении будет равна абсциссе в старом. А значит,

sin (x
+ p

/2) = cos x.

Иначе, синус – это косинус, «запоздавший» на p

/2, поскольку любое значение косинуса «повторится» в синусе, когда аргумент возрастет на p

/2. И чтобы построить график синуса, достаточно сдвинуть график косинуса на p

/2 вправо (рис. 10)

Чрезвычайно важное свойство синуса выражается равенством

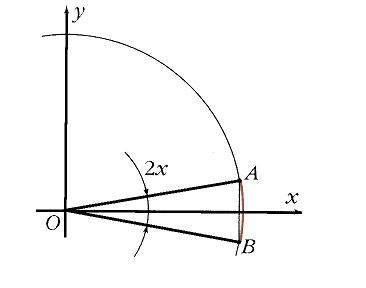
Геометрический смысл равенства виден из рис. 11. Здесь х –
это половина дуги АВ
,а sin х –
половина соответствующей хорды. Очевидно, что по мере сближения точек А
и В
длина хорды все точнее приближается к длине дуги. Из того же рисунка несложно извлечь неравенство

|sin x
| x|, верное при любом х
.

Формулу (*) математики называют замечательным пределом. Из нее, в частности, следует, что sin х
»
х
при малых х
.

Функции у
= tg х, у
= ctg х
.
Две другие тригонометрические функции – тангенс и котангенс проще всего определить как отношения уже известных нам синуса и косинуса:

Как синус и косинус, тангенс и котангенс – функции периодические, но их периоды равны p

, т.е. они вдвое меньше, чем у синуса и косинуса. Причина этого понятна: если синус и косинус оба поменяют знаки, то их отношение не изменится.

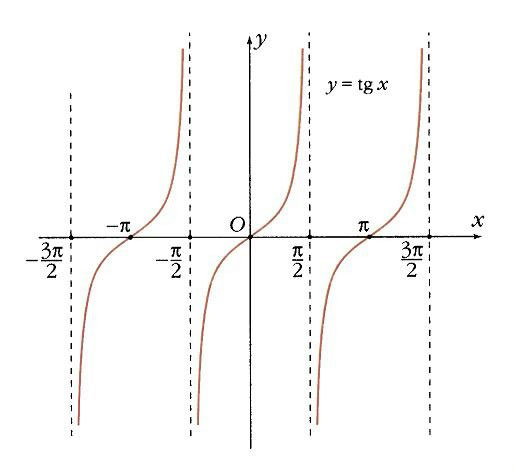
Поскольку в знаменателе тангенса находится косинус, то тангенс не определен в тех точках, где косинус равен 0, – когда х
= p

/2 + kp

.Во всех остальных точках он монотонно возрастает. Прямые х
= p

/2 + kp

для тангенса являются вертикальными асимптотами. В точках kp

тангенс и угловой коэффициент составляют 0 и 1 соответственно (рис. 12).

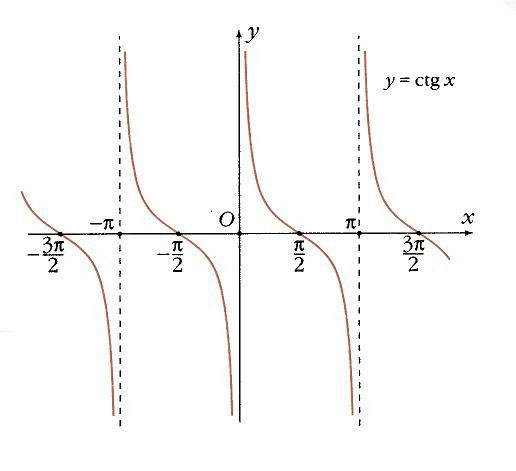
Котангенс не определен там, где синус равен 0 (когда х = kp

).В остальных точках он монотонно убывает, а прямые х = kp

–
его вертикальные асимптоты. В точках х = p

/2 + kp

котангенс обращается в 0, а угловой коэффициент в этих точках равен –1 (рис. 13).

Методы раскрытия скобок

Раскрытие скобок — это прием, который применяется в математике для упрощения выражений. Существуют различные методы раскрытия скобок, которые могут использоваться в разных ситуациях.

Метод раскрытия одной пары скобок

В этом методе мы раскрываем одну пару скобок, используя свойство дистрибутивности умножения относительно сложения или вычитания.

Рассмотрим пример:

Здесь мы умножаем каждый элемент внутри скобок на второе число и затем складываем полученные результаты.

Метод раскрытия нескольких пар скобок

В случае, когда в выражении присутствует несколько пар скобок, можно использовать метод множественного раскрытия скобок.

Рассмотрим пример:

Здесь мы раскрываем каждую пару скобок и перемножаем все элементы между собой, чтобы получить все возможные комбинации.

Метод раскрытия квадратных скобок

Если у нас есть квадратные скобки, то мы можем использовать метод дистрибутивности умножения для их раскрытия.

Рассмотрим пример:

Здесь мы умножаем каждый элемент внутри квадратных скобок на второе число и затем складываем полученные результаты.

Метод раскрытия фигурных скобок

Если у нас есть фигурные скобки, то мы можем использовать метод дистрибутивности умножения для их раскрытия.

Рассмотрим пример:

Здесь мы умножаем каждый элемент внутри фигурных скобок на второе число и затем складываем полученные результаты.

Метод раскрытия скобок с использованием квадратного корня

Если у нас имеется выражение со скобкой, в которой присутствует квадратный корень, мы можем использовать метод домножения на сопряженное значение.

Рассмотрим пример:

Здесь мы домножаем каждый элемент внутри скобок на соответствующее значение и затем складываем полученные результаты.

В зависимости от конкретной ситуации и типа скобок, необходимо выбирать соответствующий метод раскрытия скобок. Эти методы являются базовыми и могут быть дополнены или комбинированы для решения более сложных задач.

Тангенс угла

Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:

Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):

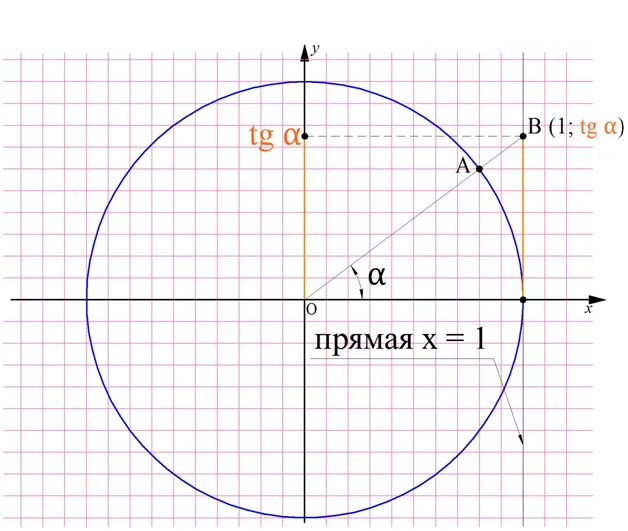
Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:

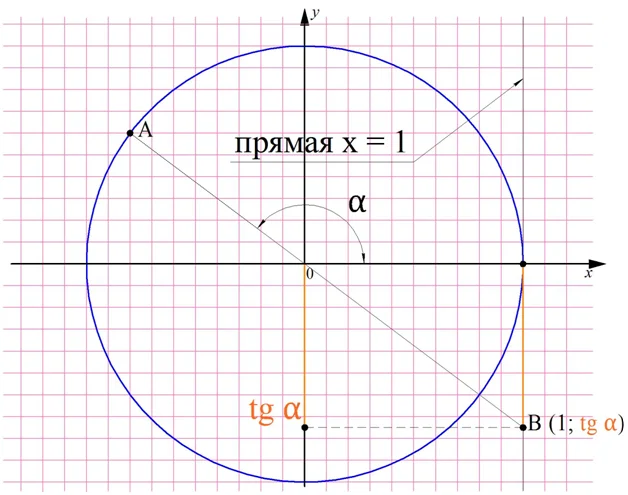
С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:

Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:

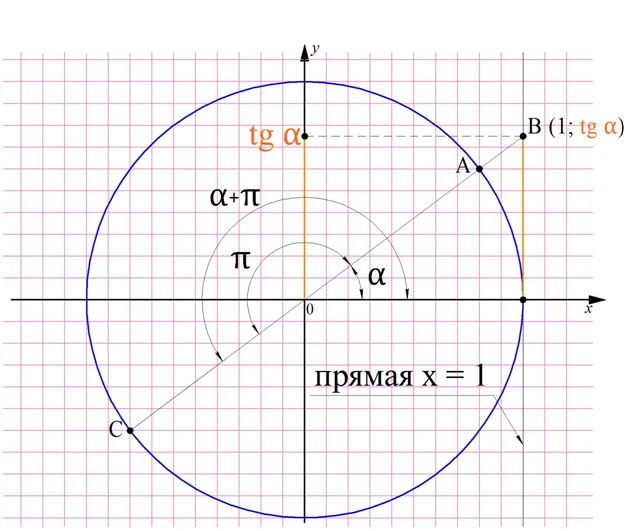
Это значит, что справедлива формула:

tg(α + π) = tg α

С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:

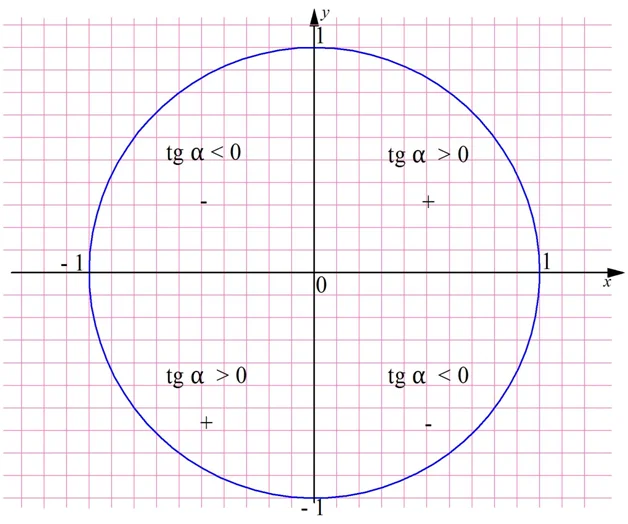
Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):

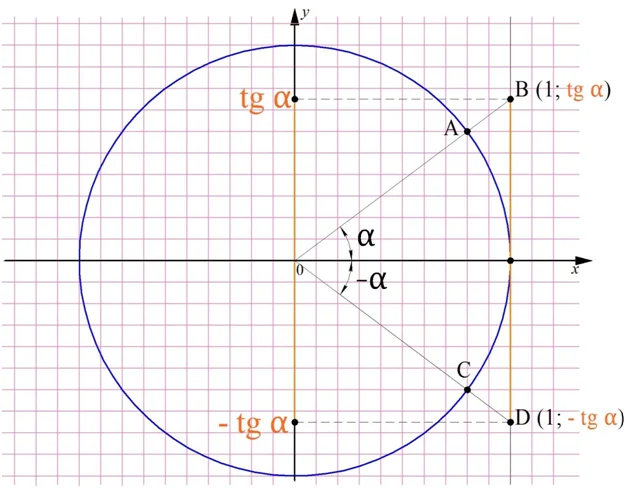
Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.

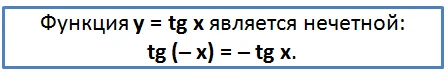
Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:

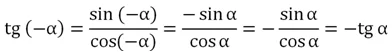
Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:

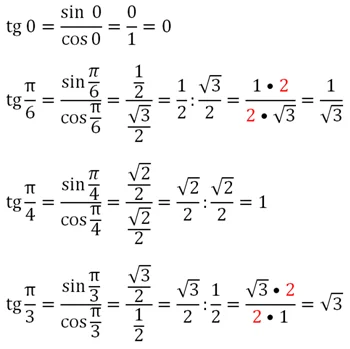
Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.

Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.

В частности, тангенс не определен при х = – π/2.

Косинус в квадрате, синус в квадрате

Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.

Для их вычисления следует запомнить основное тригонометрическое тождество:

sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).

Из тригонометрического тождества делаем выводы о синусе:

sin 2 α = 1 — cos 2 α

или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.

sin 2 α = (1 – cos(2α)) / 2

Из тригонометрического тождества делаем выводы о косинусе:

cos 2 α = 1 — sin 2 α

или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.

cos 2 α = (1 + cos(2α)) / 2

Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.

Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание

Добавить интересную новость

Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников

user->isGuest) »]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], ) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else user->identity->profile->first_name) || !empty(\Yii::$app->user->identity->profile->surname))user->identity->profile->first_name . ‘ ‘ . \Yii::$app->user->identity->profile->surname; > else echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>

При правильном ответе Вы получите 8 баллов

Упростить выражение с квадратом косинуса:

Выберите всего один правильный ответ.

Добавление комментариев доступно только зарегистрированным пользователям

Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.

28.01.17 / 22:14, Иван ИвановичОтветить -2

Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.

28.01.17 / 22:14, Иван Иванович Ответить +5

Источник

Область применения

Для того чтобы найти значение тригонометрических функций, берётся окружность на оси координат, у которой радиус равен единице, а диаметры у неё находятся в перпендикулярном положении.

Для такого вычисления нам понадобится отложить от точки, которая принадлежит окружности различные дуги, любой длины. Соответственно если мы отложим их против часовой стрелки они примут положительное значение, а если по часовой, то отрицательное.

Допустим конец дуги имеет некую длину s, в таком случае проекция радиуса в любом выбранном значении диаметра станет значением косинуса данной дуги. Выбранная длина s, или радианная мера угла, будет считаться числом аргумента. А если этот самый аргумент, это тригонометрическая функция угла, то мы знаем, что значение может быть и в градусах.

Мы знаем, что острый угол имеет значения больше нуля, но меньше п\2. В таком случае тригонометрическая функция рассматривается как катет делённый на гипотенузу. Такие названия сторон связаны с прямоугольным треугольником, в котором величина угла равна 90 градусов.

Чтобы решить задачи с функциями тригонометрии, используют теорему Пифагора. Такая теорема основана на свойствах того самого прямоугольного треугольника, в котором квадрат гипотенузы равен сумму квадратов катетов.

Так как дуга делит окружность на несколько частей, то мы можем увидеть, что углы лежащие в первой четверти больше нуля. А во второй синус меньше, а косинус больше нуля, а в третьей все функции будут меньше нуля, то есть отрицательными, четвёртая имеет значения противоположные второй. Не стоит забывать, что для построения окружности вам понадобится циркуль.

Как мы видим формулы двойного угла, не так трудно вывести, для этого необходимо знать основные тригонометрические тождества и разобраться в единичной окружности на оси координат. Также необходимо отметить, что формулы двойного угла, как и другие формулы тригонометрии используются в разных сферах жизни:

В астрономии, учёные с помощью формул вычисляют положение небесных тел, а также расстояние до них;
Для различного вида навигации, к примеру, морской и воздушной;
В медицине и биологии, при построении биоритма живых организмов, а также тригонометрия служит основой работы некоторой медицинской техники;
Архитекторам она важна при создании планов строений;
но и это не всё, тригонометрия важна и для экономики, в производстве и создании электроники, в различных аналитических вычислениях, акустических построениях и многом другом.

Преобразование произведения тригонометрических функций

В некотором смысле формулы произведения синуса, косинуса, тангенса и котангенса являются обратными к тригонометрическим формулам суммы и разности тригонометрических функций. При помощи этих формул возможно перейти от произведения к сумме или разности.

Для вывода нам опять понадобятся формулы косинуса суммы и разности:
$$\cos(\alpha+\beta)=\cos(\alpha)*\cos(\beta)-\sin(\beta)*\sin(\alpha);$$
$$\cos(\alpha-\beta)=\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);$$

Сложим эти две формулы. Для этого складываем их левые части и приравниваем сумме правых частей:

$$\cos(\alpha+\beta)+\cos(\alpha-\beta)=\cos(\alpha)*\cos(\beta)-\sin(\beta)*\sin(\alpha)+\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);$$
Приводим подобные слагаемые:
$$\cos(\alpha+\beta)+\cos(\alpha-\beta)=2*\cos(\alpha)*\cos(\beta);$$
Отсюда получаем:
$$\cos(\alpha)*\cos(\beta)=\frac{1}{2}*(\cos(\alpha+\beta)+\cos(\alpha-\beta));$$
Формула произведения косинусов доказана.

Произведение синусов доказывается похожим образом. Для этого домножим формулу косинуса суммы слева и справа на $(-1)$:
$$-\cos(\alpha+\beta)=-\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);$$
Косинус разности оставим без изменений:
$$\cos(\alpha-\beta)=\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);$$
Сложим опять эти две формулы:
$$\cos(\alpha-\beta)-\cos(\alpha+\beta)=\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha)-\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);$$
$$\cos(\alpha-\beta)-\cos(\alpha+\beta)=2*\sin(\beta)*\sin(\alpha);$$
$$\sin(\beta)*\sin(\alpha)=\frac{1}{2}*(\cos(\alpha-\beta)-\cos(\alpha+\beta));$$
Произведение синусов тоже доказано.

Для того, чтобы вывести формулу произведения синуса и косинуса, нам понадобятся формулы синуса суммы и разности:
$$\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);$$
$$\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);$$
Сложим их:
$$\sin(\alpha+\beta)+\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha)+\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);$$
$$\sin(\alpha+\beta)+\sin(\alpha-\beta)=2*\sin(\alpha)*\cos(\beta);$$
$$\sin(\alpha)*\cos(\beta)=\frac{1}{2}*(\sin(\alpha+\beta)+\sin(\alpha-\beta));$$

Пример 11
Вычислить $\sin(75^o)*\cos(15^o)=?$

Воспользуемся формулой произведения синуса и косинуса:
$$\sin(\alpha)*\cos(\beta)=\frac{1}{2}*(\sin(\alpha+\beta)+\sin(\alpha-\beta));$$
$$\sin(75^o)*\cos(15^o)=\frac{1}{2}*(\sin(75^o+15^o)+\sin(75^o-15^o))=$$
$$=\frac{1}{2}*(\sin(90^o)+\sin(60^o))=\frac{1}{2}*(1+\frac{\sqrt{3}}{2})=\frac{2+\sqrt{3}}{4}.$$

Определение

Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.

Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.

Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.

Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.

Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.

Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.

Power series and Taylor series

Computation of power series

We can use the identity:

sin2⁡x=1−cos⁡(2x)2{\displaystyle \!\sin ^{2}x={\frac {1-\cos(2x)}{2}}}

along with the power series for the cosine function, to find the power series for sin2{\displaystyle \sin ^{2}}.

The power series for the cosine function converges to the function everywhere, and is:

cos⁡x=1−x22!+x44!−x66!+⋯=∑k=∞(−1)kx2k(2k)!{\displaystyle \!\cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\dots =\sum _{k=0}^{\infty }{\frac {(-1)^{k}x^{2k}}{(2k)!}}}

The power series for cos⁡(2x){\displaystyle \cos(2x)} is:

cos⁡(2x)=1−(2x)22!+(2x)44!−(2x)66!+⋯=∑k=∞(−1)k22kx2k(2k)!{\displaystyle \!\cos(2x)=1-{\frac {(2x)^{2}}{2!}}+{\frac {(2x)^{4}}{4!}}-{\frac {(2x)^{6}}{6!}}+\dots =\sum _{k=0}^{\infty }{\frac {(-1)^{k}2^{2k}x^{2k}}{(2k)!}}}

The power series for 1−cos⁡(2x){\displaystyle 1-\cos(2x)} is:

1−cos⁡(2x)=(2x)22!−(2x)44!+(2x)66!−⋯=∑k=1∞(−1)k−122kx2k(2k)!{\displaystyle \!1-\cos(2x)={\frac {(2x)^{2}}{2!}}-{\frac {(2x)^{4}}{4!}}+{\frac {(2x)^{6}}{6!}}-\dots =\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}2^{2k}x^{2k}}{(2k)!}}}

Dividing by 2, we get the power series for sin2⁡x{\displaystyle \sin ^{2}x}:

sin2⁡x=21×22!−23×44!+25×66!−⋯=∑k=1∞(−1)k−122k−1x2k(2k)!{\displaystyle \!\sin ^{2}x={\frac {2^{1}x^{2}}{2!}}-{\frac {2^{3}x^{4}}{4!}}+{\frac {2^{5}x^{6}}{6!}}-\dots =\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}2^{2k-1}x^{2k}}{(2k)!}}}

Here’s another formulation with the first few terms written more explicitly:

sin2⁡x=x2−x43+2×645−…{\displaystyle \!\sin ^{2}x=x^{2}-{\frac {x^{4}}{3}}+{\frac {2x^{6}}{45}}-\dots }

Taylor polynomials as approximations

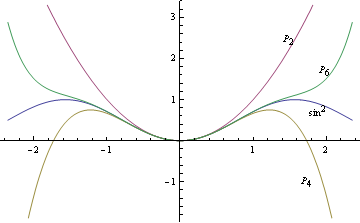
Note that since sin2{\displaystyle \sin ^{2}} is an even function, all its Taylor polynomials are also even polynomials. In the figure below, we consider the graphs of sin2{\displaystyle \sin ^{2}} and its second, fourth, and sixth Taylor approximations.

Second Taylor polynomial P2(x){\displaystyle P_{2}(x)}, which equals the third Taylor polynomial, P3(x){\displaystyle P_{3}(x)}, is x2{\displaystyle x^{2}}.
Fourth Taylor polynomial P4(x){\displaystyle P_{4}(x)}, which equals the fifth Taylor polynomial, P5(x){\displaystyle P_{5}(x)}, is x2−x43{\displaystyle x^{2}-{\frac {x^{4}}{3}}}.
Sixth Taylor polynomial, P6(x){\displaystyle P_{6}(x)}, which equals the seventh Taylor polynomial P7(x){\displaystyle P_{7}(x)}, is x2−x43+2×645{\displaystyle x^{2}-{\frac {x^{4}}{3}}+{\frac {2x^{6}}{45}}}.

Сферическая тригонометрия

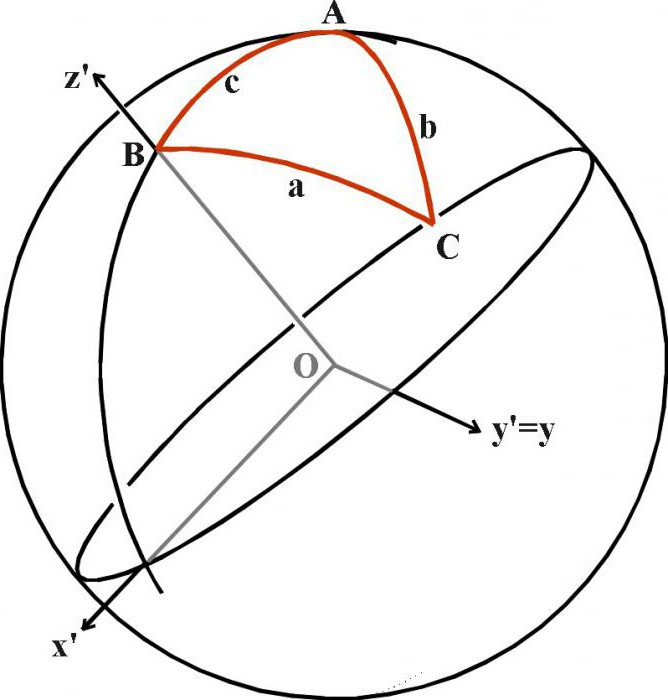
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».

Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой

Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях

Формулы суммы и разности тригонометрических функций

Синус суммы и разности:
$$\mathbf{\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);}$$
$$\mathbf{\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);}$$
Косинус суммы и разности:
$$\mathbf{\cos(\alpha+\beta)=\cos(\alpha)*\cos(\beta)-\sin(\beta)*\sin(\alpha);}$$
$$\mathbf{\cos(\alpha-\beta)=\cos(\alpha)*\cos(\beta)+\sin(\beta)*\sin(\alpha);}$$
Тангенс суммы и разности:
$$\mathbf{tg(\alpha+\beta)=\frac{tg(\alpha)+tg(\beta)}{1-tg(\alpha)*tg(\beta)};}$$
$$\mathbf{tg(\alpha-\beta)=\frac{tg(\alpha)-tg(\beta)}{1+tg(\alpha)*tg(\beta)};}$$
Котангенс суммы и разности:
$$\mathbf{сtg(\alpha+\beta)=\frac{-1+сtg(\alpha)*ctg(\beta)}{ctg(\alpha)+ctg(\beta)};}$$
$$\mathbf{сtg(\alpha-\beta)=\frac{-1-сtg(\alpha)*ctg(\beta)}{ctg(\alpha)-ctg(\beta)};}$$

Формулы суммы разности тригонометрических функций попадаются в ЕГЭ по профильной математике в №12. В прошлые года эти формулы давались в справочные материалах и учить их было не обязательно. Тем не менее, я бы рекомендовал выучить хотя бы формулы суммы и разности для синуса и косинуса.

Это не очень удобно, но иногда формулы суммы разности используют для вывода формул приведения:

Пример 3
Упростить выражение $sin(\frac{\pi}{2}+\alpha)$.

Воспользуемся формулой синуса суммы:
$$\sin(\alpha+\beta)=\sin(\alpha)*\cos(\beta)+\sin(\beta)*\cos(\alpha);$$
$$\sin(\frac{\pi}{2}+\alpha)=\sin(\frac{\pi}{2})*\cos(\alpha)+\sin(\alpha)*\cos(\frac{\pi}{2})=$$
$$=1*\cos(\alpha)+\sin(\alpha)*0=\cos(\alpha);$$

Формулы суммы разности так же полезны, когда нужно посчитать значение тригонометрических функций некоторых нестандартных углов:

Пример 4
Найдите значение $\sin(15^o)=?$

$15^o$ нестандартный угол, вы его не найдете в тригонометрической таблице углов. Представим $15^o$ в виде разности стандартных углов $15^o=45^o-30^o$. И воспользуемся формулой синуса разности:
$$\sin(\alpha-\beta)=\sin(\alpha)*\cos(\beta)-\sin(\beta)*\cos(\alpha);$$
$$\sin(15^o)=\sin(45^o-30^o)=\sin(45^o)*\cos(30^o)-\sin(30^o)*\cos(45^o)=$$
$$=\frac{\sqrt{2}}{2}*\frac{\sqrt{3}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
Вот мы наши синус $15^o$. Получилось такое иррациональное некрасивое выражение, так и оставляем.

Ответ: $\sin(15^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.$

Пример 5
Найдите значение $\cos(75^o)=?$

$75^o$ можно представить в виде суммы стандартных углов $75^o=30^o+45^o$. Здесь воспользуемся формулой косинуса суммы:
$$\cos(\alpha+\beta)=\cos(30^o)*\cos(45^o)-\sin(30^0)*\sin(45^0)=$$
$$=\frac{\sqrt{3}}{2}*\frac{\sqrt{2}}{2}-\frac{1}{2}*\frac{\sqrt{2}}{2}=$$
$$=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4};$$
У нас получился опять отвратительный ответ, но внимательный читатель заметит, что ответ такой же, как в предыдущем примере, это значит, что $\cos(75^o)=\sin(15^o)$. Такой же вывод можно было бы сделать исходя из формул приведения и знания тригонометрической окружности.

Ответ: $\cos(75^o)=\frac{\sqrt{6}-\sqrt{2}}{4}.$

Мы не будем выводить эти формулы — это не самое приятное занятие. Их проще выучить, а вывод вам вряд ли когда-либо пригодится. Но сами формулы суммы и разности служат основой для доказательства других тригонометрических формул.

Differentiation

First derivative

We have:

ddx(sin2⁡x)=sin⁡(2x){\displaystyle \!{\frac {d}{dx}}(\sin ^{2}x)=\sin(2x)}

We can do this two ways.

Using the chain rule for differentiation, we have:

ddx(sin⁡x)2=2sin⁡xddx(sin⁡x)=2sin⁡xcos⁡x{\displaystyle \!{\frac {d}{dx}}=2\sin x{\frac {d}{dx}}(\sin x)=2\sin x\cos x}

By the double angle sine formula, this is the same as sin⁡(2x){\displaystyle \sin(2x)}.

Alternatively, using the double angle cosine formula, we rewrite:

sin2⁡x=1−cos⁡(2x)2{\displaystyle \sin ^{2}x={\frac {1-\cos(2x)}{2}}}

Differentating, we get:

ddx(sin2⁡x)=−12ddx(cos⁡(2x))=−12⋅2⋅(−sin⁡(2x))=sin⁡(2x){\displaystyle \!{\frac {d}{dx}}(\sin ^{2}x)={\frac {-1}{2}}{\frac {d}{dx}}(\cos(2x))={\frac {-1}{2}}\cdot 2\cdot (-\sin(2x))=\sin(2x)}

Second derivative

Differentiating the derivative again, we get:

d2dx2(sin2⁡x)=ddxsin⁡(2x)=dd(2x)sin⁡(2x)d(2x)dx=2cos⁡(2x){\displaystyle {\frac {d^{2}}{dx^{2}}}(\sin ^{2}x)={\frac {d}{dx}}={\frac {d}{d(2x)}}{\frac {d(2x)}{dx}}=2\cos(2x)}

Четность и периодичность.

Функция называется четной, если f
(–x
) = f
(x
). Функции косинус и секанс – четные, а синус, тангенс, котангенс и косеканс – функции нечетные:

sin (–α) = – sin α	tg (–α) = – tg α
cos (–α) = cos α	ctg (–α) = – ctg α
sec (–α) = sec α	cosec (–α) = – cosec α

Свойства четности вытекают из симметричности точек P
a
и Р
—
a
(рис. 14) относительно оси х
.При такой симметрии ордината точки меняет знак ((х
; у
)переходит в (х
; –у)). Все функции – периодические, синус, косинус, секанс и косеканс имеют период 2p

,а тангенс и котангенс – p

sin (α + 2kπ ) = sin α	cos (α + 2kπ ) = cos α
tg (α + kπ ) = tg α	ctg (α + kπ ) = ctg α
sec (α + 2kπ ) = sec α	cosec (α + 2kπ ) = cosec α

Периодичность синуса и косинуса следует из того, что все точки P
a
+ 2 kp

, где k
= 0, ±1, ±2,…, совпадают, а периодичность тангенса и котангенса – из того, что точки P
a
+ kp

поочередно попадают в две диаметрально противоположные точки окружности, дающие одну и ту же точку на оси тангенсов.

Основные свойства тригонометрических функций могут быть сведены в таблицу:

Функция	Область определения	Множество значений	Четность	Участки монотонности (k = 0, ± 1, ± 2,…)
sin x	–Ґ x Ґ		нечетная	возрастает при x О ((4k – 1) p /2, (4k + 1) p /2),убывает при x О ((4k + 1) p /2, (4k + 3) p /2)
cos x	–Ґ x Ґ		четная	Возрастает приx О ((2k – 1) p , 2kp ),убывает приx О (2kp , (2k + 1) p )
tg x	x № p /2 + p k	(–Ґ , +Ґ )	нечетная	возрастает приx О ((2k – 1) p /2, (2k + 1) p /2)
ctg x	x № p k	(–Ґ , +Ґ )	нечетная	убывает приx О (kp , (k + 1) p )
sec x	x № p /2 + p k	(–Ґ , –1] И [+1, +Ґ )	четная	Возрастает приx О (2kp , (2k + 1) p ),убывает приx О ((2k – 1) p , 2kp )
cosec x	x № p k	(–Ґ , –1] И [+1, +Ґ )	нечетная	возрастает приx О ((4k + 1) p /2, (4k + 3) p /2),убывает приx О ((4k – 1) p /2, (4k + 1) p /2)

Способы определения

Геометрическое определение

Рис. 2Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически. Пусть нам данадекартова система координатна плоскости, и построена окружность радиусаRс центром в начале координатO. Измерим углы как повороты от положительного направления оси абсцисс до лучаOB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным. Абсциссу точкиВобозначимx_B, ординату обозначимy_B(см. рисунок).

Синусом называется отношение
Косинусом называется отношение
Тангенс определяется как
Котангенс определяется как
Секанс определяется как
Косеканс определяется как

Рис. 3Численные значения тригонометрических функций углаαв тригонометрической окружности с радиусом, равным единице

Ясно, что значения тригонометрических функций не зависят от величины радиуса окружностиRв силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординатеy_B, а косинус — абсциссеx_B. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

Еслиα —вещественное число, то синусомαв математическом анализе называется синус угла,радианнаямера которого равнаα, аналогично для прочих тригонометрических функций.

Определение тригонометрических функций для острых углов

Рис. 4Тригонометрические функции острого угла

Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. ПустьOAB — треугольник с угломα. Тогда:

Синусом углаαназывается отношениеAB/OB(отношение противолежащего катета к гипотенузе).
Косинусом углаαназывается отношениеОА/OB(отношение прилежащего катета к гипотенузе).
Тангенсом углаαназывается отношениеAB/OA(отношение противолежащего катета к прилежащему).
Котангенсом углаαназывается отношениеОА/AB(отношение прилежащего катета к противолежащему).
Секансом углаαназывается отношениеОB/OA(отношение гипотенузы к прилежащему катету).
Косекансом углаαназывается отношениеОB/AB(отношение гипотенузы к противолежащему катету).

Построив систему координат с началом в точкеO, направлением оси абсцисс вдольOAи в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.

Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см.:Теорема синусов,Теорема косинусов).

Определение тригонометрических функций как решений дифференциальных уравнений

Функциикосинусисинусможно определить какчётное(косинус) инечётное(синус) решениедифференциального уравнения

с начальными условиями, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:

Определение тригонометрических функций как решений функциональных уравнений

Функциикосинусисинусможно определить какнепрерывные решения(fиgсоответственно) системыфункциональных уравнений:

Определение тригонометрических функций через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу. Тогда можно воспользоваться теориейрядов Тейлораи представить синус и косинус в виде суммы степенны́х рядов:

Пользуясь этими формулами, а также уравнениямииможно найти разложения в ряд Тейлора и других тригонометрических функций:

где

B_n —числа Бернулли,

E_n —числа Эйлера.

Содержание

Формулы приведения для котангенса

Функция y = sin х.

Методы раскрытия скобок

Метод раскрытия одной пары скобок

Метод раскрытия нескольких пар скобок

Метод раскрытия квадратных скобок

Метод раскрытия фигурных скобок

Метод раскрытия скобок с использованием квадратного корня

Тангенс угла

Косинус в квадрате, синус в квадрате

Область применения

Преобразование произведения тригонометрических функций

Определение

Power series and Taylor series

Computation of power series

Taylor polynomials as approximations

Сферическая тригонометрия

Формулы суммы и разности тригонометрических функций

Differentiation

First derivative

Second derivative

Четность и периодичность.

Способы определения

Геометрическое определение

Определение тригонометрических функций для острых углов

Определение тригонометрических функций как решений дифференциальных уравнений

Определение тригонометрических функций как решений функциональных уравнений

Определение тригонометрических функций через ряды

Похожие записи:

Похожие записи: