Что значит перпендикулярный треугольник

Введение в перпендикуляр треугольника

Прежде чем углубляться в подробности, давайте разберемся, что такое перпендикулярные линии и почему они важны в геометрии. Перпендикулярные линии – это две линии, пересекающиеся под прямым углом, образующие угол 90 градусов. Это пересечение создает уникальные отношения между линиями и позволяет исследовать различные геометрические свойства.

Перпендикуляр треугольника относится к линиям или сегментам, которые перпендикулярны определенным компонентам треугольника, таким как его стороны, медианы или высоты

Эти перпендикуляры имеют важное математическое и практическое значение, что делает их решающими при изучении треугольников и их свойств

Проведение перпендикуляра из точки к прямой

В жизни с перпендикуляром можно столкнуться часто. Например, если по двум параллельным направляющим движутся тела, то кратчайшее расстояние между ними будет лежать именно по перпендикуляру.

Допустим, на уроке ученикам дали задание построить перпендикуляр к имеющейся площади. Особым условием является то, что проходить этот перпендикуляр должен через выбранную точку. Технически задача проста. Для ее исполнения нужен чертежный треугольник, один угол у которого является прямым, то есть составляет 90°.

Приложив его к прямой таким образом, что одна из сторон, образующих прямой угол, лежит на прямой, а другая — проходит через точку с определенными координатами, необходимо соединить эту точку и прямую.

Для перпендикуляра, проведенного из выбранной точки к прямой, можно определить длину. Она равна расстоянию от этой точки до точки пересечения с прямой плоскостью.

Условия, при которых равнобедренный треугольник прямоугольный

1. Угол при основании равнобедренного треугольника равен 90 градусам. Если у равнобедренного треугольника один из углов при основании равен 90 градусам, то такой треугольник будет являться прямоугольным. Если же угол при основании не равен 90 градусам, равнобедренный треугольник не будет прямоугольным.
2. Соотношение сторон. Также, равнобедренный треугольник может быть прямоугольным, если соотношение между его сторонами удовлетворяет определенному условию. В прямоугольном равнобедренном треугольнике, сторона, отличная от основания и равных сторон, будет являться гипотенузой. Поэтому, для того чтобы найти соотношение сторон равнобедренного прямоугольного треугольника, можно воспользоваться теоремой Пифагора. Если основание равнобедренного треугольника равно a, а сторона гипотенузы равно b, то такое треугольник будет прямоугольным, если выполнено условие: a^2 + a^2 = b^2.

Таким образом, равнобедренный треугольник может быть прямоугольным, если угол при основании равен 90 градусам или если стороны удовлетворяют условию теоремы Пифагора.

Существуют ли такие треугольники?

Существует всего лишь один способ, при котором равнобедренный треугольник может быть прямоугольным. Это возможно только в том случае, если две равные стороны имеют длину, равную квадратному корню из двух, а третья сторона равна двум.

В этом случае, прямой угол будет между двумя равными сторонами, и третья сторона будет выступать в качестве гипотенузы. Такой треугольник называется прямоугольно-равнобедренным.

Однако, стоит отметить, что прямоугольно-равнобедренные треугольники встречаются крайне редко в реальном мире. Они являются особым случаем и не являются типичными для равнобедренных треугольников. Большинство равнобедренных треугольников не являются прямоугольными.

Таким образом, можно сказать, что в общем случае равнобедренный треугольник не является прямоугольным, но существуют исключения, такие как прямоугольно-равнобедренные треугольники.

Методы расчета

Существует несколько методов для определения возможности существования прямоугольного треугольника и нахождения его сторон. Рассмотрим некоторые из них:

• Пифагорова теорема — один из наиболее известных методов определения возможности существования и нахождения сторон прямоугольного треугольника. Согласно этой теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Таким образом, если известны длины двух сторон, можно найти длину третьей стороны, применяя формулу: c = √(a² + b²), где c — гипотенуза, a и b — катеты.
• Формула полупериметра — этот метод позволяет найти длины сторон прямоугольного треугольника, если известны его площадь и полупериметр. Площадь треугольника равна произведению полупериметра на радикал из разности произведений полупериметра и длин каждой стороны (S = √(p(p-a)(p-b)(p-c))). Таким образом, зная площадь и полупериметр треугольника, можно найти длины его сторон.
• Формула радиуса вписанной окружности — если известен радиус вписанной окружности треугольника и его площадь, можно определить длины сторон прямоугольного треугольника. Формула для определения площади треугольника через радиус вписанной окружности имеет вид S = r * p, где S — площадь треугольника, r — радиус вписанной окружности, p — полупериметр треугольника. Таким образом, зная радиус вписанной окружности и площадь, можно определить длины сторон треугольника.

Это лишь некоторые методы определения возможности существования и нахождения сторон прямоугольного треугольника. В каждом конкретном случае необходимо выбрать наиболее подходящий метод и применить его для нахождения ответа.

Давайте рассмотрим пример применения этих методов. Пусть известна длина гипотенузы c и одного катета a прямоугольного треугольника, и необходимо найти длину второго катета и площадь треугольника.

Известные значения	Результаты
c = 5, a = 3	b = 4, S ≈ 6

Используя формулу Пифагора, можно найти длину второго катета:

b = √(5² — 3²) = √16 = 4

Далее, используя формулу для площади прямоугольного треугольника через полупериметр, можно найти площадь треугольника:

p = (3 + 4 + 5) / 2 = 6

S = √(6(6-3)(6-4)(6-5)) ≈ 6

Таким образом, длина второго катета равна 4, а площадь треугольника примерно равна 6.

Свойства серединного перпендикуляра к отрезку

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

АВ

Теорема

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство

Доказать: АМ = ВМ

Доказательство:

Доказать: N

m

Доказательство:

Рассмотрим произвольную точку N.

Если N

АВN Оm

Следствие 1

Геометрическим местом точек плоскости, равноудалённых от концов отрезка, является серединный перпендикуляр к этому отрезку.

Следствие2

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Теорема о трёх перпендикулярах

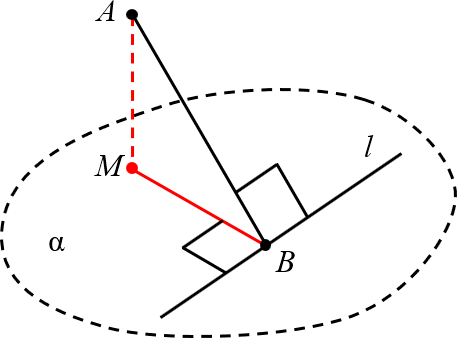
Из формулировки ясно, что теорема о трёх перпендикулярах работает при выполнении трёх обязательных условий:

1. Есть наклонная и есть проекция наклонной на плоскость $\alpha $;
2. Эта проекция (либо сама наклонная) перпендикулярна некой прямой $l$;
3. Прямая $l$ находится именно в плоскости $\alpha $.

Лишь в этом случае можно заявить, что наклонная (либо проекция) тоже перпендикулярна:

\

Убрать любое из этих трёх условий — и теорема не работает. Все дальнейшие рассуждения становятся необоснованными. Это особенно актуально на всевозможных экзаменах типа ЕГЭ и ДВИ, где недостаточно дать правильный ответ — нужно строгое обоснование каждого шага.

Рассмотрим простой пример:

Сравните два чертежа. Привычный для планиметрии «вид сверху»:

Без труда угадывается равнобедренный треугольник $ABC$ и дополнительное построение: Наклонная $MH$ и проекция $BH$.

А вот «вид сбоку», более типичный для стереометрии:

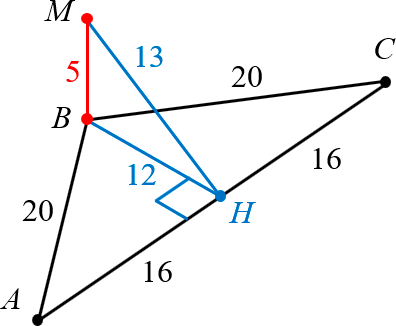
То же треугольник и те же дополнительные построения. Работать с таким чертежом большинству начинающих учеников гораздо сложнее. Поэтому смело используйте первый вариант. С опытом возьмёте на вооружение и второй.

Пример решения задачи

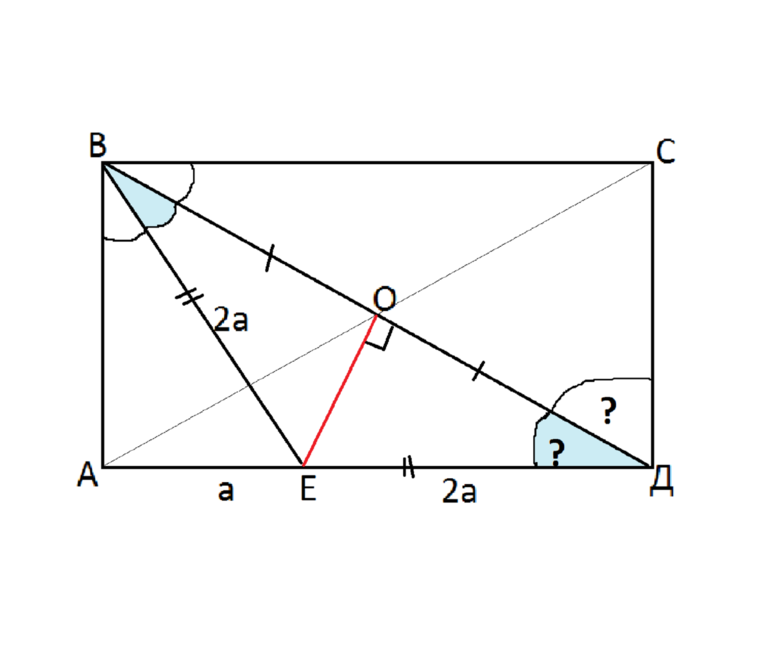
В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:

1. Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
2. Серединный перпендикуляр, проведенный к диагонали прямоугольника.
3. Точка Е делит сторону на отрезки а и 2а.

Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении

Рисунок 1. Чертеж для решения задачи.

Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:

Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
Необходимо найти угол ЕВО. Сделать это проблемно

Рекомендуется обратить внимание на треугольник АВЕ.
При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
Угол СВЕ вычисляется следующим образом: 90 — 30 = 60 (градусов).
Следовательно, искомый угол равен 30, поскольку 90 — 30 — 30 = 30.
В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).

Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой «х». Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = ^(1/2) = a * ^(1/2). Следовательно, АВ = a * ^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 — d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 — (d^2) / 4]^(1/2).

Прямоугольные треугольники

Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).

Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.

3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.

5. В равнобедренном прямоугольном треугольнике гипотенуза равна катету, умноженному на $√2$

6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$

7. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями, которых являются катеты данного треугольника.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.

6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.

7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	$/$	$/$	$/$
$cosα$	$/$	$/$	$/$
$tgα$	$/$	$1$	$√3$
$ctgα$	$√3$	$1$	$/$

Площадь прямоугольного треугольника равна половине произведения его катетов

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $АВ=10, АС=√$. Найдите косинус внешнего угла при вершине $В$.

Так как внешний угол $АВD$ при вершине $В$ и угол $АВС$ смежные, то

Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Следовательно, для угла $АВС$:

Катет $ВС$ мы можем найти по теореме Пифагора:

Подставим найденное значение в формулу косинуса

В треугольнике $АВС$ угол $С$ равен $90$ градусов, $sin⁡A=/, AC=9$. Найдите $АВ$.

Распишем синус угла $А$ по определению:

Так как мы знаем длину катета $АС$ и он не участвует в записи синуса угла $А$, то можем $ВС$ и $АВ$ взять за части $4х$ и $5х$ соответственно.

Применим теорему Пифагора, чтобы отыскать $«х»$

Так как длина $АВ$ составляет пять частей, то $3∙5=15$

В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:

Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.

В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.

Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.

Свойства перпендикулярных прямых

Сначала разберём два «стандартных» свойства, которые вы найдёте в любом учебнике геометрии 7-го класса. А затем — одно «нестандартное», но именно оно чаще всего и встречается в настоящих задачах.

3.1. Теорема о двух прямых, перпендикулярных третьей

Прямая $AB\bot EF$ и прямая $MN\bot EF$. Следовательно, прямые $AB$ и $MN$ не пересекаются. Проще говоря, они параллельны (см. урок «Параллельные прямые»).

3.2. Теорема о прямой, перпендикулярной данной

Доказательство этой теоремы состоит из двух частей: сначала докажем, что такую прямую провести можно, а затем — что она единственная.

Прямая, перпендикулярная данной, строится очень просто. Рассмотрим прямую $a$, на которой отмечена точка $M$:

Отложим от луча $MK$ угол, равный 90°. В любую сторону: в верхнюю полуплоскость или нижнюю — не имеет значения. Получим луч $MN$:

Наконец, продолжим луч $MN$ в противоположную другую сторону (т.е. построим дополнительный луч). Получим искомую прямую $MN\bot a$:

Единственность такого построения следует либо из аксиомы о том, что нужный угол можно отложить в нужном направлении одним и только одним способом, либо из предыдущей теоремы о двух прямых, перпендикулярных данной. В самом деле, пусть есть ещё одна прямая $ML$, которая, как и $MN$, перпендикулярна прямой $a$:

Поскольку $MN\bot a$ и $ML\bot a$, по предыдущей теореме эти прямые не пересекаются. Что противоречит нашему построению, в котором у прямых $MN$ и $ML$ есть общая точка $M$. Следовательно, прямые $MN$ и $ML$ совпадают, что и требовалось доказать.

3.3

Важное свойство прямого угла. Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах

Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:

Две теоремы, которые мы рассмотрели выше, редко встречаются в реальных примерах. Зато сейчас мы рассмотрим свойство, которое действительно помогает решать многие задачи. Звучит оно очень просто:

Это утверждение может показаться очевидным. И оно действительно является таковым. Однако деление прямого угла на части встречается в задачах настолько часто, что я не мог не упомянуть об этом.

Кроме того, начинающие ученики часто не замечают такие углы на чертежах. Поэтому сейчас мы будем отрабатывать эту теорему на реальных задачах.

Основные теоремы

Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.

Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:

• Прямая.
• Обратная.
• Пересечение в треугольнике.

Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.

Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.

Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.

Применение перпендикулярного треугольника

1. Архитектура и строительство: Перпендикулярные треугольники используются для построения прямых линий и определения перпендикулярных направлений при проектировании зданий и сооружений. Например, они помогают строителям создавать углы в 90 градусов и выравнивать стены и полы.
2. Картография: В картографии перпендикулярные треугольники используются для измерения и построения углов при создании карт и планов. Они позволяют прокладывать прямые линии и определять направления с большой точностью.
3. Инженерия: В инженерии перпендикулярные треугольники применяются для выравнивания и установки оборудования. Они помогают определить точные углы и направления, необходимые для правильной установки и функционирования различных систем и механизмов.
4. Геодезия: В геодезии перпендикулярные треугольники используются для измерения и построения прямых линий при определении географических координат и создании геодезических сетей.
5. Математика: В математике перпендикулярные треугольники раскрывают различные свойства и законы геометрии. Они являются базовым понятием в изучении теорем о прямых углах, прямых линиях и ортогональных направлениях.

Это лишь несколько примеров применения перпендикулярного треугольника. Это геометрическое понятие имеет широкий спектр применений и используется во многих областях науки, техники и дизайна.

Статьи о геометрии

Геометрия — раздел математики, изучающий фигуры, пространственные формы и их свойства. Это наука, которая помогает нам понять и анализировать мир вокруг нас, а также применяется во многих областях науки и техники.

В данном разделе вы найдете разнообразные статьи о геометрии, которые помогут вам расширить свои знания и понять различные аспекты этой науки.

Основные понятия геометрии

Перед тем, как начать изучение геометрии, следует ознакомиться с основными понятиями и определениями. Ниже приведен список статей, в которых рассматриваются основные геометрические термины:

1. Точка
2. Прямая
3. Отрезок
4. Угол
5. Треугольник
6. Четырехугольник
7. Окружность
8. Параллельные линии
9. Перпендикулярные линии

Свойства геометрических фигур

Каждая геометрическая фигура имеет свои особенности и свойства, которые помогают нам классифицировать их и разбираться в их характеристиках. В следующих статьях рассматриваются свойства различных фигур:

• Свойства треугольника
• Свойства прямоугольника
• Свойства квадрата
• Свойства круга
• Свойства параллелограмма
• Свойства ромба

Примеры задач

Решение геометрических задач требует применения знаний и навыков, полученных в процессе изучения геометрии. В данной статье представлены примеры задач, в которых требуется применить геометрические знания для их решения. Каждый пример сопровождается подробным объяснением решения:

• Расчет площади треугольника
• Нахождение периметра окружности
• Поиск угла между прямыми

Заключение

Геометрия — увлекательная наука, которая помогает нам разбираться в пространственных отношениях и формах. Статьи, представленные в данном разделе, помогут вам лучше понять и усвоить основы геометрии, а также применить их на практике при решении различных задач.

Формулы и свойства прямоугольного треугольника

Обозначения формул:

(см. рисунок выше)

a, b — катеты прямоугольного треугольника

c — гипотенуза

α, β — острые углы треугольника

S — площадь

h — высота, опущенная из вершины прямого угла на гипотенузу

m_a— медиана, проведенная к стороне a из противолежащего угла (α)

m_b — медиана, проведенная к стороне b из противолежащего угла (β)

m_c — медиана, проведенная к стороне c из противолежащего угла (γ)

В прямоугольном треугольнике любой из катетов меньше гипотенузы (Формулы 1 и 2). Данное свойство является следствием теоремы Пифагора.

Косинус любого из острых углов меньше единицы (Формулы 3 и 4). Данное свойство следует из предыдущего. Так как любой из катетов меньше гипотенузы, то из соотношение катета к гипотенузе всегда меньше единицы.

Квадрат гипотенузы равен сумме квадратов катетов (теорема Пифагора). (Формула 5). Это свойство постоянно используется при решении задач.

Площадь прямоугольного треугольника равна половине произведения катетов (Формула 6)

Сумма квадратов медиан к катетам, равна пяти квадратам медианы к гипотенузе и пяти квадратам гипотенузы, деленных на четыре (Формула 7). Кроме указанной, есть еще 5 формул, поэтому рекомендуется ознакомиться также и с уроком «Медиана прямоугольного треугольника», в котором более подробно изложены свойства медианы.

Высота прямоугольного треугольника равна произведению катетов, деленному на гипотенузу (Формула

Квадраты катетов обратно пропорциональны квадрату высоты, опущенной на гипотенузу (Формула 9). Данное тождество также является одним из следствий теоремы Пифагора.

Длина гипотенузы равна диаметру (двум радиусам) описанной окружности (Формула 10). Гипотенуза прямоугольного треугольника является диаметром описанной окружности. Это свойство часто используется при решении задач.

Радиус вписанной в прямоугольный треугольник окружности можно найти как половину от выражения, включающего в себя сумму катетов этого треугольника минус длину гипотенузы. Или как произведение катетов, деленное на сумму всех сторон (периметр) данного треугольника. (Формула 11) Синус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению противолежащего данному углу катета к гипотенузе (по определению синуса). (Формула 12). Данное свойство используется при решении задач. Зная величины сторон, можно найти угол, который они образуют.

Косинус угла А (α, альфа) в прямоугольном треугольнике будет равен отношению прилежащего данному углу катета к гипотенузе (по определению синуса). (Формула 13)

См. также Соотношения между углами и сторонами прямоугольного треугольника изучает Тригонометрия.

Содержание главы:

Прямоугольный треугольник

Биссектриса в прямоугольном треугольнике

Высота в прямоугольном треугольнике

Высота в прямоугольном треугольнике (Часть 2)

Теорема Пифагора и ее доказательство

Применение теоремы Пифагора

Гипотенуза прямоугольного треугольника

Перпендикуляр к плоскости прямоугольного треугольника

Подобие треугольников. Использование в задачахОписание курса Прямоугольный треугольник   

Важные свойства

Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:

В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.

Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:

Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:

Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.

Определение перпендикуляра

Перпендикуляр — это прямая, которая образует прямой угол со своими пересекающимися прямыми или плоскостями. Точка пересечения прямой и перпендикуляра называется точкой пересечения.

Особенности перпендикуляра:

• Угол между перпендикуляром и прямой равен 90 градусам (прямому углу).
• Перпендикулярные прямые или плоскости никогда не пересекаются.
• Перпендикулярные прямые или плоскости параллельны одна другой.

Свойства перпендикуляра:

1. Перпендикуляр к прямой, находящейся в плоскости, также лежит в этой плоскости.
2. Если две прямые перпендикулярны к одной и той же прямой, то они будут параллельны между собой.
3. Если прямая перпендикулярна к одной из прямых, параллельных друг другу, то она перпендикулярна и к другой прямой.

Примеры использования перпендикуляра:

• Построение прямоугольника: все стороны прямоугольника являются перпендикулярными к основному отрезку, то есть его диагонали.
• Строительство зданий: перпендикулярные стены и фасады зданий позволяют создать прямые углы и симметрию в строительстве.
• Геодезия и навигация: перпендикулярные линии используются для измерения углов и направлений при изучении местности и определении координат точек.

Особенности прямоугольного равнобедренного треугольника

Основные особенности прямоугольного равнобедренного треугольника:

1. Все три угла, образующие треугольник, суммируются в 180 градусов.
2. Один из углов является прямым углом (равным 90 градусам).
3. Две стороны, образующие прямой угол, равны друг другу.
4. Две другие стороны равны между собой.
5. Биссектриса (прямая, делящая угол пополам) одного из углов треугольника также является высотой (перпендикулярной стороне).
6. Определение площади треугольника можно упростить, так как высота и основание равнобедренного треугольника легко находятся.

Прямоугольный равнобедренный треугольник может быть использован в разных областях, например в конструировании и геометрии.

Математика. 3 класс

Конспект урока

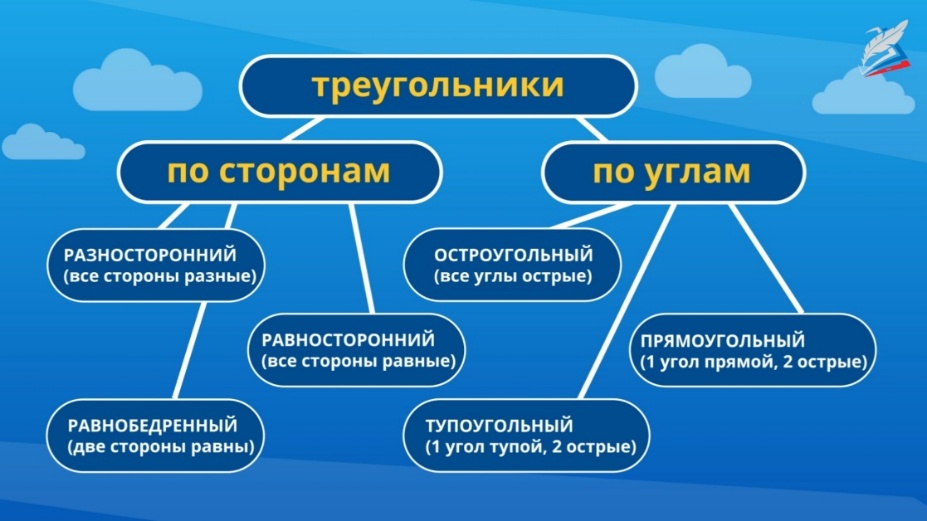
Виды треугольников по видам углов. Закрепление изученного материала

Перечень вопросов, рассматриваемых в теме:

Какие виды треугольников различают по видам углов?

Как различать треугольники: прямоугольный, тупоугольный, остроугольный?

Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.Треугольник – геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.

Виды треугольников по величине углов

Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.

Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.е. 90º.

Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.

Основная и дополнительная литература:

1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 85-87.

2. Волкова С. И. математика. Тесты. 3 кл. – М.: Просвещение, 2018. С. 60-67.

3. Рудницкая В. Н. Математика. Дидактические материалы. ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.

Теоретический материал для самостоятельного изучения

Давайте вспомним, что вы уже знаете о видах треугольников.

По длине сторон различают: разносторонние, равнобедренные и равносторонние треугольники.

Но было бы несправедливо разделить все треугольники на 3 вида по длине сторон. Ведь у каждого есть ещё и по три угла.

У вас уже появились идеи?

Острые – меньше прямого

Прямые – угол 90 градусов

Тупые – больше прямого

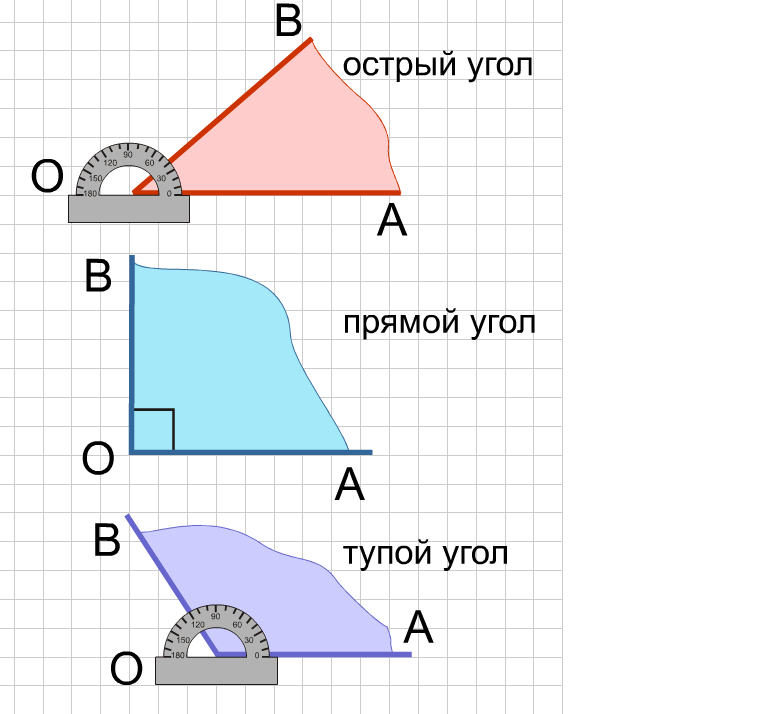
Оказывается, по величине углов все треугольники тоже можно разделить на 3 вида:

те, у которых все углы острые, – остроугольные,

те, у которых есть прямой угол, – прямоугольные,

те, у которых есть тупой угол, – тупоугольные.

Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира.

Обычно вид треугольника можно определить на глаз.

Попробуйте определить виды треугольников по величине углов без измерений.

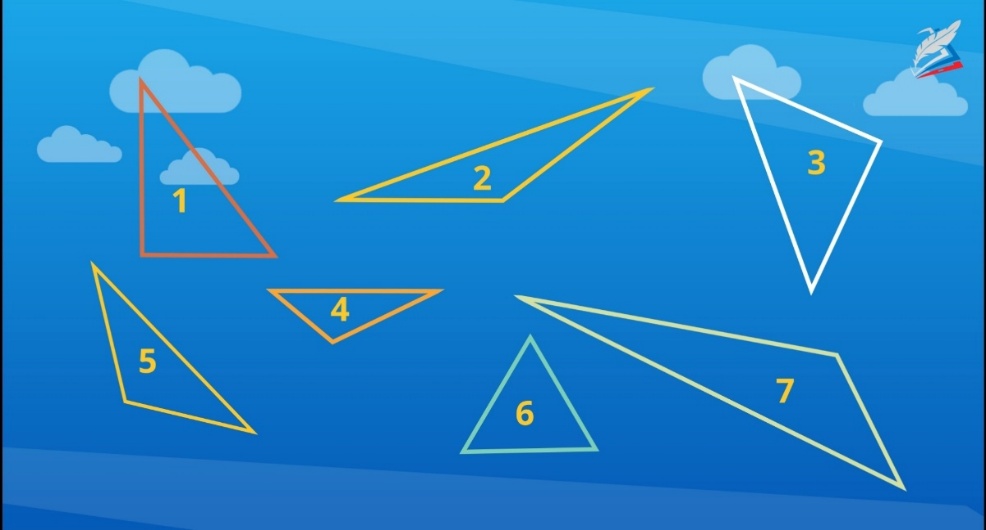
тупоугольный– 2, 4, 7, 5

По величине углов различают 3 вида треугольников:

Остроугольные, прямоугольные и тупоугольные

Определить вид треугольника можно тремя способами:

с помощью измерений, на глаз и по условным обозначениям.

Задания тренировочного модуля

Остроугольный треугольник – это треугольник, у которого ……………………

Прямоугольный треугольник – это треугольник, у которого есть ……………………

Тупоугольный треугольник – треугольник, все стороны которого есть ……………………

Правильные варианты ответов:

Остроугольный треугольник — это треугольник, у которого все углы острые.

Прямоугольный треугольник — это треугольник, у которого есть прямой угол.

Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.

Определите вид треугольника по величине углов и выпишите номера треугольников по порядку:

Использование перпендикуляра треугольника

Перпендикуляры треугольника играют важную роль в геометрии и имеют множество практических применений. Некоторые из важных областей, где используется перпендикуляр треугольника, включают:

Измерение высоты треугольника: Один из основных способов определения высоты треугольника — это построение перпендикуляра из вершины треугольника к противоположной стороне. Этот перпендикуляр будет служить вспомогательной линией для измерения высоты треугольника.
Построение перпендикулярного отрезка: Перпендикуляр треугольника может быть использован для построения перпендикулярного отрезка на плоскости. Для этого достаточно провести перпендикуляр из одной из вершин треугольника к его противоположной стороне.
Определение точки пересечения: Если два перпендикуляра проведены из двух разных вершин треугольника к противоположным сторонам, то они пересекутся в точке, которая может быть использована для различных геометрических конструкций.
Определение ортоцентра: Ортоцентр треугольника — это точка пересечения трех высот треугольника, которые являются перпендикулярами к сторонам треугольника

Эта точка имеет важное значение в геометрии и может быть использована, например, для построения окружности, проходящей через вершины треугольника.

Это лишь некоторые из многочисленных способов использования перпендикуляра треугольника. Знание и понимание свойств и применений перпендикуляра треугольника позволяют увидеть и использовать их в различных задачах геометрии и практических применениях в реальной жизни.