Сколько целых решений может иметь неравенство? понимаем смысл выражения

Основные правила решения линейных неравенств

Линейные неравенства можно записать в таком виде:

Здесь a и b являются какими-либо числами, при этом определяется, как неизвестная переменная.

Неравенства могут быть строгими, нестрогими и прочими.

Строгие неравенства, содержащие знаки больше (>) или меньше (<):

a < b — тогда a меньше по сравнению с b,

a > b — тогда a больше по сравнению с b,

a > b и b < a являются равносильными неравенствами, так как обозначают одно и тоже.

Нестрогие неравенства, содержащие знак сравнения (больше или равно) или (меньше или равно):

— тогда a меньше по сравнению с b, либо они равны,

— это значит, что a больше по сравнению с b, либо они равны,

знаки и противоположны друг другу.

Прочие неравенства:

— тогда a не равно b,

a \gg b — тогда a много больше по сравнению с b,

— тогда a много меньше по сравнению с b,

знаки являются противоположными друг другу.

Числовые неравенства характеризуются следующими свойствами:

При a > b имеем, что b < a. Справедливо и обратное утверждение: если a < b, тогда b > a.
При a > b и b > c верно, что a > c. С другой стороны, при a < b и b < c, то a < c.
Когда a > b, верно, что a + c > b + c (и a — c > b — c). При a < b верно, что a + c < b + c (и a — c < b — c). Обе части данного выражения допускается увеличить или уменьшить на одинаковую величину.
Когда a > b и c > d, верно, что a + c > b + d . При a < b и c < d, получим, что a + c < b + d. Если неравенства имеют один и тот же смысл, их можно суммировать, складывая соответствующие члены. В процессе требуется выполнить проверку. К примеру, когда из 12 > 8 почленно отнимают 3 > 2, получается правильный ответ 9 > 6. Если из 12 > 8 почленно отнять 7 > 2, то полученное выражение будет неверным.
При a > b и c < d получим, что a — c > b — d. Когда a < b и c > d, справедливо, что a — c < b — d. Из какого-либо неравенства допускается почленно отнимать другое неравенство которое противоположно первому по смыслу. Знак при этом сохранится того неравенства, которое играло роль уменьшаемого.
Если a > b, m является положительным числом, то получим, что ma > mb. Обе части неравенства допускается умножать и делить на одинаковое положительное число. Знак при этом сохраняется без изменений. В том случае, когда а > b, n является отрицательным числом, получим, что na < nb. Таким образом, обе части неравенства допустимо умножить или разделить на одно и то же отрицательное число. Здесь потребуется изменить знак полученного неравенства на противоположный.
Когда a > b и c > d, где a, b, c, d > 0 верно, что ac > bd. При a < b и c < d, где a, b, c, d > 0, получим, что ac < bd. Неравенства, которые обладают одинаковым смыслом, в пределах множества из положительных чисел допускается почленно умножать. Следствие рассмотренного свойства или квадратный пример: если a > b, где a, b > 0, то , и если a < b то . На множестве положительных чисел обе части можно возвести во вторую степень, то есть в квадрат.
В том случае, когда a > b, где a, b > 0, то . При a < b получим, что .

Поиск корней, или решений, неравенства можно значительно упростить. Для этого требуется выполнить преобразования, которые являются равносильными друг другу. В результате начальное неравенство будет записано в более простой форме. При этом имеющиеся решения сохраняются, а образование посторонних корней исключается.

Благодаря рассмотренным ранее свойствам неравенств, можно сформулировать несколько полезных правил, которые пригодятся для решения контрольных и задач по математике.

Значение множества натуральных решений для задач оптимизации

Оптимизационные задачи встречаются во многих областях, таких как экономика, инженерия, логистика и многие другие. Целью оптимизации является минимизация или максимизация определенной функциональной зависимости при заданных ограничениях. Множество натуральных решений позволяет определить, какие значения переменных необходимо рассматривать при поиске наилучшего решения.

Например, пусть у нас есть задача оптимизации, связанная с выбором оптимального количества производимых товаров, с учетом ограничений на себестоимость, спрос и доступные ресурсы. В этом случае множество натуральных решений будет определять, какое количество товаров следует производить для достижения оптимальной прибыли.

Множество натуральных решений также позволяет оценить эффективность различных алгоритмов оптимизации. Сравнение результатов, полученных на разных множествах натуральных решений, позволяет оценить, насколько каждый алгоритм способен находить оптимальное решение в разных условиях.

Пример	Описание
Задача о рюкзаке	Множество натуральных решений позволяет определить, какие предметы нужно положить в рюкзак, чтобы его вес не превышал заданного значения, а стоимость была максимальной.
Задача о транспортной логистике	Множество натуральных решений определяет оптимальное распределение грузов по маршрутам таким образом, чтобы затраты на топливо и время были минимальными.
Задача о портфеле инвестиций	Множество натуральных решений позволяет определить оптимальное соотношение различных активов в инвестиционном портфеле с целью максимизации доходности при заданных рисках.

Таким образом, множество натуральных решений является ключевым элементом в оптимизации и позволяет эффективно решать различные задачи, обеспечивая наилучшие результаты при заданных ограничениях.

Практическое применение доказательства неравенств

Доказательство верности неравенств при всех значениях x может быть полезным во многих областях практической деятельности. Неравенства широко используются в математике, физике, экономике, компьютерных науках и других научных и прикладных дисциплинах. Понимание и умение доказывать неравенства помогает в анализе данных, моделировании систем и принятии решений.

В экономике и финансовой аналитике доказательство неравенств может быть полезным при определении оптимальных решений и оценке результатов. Например, при анализе прибыли и затрат компании можно использовать доказательство неравенств для определения граничных значений, при которых она оказывается прибыльной или убыточной. Такое доказательство может помочь установить основные факторы, влияющие на экономическую эффективность.

В области компьютерных наук доказательство неравенств применяется для анализа сложности алгоритмов, определения времени выполнения программ и оценки ресурсов, необходимых для выполнения задач. Неравенства позволяют сравнивать и классифицировать различные алгоритмы по их эффективности и помогают выбрать наиболее оптимальное решение для конкретной задачи.

В физике и инженерии доказательство неравенств используется при моделировании физических систем и оценке их свойств. Например, при изучении движения тела можно использовать неравенства для анализа его скорости, ускорения и траектории. Также доказательство неравенств может быть полезно при определении границ значений физических величин или при проверке устойчивости системы.

В конечном счете, практическое применение доказательства неравенств связано с умением анализировать и оценивать различные величины и свойства объектов и систем. Доказательство неравенств помогает развивать логическое мышление, улучшает математическую образованность и способствует принятию обоснованных решений в различных областях деятельности.

Что такое неравенство и как его решать графически?

Графическое решение неравенства позволяет наглядно представить множество значений, удовлетворяющих данному неравенству, на числовой прямой. Для этого необходимо выполнить следующие шаги:

Записать неравенство в стандартной форме, где все члены находятся на одной стороне и все знаки неравенства направлены в одну сторону.
На числовой прямой выбрать точку начала отсчета и отметить на ней все числа, которые могут удовлетворять неравенству.
Используя стрелки или закрашивание, указать множество значений, удовлетворяющих неравенству, на числовой прямой.
Если неравенство содержит знак «больше» или «меньше», закончить график точкой соответствующей стрелке. Если неравенство содержит знак «больше или равно» или «меньше или равно», закончить график закрашенной точкой соответствующей стрелке.

Графическое решение неравенства позволяет наглядно представить множество значений, удовлетворяющих неравенству, и ориентироваться в его решении. Однако следует помнить, что графический метод не всегда является точным и требует проверки найденного решения аналитическим способом.

Пример:

Решим неравенство 2x + 3

1. Запишем неравенство в стандартной форме: 2x

2. На числовой прямой отметим точку 0 и отметим все значения х, которые удовлетворяют неравенству:

—————o——————

x = -1 x = 0 x = 1

3. Закрасим или укажем стрелкой множество значений, удовлетворяющих неравенству:

|—————o——————

x = -1 x = 0 x = 1

4. Так как неравенство содержит знак «меньше», закончим график точкой:

|—————o——————

x = -1 x = 0 x = 1 —->

Таким образом, решением данного неравенства будет множество всех чисел x, которые меньше 1.

Определение двойного неравенства

Двойное неравенство — это неравенство, которое состоит из двух отдельных неравенств, связанных между собой. Оно указывает на то, что рассматриваемая величина находится в определенном интервале значений.

Двойное неравенство записывается с использованием специальных математических символов. Обычно используются символы «» и символы между ними, такие как «=», чтобы указать направление неравенства.

Примеры двойных неравенств:

3
-2 > y > -10
-1 ≤ z ≤ 1

Первые два примера представляют неравенства, в которых переменная находится в определенном интервале. В третьем примере переменная находится включительно в интервале, что обозначается символом «≤».

Двойные неравенства используются во многих областях математики, включая алгебру, геометрию и анализ. Они играют важную роль при решении уравнений и систем неравенств, а также служат основой для определения интервалов, на которых выполняются определенные условия.

Практическое руководство по решению примеров и нахождению неравенств

Решение примеров и нахождение неравенств является важной частью математического образования. Знание этого навыка позволяет нам легко решать математические задачи, а также применять их в реальной жизни

Чтобы решать примеры, сначала необходимо определить тип задачи. Некоторые из самых распространенных типов примеров включают в себя простые арифметические операции, такие как сложение, вычитание, умножение и деление. Другие типы примеров могут включать алгебруические выражения, дроби или процентные задачи.

Когда тип задачи определен, можно приступать к самому решению. Следует убедиться, что все данные правильно записаны и ясно видны. Затем можно использовать соответствующий математический метод для решения примера. Например, для примеров с использованием дробей, может потребоваться найти общий знаменатель и выполнить операцию с долями. Для примеров с использованием алгебраических выражений, может потребоваться упростить выражение или найти значения переменных.

Неравенства требуют отдельного рассмотрения. Их решение основано на понимании отношения между числами и применении соответствующих правил

При решении неравенств важно помнить, что при переносе значения с одной стороны неравенства на другую, необходимо изменить направление знака

Чтобы успешно решать примеры и находить неравенства, необходима практика. Чем больше задач вы решаете, тем более легко и быстро вы будете справляться с ними. Постоянная тренировка поможет вам развить логическое мышление и математические навыки, что полезно не только в учебе, но и в повседневной жизни.

Почему неравенства не решают так же, как уравнения?

Пример 1

Решить уравнение:

Итак, нужно найти корни уравнения. Что можно сделать?

Вариант первый.

Зафиксировать область допустимых значений (ОДЗ) выражения: \( x-1 \ne 0; \; x+5 \ne 0. \)
Убедиться в том, что уравнение представляет собой равенство двух дробей и воспользоваться основным свойтвом пропорции — произведение крайних членов пропорции равно произведению её средних членов — в просторечии «перемножить крест накрест.»
\
Решить простое (без дробей) рациональное уравнение. Здесь после раскрытия скобок и приведения подобных членов оно сведется к квадратному.
Сверить полученные корни с ОДЗ и, отбросив лишние, сформировать ответ.

Вариант второй.

Привести к общему знаменателю

При этом неважно перенесены ли предварительно все члены уравнения в одну сторону или нет. Не забыть об ограниченности области допустимых значений выражения (написать ОДЗ).Отбросить общий знаменатель (одинаковые знаменатели в обеих частях равенства, если не переносили всё в одну сторону)

Решить упрощенное уравнение, проверить полученные корни на соответствие ОДЗ, написать ответ.

Вариант третий.

Перенести все члены уравнения в левую часть равенства и привести к общему знаменателю.
\
Затем, вспомнив о том, что дробь равна нулю, когда её числитель равен нулю, а знаменатель не равен нулю, записать и решать следующую равносильную систему:
\

Попробуйте всё это проделать самостоятельно для тренировки навыков решения дробно-рациональных уравнений. И убедитесь в том, что во всех трёх случаях будут получены одинаковые ответы.Для решения уравнений реального ЕГЭ вы можете выбрать любой из этих подходов, который вам придётся по душе.

Ответ:

Замечение:Отдельные ответы удобно записывать в фигурных скобках как элементы перечислимого множества, в отличие от интервалов (a;b) и отрезков , для обозначения которых используются круглые или квадратные скобки соответственно..

Пример 2

Решить неравенство:

Это неравенство содержит те же самые дробные выражения, что и предыдущее уравнение. Однако теперьварианты «крест накрест» и отбрасывание общего знаменателя НЕПРИМЕНИМЫ, потому что в знаменателе присутствуют неизвестные величины, а следовательно мы не знаем знаков множителей и не сможем корректно применять свойства неравенств. Особенно это касается свойства 5, которое требует изменить знак неравенства при умножении на отрицательное число. Поэтому при решении дробно-рационального неравенствасамое разумное действие — перенести все его члены в одну сторону и сравнивать итоговое выражение с нулем, т.е. применим способ аналогичный рассмотренному варианту 3 для уравнений.

Далее можем рассуждать так:
Фактически, здесь мы должны определить знак дробного выражения. То есть при каких значениях переменной результат деления является неположительным числом (отрицательным или нулём).
Очевидно, это будет тогда, когда знаки числителя и знаменателя не совпадают. Таким образом, нужно рассмотреть два случая: числитель дроби меньше либо равен нулю И знаменатель положителен (> 0) ИЛИ числитель дроби больше либо равен нулю И знаменатель отрицателен (

Это рассуждение приводит нас к совокупности двух систем неравенств

Обратите внимание, если в текст размышлений можно вставить союз «И», то это система, в которой выражения мы соединяем обычно фигурной скобкой «{«, если же можно вставить союз «ИЛИ», т.е. объединить несколько разных случаев, то это совокупность, обозначаемая квадратной скобкой «»

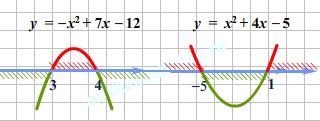
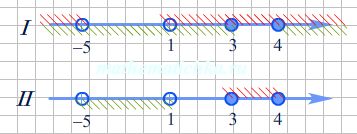
Ответ: .

Сравним ответ неравенства с ответом уравнения, рассмотренного выше. Значения переменной \(x = -5; x = 1; x = 3; x = 4 \) присутствовали как ключевые при решении уравнения, однако те из них, которые обращают знаменатель в 0, не вошли в ответ.
Но в ответе неравенства мы явно видим все эти значения переменной. Они фигурируют как границы промежутков. При этом входят или не входят граничные точки в ответ зависит от ОДЗ выражений и степени строгости неравенства.
Таким образом, наиболее частые ошибки при решении неравенств состоят в потере граничных точек и слиянии промежутков.

Методы доказательства неравенств

В математике существует несколько методов, которые позволяют доказывать различные типы неравенств. Вот некоторые из них:

Метод замены переменной: Данный метод заключается в том, чтобы заменить одну переменную на другую, таким образом, чтобы неравенство преобразовалось в более простую форму. Например, можно заменить переменную на выражение, которое гарантированно больше или меньше.
Метод математической индукции: Данный метод применяется для доказательства неравенств, которые верны для натуральных чисел. Он основан на идее, что если некое неравенство верно для одного натурального числа, и из этого следует, что оно верно и для следующего числа, то оно верно для всех натуральных чисел.
Метод доказательства по контрпримеру: В этом методе предлагается найти контрпример, то есть набор значений переменных, для которого неравенство не выполняется. Если контрпример найден, то неравенство неверно. Если же контрпример не найден, то неравенство может быть верным.
Метод монотонности: Этот метод применим, если известно, что функция или выражение монотонно возрастает или убывает на определенном интервале. В этом случае можно сравнить значения функции или выражения на границах интервала и сделать вывод о значении внутри интервала.

Все эти методы могут быть использованы для доказательства различных типов неравенств, включая линейные и квадратные неравенства, неравенства с модулем, треугольные неравенства и многие другие.

При выборе метода доказательства неравенства важно учитывать его особенности и свойства. Также полезно знать различные приемы и трюки, которые помогут упростить доказательство и получить более точный результат

Числовые неравенства

Вы умеете сравнивать целые числа, десятичные дроби. Знаете правила сравнения обыкновенных дробей с одинаковыми знаменателями, но разными числителями; с одинаковыми числителями, но разными знаменателями. Здесь вы научитесь сравнивать любые два числа с помощью нахождения знака их разности.

Сравнение чисел широко применяется на практике. Например, экономист сравнивает плановые показатели с фактическими, врач сравнивает температуру больного с нормальной, токарь сравнивает размеры вытачиваемой детали с эталоном. Во всех таких случаях сравниваются некоторые числа. В результате сравнения чисел возникают числовые неравенства.

Определение. Число а больше числа b, если разность а-b положительна. Число а меньше числа b, если разность а-b отрицательна.

Если а больше b, то пишут: а > b; если а меньше b, то пишут: а b означает, что разность а – b положительна, т.е. а – b > 0. Неравенство а b, a = b, a , = или b и b > с, то а > с.

Теорема. Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится. Следствие. Любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный.

Теорема. Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный. Следствие. Если обе части неравенства разделить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства разделить на одно и то же отрицательное число, то знак неравенства изменится на противоположный.

Вы знаете, что числовые равенства можно почленно складывать и умножать. Далее вы научитесь выполнять аналогичные действия с неравенствами. Умения почленно складывать и умножать неравенства часто применяются на практике. Эти действия помогают решать задачи оценивания и сравнения значений выражений.

При решении различных задач часто приходится складывать или умножать почленно левые и правые части неравенств. При этом иногда говорят, что неравенства складываются или умножаются. Например, если турист прошёл в первый день более 20 км, а во второй – более 25 км, то можно утверждать, что за два дня он прошёл более 45 км. Точно так же если длина прямоугольника меньше 13 см, а ширина меньше 5 см, то можно утверждать, что площадь этого прямоугольника меньше 65 см2.

При рассмотрении этих примеров применялись следующие теоремы о сложении и умножении неравенств:

Теорема. При сложении неравенств одинакового знака получается неравенство того же знака: если а > b и c > d, то a + c > b + d.

Теорема. При умножении неравенств одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака: если а > b, c > d и а, b, с, d – положительные числа, то ac > bd.

Неравенства со знаком > (больше) и 1/2, 3/4 b, c и и b, quad ax

НЕРАВЕНСТВО

— отношение, связывающее два числа

Иногда несколько Н. записываются вместе, напр.

Н., в к-рые входят величины, принимающие различные числовые значения, могут быть верны для одних значений этих величин и неверны для других. Так, неравенство

х,

Ниже приводятся нек-рые Н., выполняющиеся тождественно в той или иной области изменения входящих в них переменных.

1) Неравенство для модулей. Для любых действительных или комплексных чисел

. 2) Неравенство для средних. Наиболее известны Н., связывающие гармоническое, геометрическое, арифметическое и квадратичное средние:

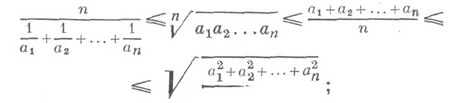
здесь все числа

3) Неравенства для сумм и их интегральные аналоги. Таковы, напр., Вуняковского неравенство, Гёльдера неравенство, Гильберта неравенство, Коши неравенство.

4) Неравенства для степеней чисел. Наиболее известно здесь Минковского неравенство и его обобщения на случай рядов и интегралов.

5) Неравенства для некоторых классов последовательностей и функций. Примерами могут служить Чебышева неравенство для монотонных последовательностей и Иенсена неравенство для выпуклых функций.

7) Линейные неравенства. Рассматривается система Н. вида

Совокупность решений этой системы Н. представляет собой нек-рый выпуклый многогранник в n-мерном пространстве (

линейных неравенств

Лит.:Харди Г. Г., Литтльвуд Д ж. Е., Полиа Г., Неравенства, пер. с англ., М., 1948; Беккен6ах Э., Беллмав Р., Неравенства, пер. с англ., М., 1965.

По материалам одноименной статьи из БСЭ-3.

Метод интервалов

Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

Метод интервалов заключается в следующем:

вводим функцию y = ax + b;
ищем нули для разбиения области определения на промежутки;
отмечаем полученные корни на координатной прямой;
определяем знаки и отмечаем их на интервалах.

Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:

найдем нули функции y = ax + b для решения уравнения ax + b = 0.

Если a ≠ 0, тогда решением будет единственный корень — х₀;

начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
определим знаки функции y = ax + b на промежутках.

Для этого найдем значения функции в точках на промежутке;

если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.

Как решаем:

В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

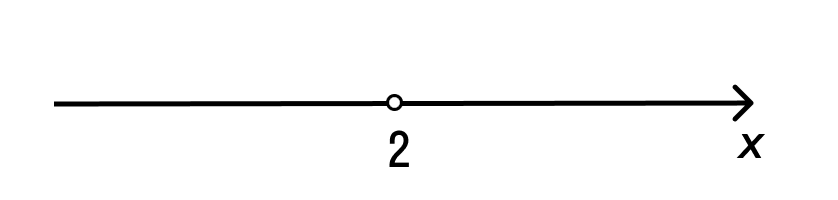
Определим знаки на промежутках.

Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6

Методы доказательства убывания функции

Метод дифференцирования. Один из наиболее распространенных методов доказательства убывания функции заключается в применении теоремы Ферма и теоремы Ролля. С помощью дифференцирования и анализа знаков производной функции можно показать, что функция является убывающей на заданном интервале.
Метод применения неравенств. Третий метод заключается в использовании различных неравенств для доказательства убывания функции. Например, можно воспользоваться неравенством Коши или неравенством между арифметическим и гармоническим средним.
Метод математической индукции. В некоторых случаях, для доказательства убывания функции можно использовать метод математической индукции. Он заключается в проверке базового шага и индуктивного предположения, а затем в доказательстве шага индукции, позволяющего заключить о убывании функции на всем интервале.

Каждый из этих методов имеет свои особенности и применяется в зависимости от сложности задачи и доступных инструментов для доказательства. При решении задач по убыванию функций рекомендуется использовать комбинацию различных методов для достижения наиболее точных результатов.

Применение целочисленных решений в математике

Целочисленные решения неравенств играют важную роль в различных областях математики и ее приложениях. Они позволяют определить диапазон значений переменных, при которых неравенство выполняется.

Прежде чем рассмотреть конкретные примеры применения целочисленных решений, давайте вспомним основные понятия. Целочисленные решения неравенства — это значения переменных, которые являются целыми числами и удовлетворяют заданному неравенству. Например, в неравенстве x

Одним из важных примеров применения целочисленных решений является задача оборудования дома. Предположим, что у нас есть квартира с определенным количеством комнат и нужно выбрать подходящий набор мебели для каждой комнаты. Если мы хотим, чтобы наборы мебели были одинаковыми и не использовать одну и ту же мебель более одного раза, то целочисленные решения неравенств позволят нам определить количество различных вариантов выбора мебели.

Еще одним примером применения целочисленных решений является задача расположения студентов в общежитии. Если у нас есть ограниченное количество комнат и мы хотим распределить студентов так, чтобы в каждой комнате было одинаковое количество студентов, целочисленные решения помогут нам определить максимальное количество студентов, которое можно разместить в общежитии.

Также целочисленные решения широко используются в оптимизационных задачах. Например, при планировании производства или распределении ресурсов, необходимо найти оптимальное количество товаров или ресурсов, которое удовлетворяет заданным ограничениям и минимизирует затраты.

В заключение, целочисленные решения неравенств играют важную роль в математике, экономике, инженерии и других областях. Они позволяют нам определить допустимые значения переменных и найти оптимальные решения задач. Понимание применения целочисленных решений помогает в решении практических задач и принятии важных решений.

Целые числа

Целые числа – это числа, которые не имеют дробной части, т.е. являются натуральными числами, нулем и отрицательными натуральными числами.

Целые числа используются в математике, физике, программировании и других научных дисциплинах для описания количественных значений и расчетов.

Свойства целых чисел

Сложение: сумма двух целых чисел всегда является целым числом.
Умножение: произведение двух целых чисел всегда является целым числом.
Деление: при делении одного целого числа на другое результат может быть как целым, так и дробным числом.
Остаток: при делении одного целого числа на другое всегда получается остаток, который также является целым числом.

Примеры использования целых чисел в математике и программировании

В математике целые числа используются для решения уравнений, поиска наибольшего общего делителя, определения простых чисел и многих других задач. В программировании целые числа используются для хранения и обработки данных, таких как возраст, количество товаров на складе, сумма платежей и других числовых значений.

Заключение

Целые числа являются важным элементом математики и науки, позволяя описывать и анализировать количественные значения. Понимание свойств и применения целых чисел позволяет решать многие задачи и производить точные расчеты.

Важность изучения неравенств для науки и образования

В науке неравенства играют особую роль в областях, таких как физика, химия, экономика и теория вероятностей. Они помогают устанавливать границы и ограничения для физических и химических процессов, определять зависимости между различными переменными и оценивать вероятности событий.

В образовании изучение неравенств развивает умение анализировать и сравнивать числовую информацию, формулировать и доказывать математические утверждения и решать сложные задачи. Оно также способствует развитию логического мышления и способности применять математические методы в повседневной жизни.

Изучение неравенств помогает студентам развить навыки рационального мышления, принятия решений и критического анализа. Оно учит логической строгости мышления, построению доказательств, а также помогает развить математическую интуицию и креативность.

Кроме того, изучение неравенств имеет практическое применение во многих областях жизни, включая экономику, финансы, статистику и инженерию. Оно позволяет решать задачи оптимизации, устанавливать условия безопасности и эффективности, а также проводить анализ данных и прогнозирование.

Изучение неравенств является неотъемлемой частью математического образования и науки.
Неравенства помогают сравнивать числа и выражения и находят применение в различных областях знаний.
Изучение неравенств развивает умение анализировать и сравнивать информацию, формулировать и доказывать утверждения и решать сложные задачи.
Изучение неравенств помогает развить навыки рационального мышления, принятия решений и критического анализа.
Неравенства имеют практическое применение в экономике, финансах, статистике и инженерии.

Определение количества целочисленных решений неравенств: основные принципы и методы

Определение количества целочисленных решений неравенств является важной задачей в алгебре и математическом анализе. Эта задача заключается в нахождении всех целых чисел, которые удовлетворяют некоторому неравенству

Количество таких целочисленных решений может быть разным в зависимости от вида неравенства и конкретных ограничений.

Существует несколько основных принципов и методов, которые позволяют определить количество целочисленных решений неравенств:

Метод перебора: этот метод заключается в переборе всех возможных значений целых чисел в заданном диапазоне и проверке их удовлетворения неравенству. Хотя этот метод может быть эффективен для небольших значений, он становится неэффективным при больших ограничениях или сложных неравенствах.
Использование математических свойств и теорем: в некоторых случаях можно использовать известные математические свойства и теоремы для определения количества целочисленных решений. Например, если неравенство является линейным или квадратичным, можно использовать методы алгебры для нахождения всех решений.
Анализ графика функции: графический метод позволяет визуализировать неравенство и определить область, в которой находятся целочисленные решения. Для этого строится график функции, соответствующей неравенству, и анализируется его поведение на целых числах.
Использование теории делимости: теория делимости позволяет выполнять различные операции с числами и применять различные алгоритмы для определения наличия целочисленных решений неравенств. Например, можно использовать разложение чисел на простые множители или алгоритм Евклида для нахождения наибольшего общего делителя.

Количество целочисленных решений неравенств может быть разным и зависит от типа неравенства, ограничений и специфических условий

Важно правильно выбрать метод и применить соответствующие математические инструменты для решения данной задачи

В заключение, определение количества целочисленных решений неравенств является сложной задачей, требующей применения различных принципов и методов. Правильный выбор метода и использование математического аппарата позволяют найти все целочисленные решения и получить точный ответ на поставленную задачу.

Понимание числовых неравенств: обе части имеют значение

Числовые неравенства представляют собой математические выражения, которые сравнивают два числа или выражения и указывают, какое из них больше или меньше. В некоторых случаях обе части неравенства могут иметь значение и могут быть использованы для нахождения диапазона допустимых решений.

Неравенства с двумя переменными представляют собой набор значений из областей переменных, где оба выражения неравны между собой. Например, неравенство x — 3 < 7 может быть записано в виде x < 10, что означает, что значение переменной x должно быть меньше 10.

Существует несколько методов решения числовых неравенств. Один из них — использование алгебраических операций, чтобы выразить переменную и определить, в каком диапазоне лежит значение. Этот метод может применяться как к одиночным неравенствам, так и к системам неравенств.

Решая числовые неравенства, необходимо учитывать знаки операций и правила алгебры. Например, при умножении или делении обе части неравенства на отрицательное число, необходимо изменить знак неравенства. Кроме того, при суммировании или вычитании чисел с переменной, нужно учитывать их знаки, чтобы определить диапазон возможных решений.

Понимание числовых неравенств, когда обе части имеют значение, является ключевым элементом в решении сложных математических задач. Оно позволяет определить допустимые значения переменных и найти решения, удовлетворяющие неравенствам. Эти навыки являются основой для решения множества математических и научных проблем, а также имеют широкое применение в реальном мире, включая экономику, физику и другие области.